Python-線形回帰
これは走っているキーボードマンの184番目の記事です
著者|私は走っているキーボードマンです
ソース|実行中のキーボードヒーロー(ID:runningkeyboardhero)
再印刷については、承認機関にお問い合わせください(WeChat ID:ctwott)
長い間投げた後でも、興味のある友達への参照用であれ、自分自身の学習や理解を深めるためであれ、何かを記録する必要があると感じています。
しかし、私は長い間このトピックについて考えていました。私は専門家の方向で深い学習をしており、現在は機械学習をかじっています。線形回帰を滑らかにする前に、1か月以上苦しんでいます。
このシリーズをPythonに入れるだけです。
もちろん、このセクションの内容は高エネルギーでなければなりません! ! !
とにかく、今月の時間は、aを勉強するのに1週間、bを勉強するのに1週間、そしてプロセス全体をスムーズにするために少し時間がかかります...
基本的なコンテンツは直接リンクされています:
Python-matplotlib描画(迷惑なメモではありません)
Chenkc、公開番号:AIマシン学習およびディープラーニングアルゴリズム[matplotlibを使用した簡単な描画](http://mp.weixin.qq.com/s?__biz=Mzg5NzE1NzM4NA==&mid=2247484802&idx=1&sn=c57b5913d82b743b8d386484de25058e&chksm=c07755e5f700dcf38230415c902df49c33ec48e1feac222902f59083177537b99f5f23edb40b#rd)
リンクを知っているhttps://www.zhihu.com/collection/260736383
深遠なことを簡単な方法で説明してください-勾配降下法とその実装、短い本のリンク:https://www.jianshu.com/p/c7e642877b0e
前の2つのフォアシャドウイングを使用すると、コードを直接アップロードできます
#! /usr/bin/env python3.6
# - *- coding: utf-8-*-
# @ Time :2020-11-0712:22
# @ Author : Ed Frey
# @ File : linear_regression.py
# @ Software: PyCharm
import matplotlib.pyplot as plt
import numpy as np
m =20
X0 = np.ones((m,1))
X1 = np.arange(1, m +1).reshape(m,1)
X = np.hstack((X0, X1))
y = np.array([3,4,5,5,2,4,7,8,11,8,12,11,13,13,16,17,18,17,19,21]).reshape(m,1)
xx = X1.reshape(1, m)[0]
yy = y.reshape(1, m)[0]
fig = plt.figure(figsize=(12,10), dpi=80)
plt.ion()
alpha =0.01
def error_function(theta, X, y):
diff = np.dot(X, theta)- y
return(1./2* m)* np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
diff = np.dot(X, theta)- y
return(1./ m)* np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
theta = np.array([1,1]).reshape(2,1)
gradient =gradient_function(theta, X, y)
i =0
items =[]while not np.all(np.absolute(gradient)<=1e-5):
theta = theta - alpha * gradient
gradient =gradient_function(theta, X, y)
u = np.linspace(-1,22,20)
v = theta[0][0]+ theta[1][0]* u
i +=1if i %1000==1:
items.append(theta)
items.append(theta)
j =0for theta in items:
plt.cla()
j +=1
plt.title("linear %s"%j)
plt.scatter(xx, yy)
plt.grid(True)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.xlim(-2,30,20)
plt.ylim(-2,30,20)
u0 =20
v0 = theta[0][0]+ theta[1][0]* u0
plt.plot(u, v, linewidth=3.0, color='r')
plt.annotate(r'$%f*u + %f = v$'%(theta[1][0], theta[0][0]), xy=(u0, v0), xycoords='data',
xytext=(-200,20), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle='->', connectionstyle='arc3,rad=.2'))
plt.savefig(fname="scatter%s.png"%j)
plt.pause(1)return theta
plt.ioff()
plt.show()
optimal =gradient_descent(X, y, alpha)print('optimal:', optimal)print('error function:',error_function(optimal, X, y)[0,0])
コードはあまり説明されておらず、基本的には短い本からコピーされており、上記の説明は十分に詳細です。初心者にはなじみのないのは、2つのN * 1次元行列aとbなどの行列と座標の表現です。座標に変換された後、横軸はすべてaになり、縦座標はすべてbになります。勾配降下法に関しては、それは数学的分析の基本的な部分です。さらに、それはマトリックス操作の少しの知識を含みます、そして私はその時に小さなカードを手に入れました。
後の描画部分のコードは、自分で補足・設計します。基本的な機能は、ターゲットの最適解を繰り返し検索する過程で、現在の解の効果を視覚化することです。つまり、グラフを通して現在のパラメータに対応する線形効果を確認できます。
出力のいくつかのレンダリングを傍受しました:
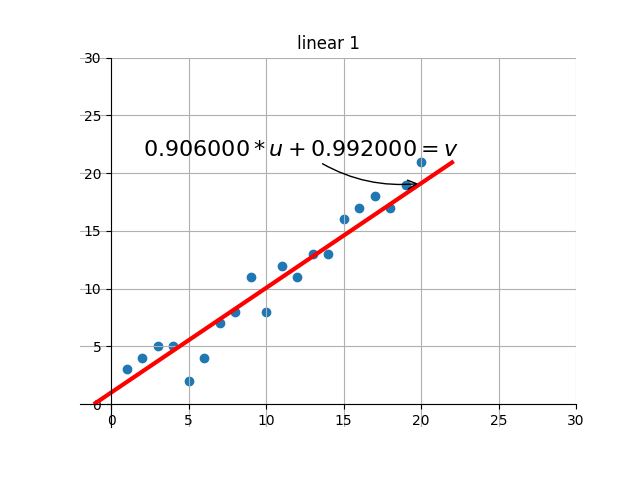
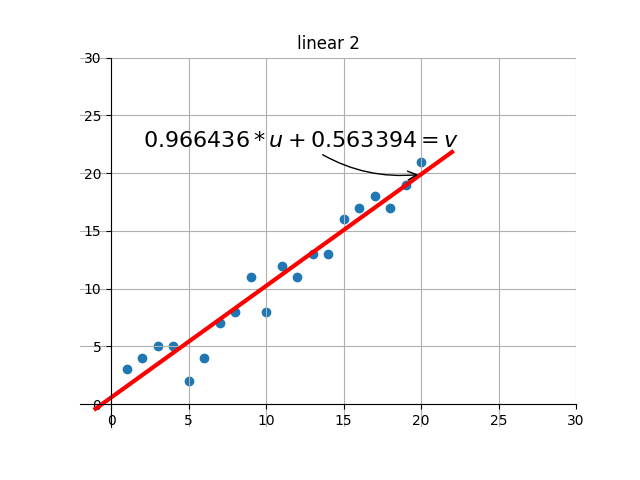
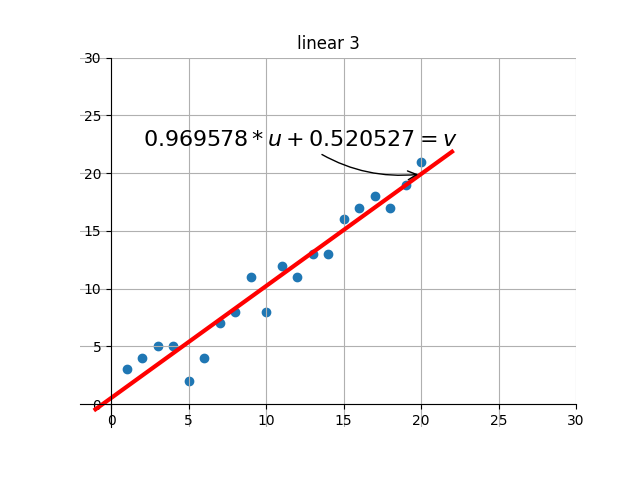
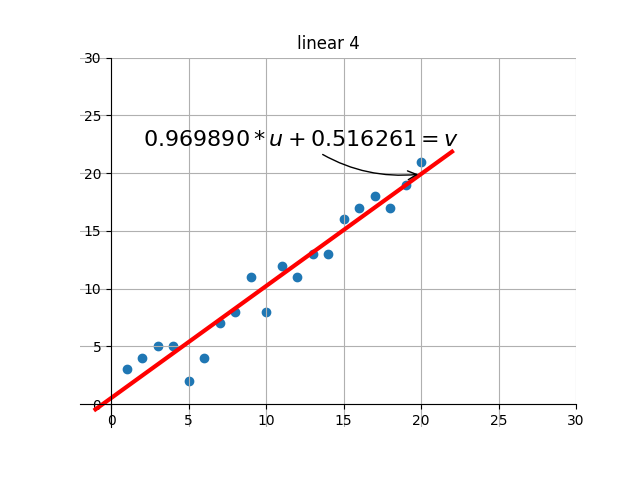
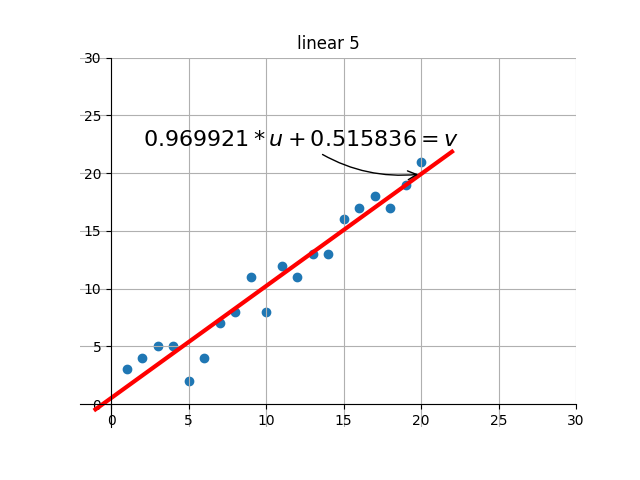
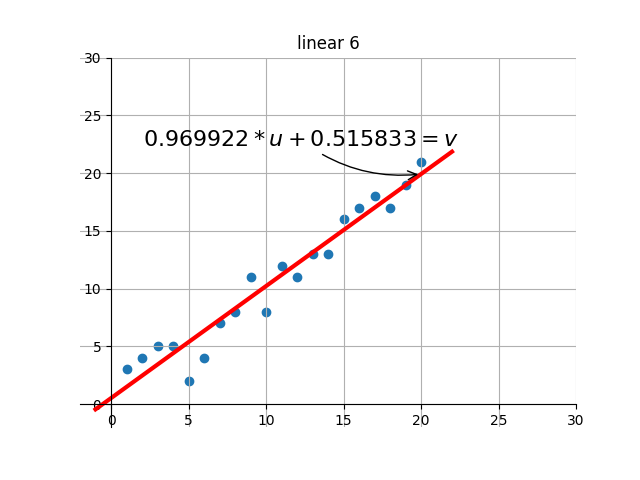
何?感じませんでしたか?別のアニメーションをしましょう

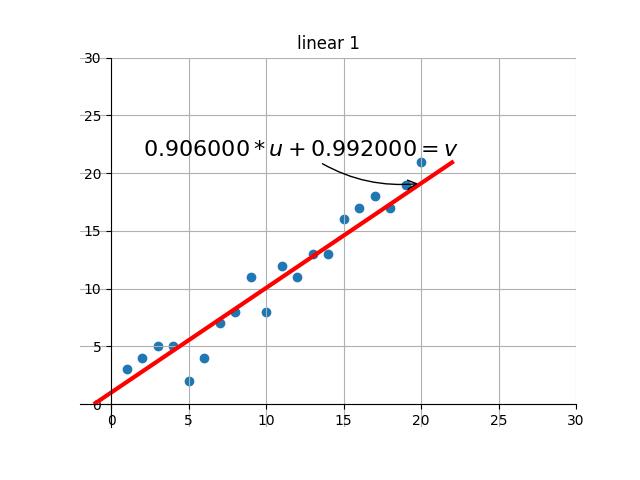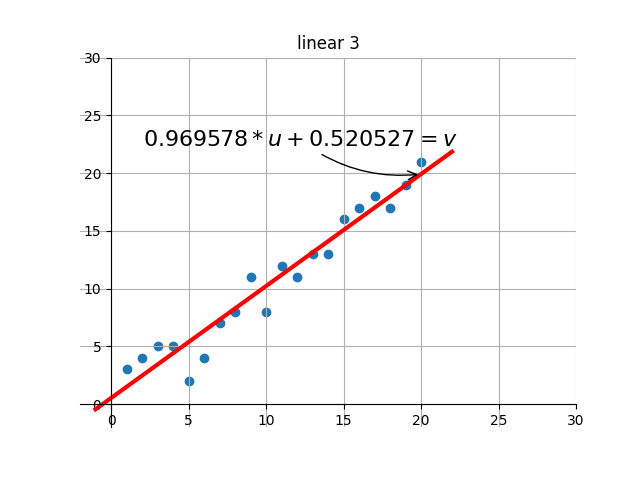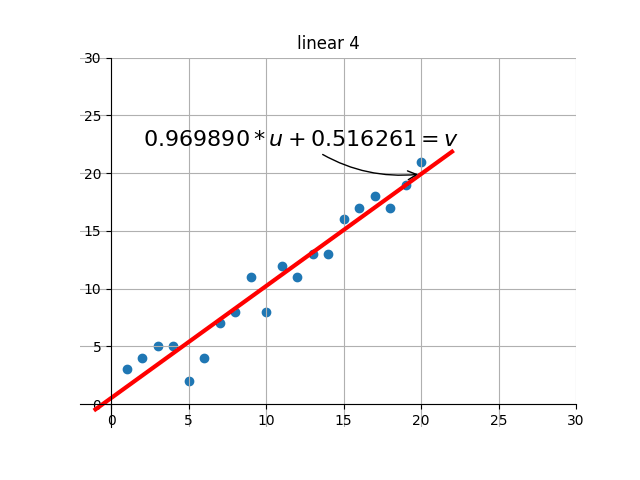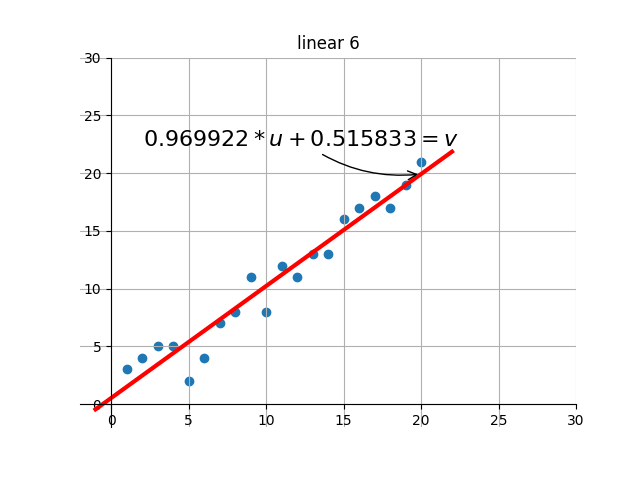
- END-
Recommended Posts