Pythonを使用したハイパーパラメータの最適化

この記事に添付されているコードはここにあります。

https://github.com/NMZivkovic/ml_optimizers_pt3_hyperparameter_optimization

これまで、機械学習を学習するプロセス全体で、いくつかの主要なトピックが取り上げられてきました。いくつかの回帰アルゴリズム、分類アルゴリズム、および2種類の問題（SVM、決定ツリー、ランダムフォレスト）に使用できるアルゴリズムを調査しました。さらに、私は監視されていない学習に足を踏み入れ、このタイプの学習をクラスタリングに使用する方法を学び、いくつかのクラスタリング手法について学びました。これらすべての記事では、Pythonを使用して「ゼロから」実装し、TensorFlow、Pytorch、SciKitLearnなどのライブラリを実装しています。

AIがあなたの仕事を引き継ぐのではないかと心配ですか？それを作った人であることを確認してください。上昇するAI業界との関連性を維持してください！

ハイパーパラメータは、すべての機械学習および深層学習アルゴリズムの不可欠な部分です。アルゴリズム自体によって学習される標準の機械学習パラメーター（線形回帰のwとb、ニューラルネットワークの接続の重みなど）とは異なり、エンジニアはトレーニングプロセスの前にハイパーパラメーターを設定します。これらは、エンジニアによって完全に定義された学習アルゴリズムの動作を制御する外部要因です。いくつかの例が必要ですか？

学習率は最も有名なハイパーパラメータの1つです。CはSVMのハイパーパラメータでもあります。決定ツリーの最大深度はハイパーパラメータなどです。これらはエンジニアが手動で設定できます。ただし、複数のテストを実行する場合は、面倒な場合があります。ここでハイパーパラメータ最適化が使用されます。これらの手法の主な目標は、検証セットで測定された最高のパフォーマンスを提供できる、特定のマシン学習アルゴリズムのハイパーパラメーターを見つけることです。このチュートリアルでは、最適なハイパーパラメータを提供できるいくつかの手法について説明します。

データセットと前提条件

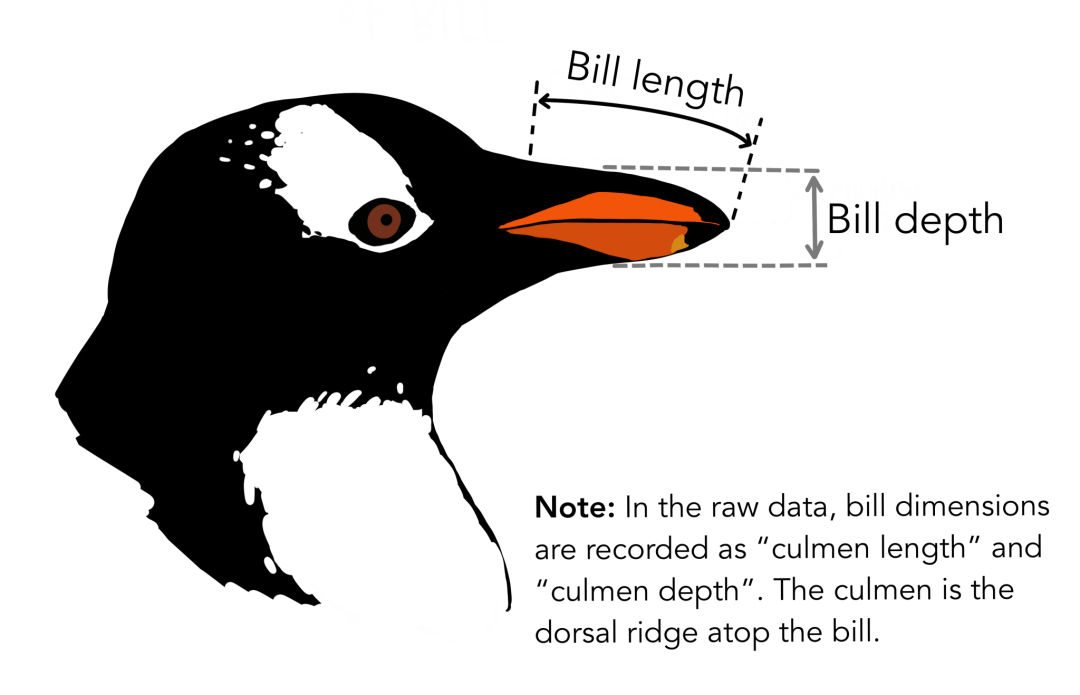
この記事で使用されているデータは、PalmerPenguinsデータセットからのものです。このデータセットは、有名なアイリスデータセットを置き換えるために最近導入されました。それは、南極のクリステン・ゴーマン博士とパーマー・ステーションによって作成されました。このデータセットは、ここまたはKaggleから入手できます。このデータセットは基本的に2つのデータセットで構成され、各データセットには344個のペンギンのデータが含まれています。アイリスデータセットと同様に、パーマー諸島の3つの島には3つの異なるペンギンがあります。繰り返しますが、これらのデータセットには各種の標本寸法が含まれています。高い門はくちばしの上部の尾根です。簡略化されたペンギンデータでは、頂点の長さと深さがculmen_length_mm変数とculmen_depth_mm変数に名前が変更されています。

https://github.com/allisonhorst/palmerpenguins

データセットにはラベルが付けられているため、実験結果を検証できます。しかし、これは通常は当てはまらず、クラスタリングアルゴリズムの結果の検証は通常、困難で複雑なプロセスです。

この記事では、次のPythonライブラリがインストールされていることを確認してください。

NumPy
SciKit学習
SciPy
Sci-Kitの最適化

インストールが完了したら、このチュートリアルで使用する必要なモジュールがすべてインポートされていることを確認してください。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

from sklearn.model_selection import GridSearchCV, RandomizedSearchCV

from sklearn.svm import SVC
from sklearn.ensemble import RandomForestRegressor

from scipy import stats
from skopt import BayesSearchCV
from skopt.space import Real, Categorical

さらに、少なくとも線形代数、計算、および確率の基本に精通している。

データを準備する

PalmerPenguinsデータセットをロードして準備します。最初にデータセットをロードし、この記事の未使用の関数を削除します。

data = pd.read_csv('./data/penguins_size.csv')

data = data.dropna()
data = data.drop(['sex','island','flipper_length_mm','body_mass_g'], axis=1)

次に、入力データを分離してスケーリングします。

X = data.drop(['species'], axis=1)

ss =StandardScaler()
X = ss.fit_transform(X)

y = data['species']
spicies ={'Adelie':0,'Chinstrap':1,'Gentoo':2}
y =[spicies[item]for item in y]
y = np.array(y)

最後に、データはトレーニングデータセットとテストデータセットに分けられます。

X_train, X_test, y_train, y_test =train_test_split(X, y, test_size=0.2, random_state=33)

データをプロットすると、次のようになります。

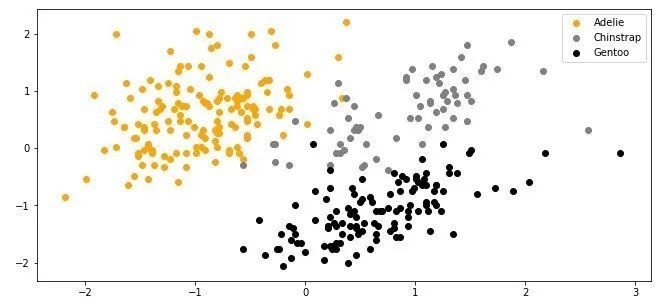
グリッド検索

手動のハイパーパラメータ調整は遅く、煩わしいものです。これが、最初で最も単純なハイパーパラメータ最適化手法であるグリッド検索を検討した理由です。このテクノロジーはプロセスを加速させており、最も一般的に使用されているハイパーパラメーター最適化手法の1つです。基本的に、試行錯誤のプロセスを自動化します。この手法では、すべてのハイパーパラメータ値のリストが提供され、アルゴリズムは可能な組み合わせごとにモデルを構築して評価し、最良の結果を提供する値を選択します。これは、どのモデルにも適用できる一般的な手法です。

この例では、SVMアルゴリズムが分類に使用されています。 3つのハイパーパラメータC、ガンマ、カーネルが考慮されます。それらの詳細については、この記事をご覧ください。 Cの場合は、0.1、1、100、1000の値を確認します。ガンマの場合は、0.0001、0.001、0.005、0.1、1、3、5の値を使用します。カーネルの場合は、「linear」および「rbf」の値を使用します。コードでは次のようになります。

hyperparameters ={'C':[0.1,1,100,1000],'gamma':[0.0001,0.001,0.005,0.1,1,3,5],'kernel':('linear','rbf')}

Sci-Kit LearnとそのSVCクラスを使用します。これには、分類用のSVM実装が含まれています。さらに、グリッド検索の最適化に使用されるGridSearchCVクラスを使用します。組み合わせは次のようになります。

grid =GridSearchCV(
  estimator=SVC(),
  param_grid=hyperparameters,
  cv=5,
scoring='f1_micro',
n_jobs=-1)

このクラスは、コンストラクターを介していくつかのパラメーターを受け取ります。

Estimator-インスタンスのマシン学習アルゴリズム自体。 SVCクラスの新しいインスタンスがそこに渡されます。
param_grid-ハイパーパラメータの辞書が含まれています。
cv-相互検証分割戦略を決定します。
スコアリング-予測を評価するために使用される検証指標。 F1スコアを使用します。
n_jobs-並行して実行するジョブの数を示します。値-1は、すべてのプロセッサが使用中であることを意味します。

あとは、fitメソッドを使用してトレーニングプロセスを実行するだけです。

grid.fit(X_train, y_train)

トレーニング後、最適なハイパーパラメータとこれらのパラメータのスコアを確認できます。

print(f'Best parameters: {grid.best_params_}')print(f'Best score: {grid.best_score_}')
Best parameters:{'C':1000,'gamma':0.1,'kernel':'rbf'}
Best score:0.9626834381551361

同様に、すべての結果を印刷できます。

print(f'All results: {grid.cv_results_}')

Allresults: {'mean_fit_time': array([0.00780015, 0.00280147, 0.00120015, 0.00219998, 0.0240006 ,*

  0.00739942, 0.00059962, 0.00600033, 0.0009994 , 0.00279789,*

  0.00099969, 0.00340114, 0.00059986, 0.00299864, 0.000597  ,*

  0.00340023, 0.00119658, 0.00280094, 0.00060058, 0.00179944,*

  0.00099964, 0.00079966, 0.00099916, 0.00100031, 0.00079999,*

  0.002     , 0.00080023, 0.00220037, 0.00119958, 0.00160012,*

  0.02939963, 0.00099955, 0.00119963, 0.00139995, 0.00100069,*

  0.00100017, 0.00140052, 0.00119977, 0.00099974, 0.00180006,*

  0.00100312, 0.00199976, 0.00220003, 0.00320096, 0.00240035,*

  0.001999  , 0.00319982, 0.00199995, 0.00299931, 0.00199928,   *

...

では、このモデルを作成して、テストデータセットでどのように機能するかを確認してください。

model =SVC(C=500, gamma =0.1, kernel ='rbf')
model.fit(X_train, y_train)

preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9701492537313433

かっこいい、提案されたハイパーパラメータを使用したモデルの精度は約97％です。モデルが描画されたときの外観は次のとおりです。

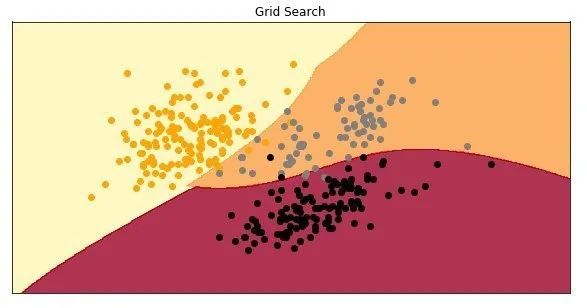
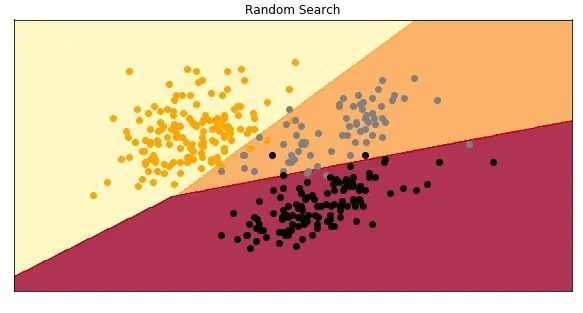
ランダム検索

グリッド検索は非常に簡単です。しかし、それは計算コストもかかります。特に深層学習の分野では、トレーニングに時間がかかる場合があります。同様に、一部のハイパーパラメータは他のハイパーパラメータよりも重要な場合があります。これが、この記事の紹介でランダム検索のアイデアが生まれた理由です。実際、この研究は、計算コストの観点から、ハイパーパラメータの最適化にはグリッド検索よりもランダム検索の方が効果的であることを示しています。この手法により、重要なハイパーパラメータの適切な値をより正確に見つけることもできます。

グリッド検索と同様に、ランダム検索はハイパーパラメータ値のグリッドを作成し、ランダムな組み合わせを選択してモデルをトレーニングします。この方法では最適な組み合わせを見逃す可能性がありますが、グリッド検索と比較すると、予期せず最適な結果がより頻繁に選択され、時間もほとんどかかりません。コードでどのように機能するかを確認してください。 Same = Sci-Kit LearnのSVCクラスを使用しますが、今回はランダム検索の最適化にRandomSearchCVクラスを使用します。

hyperparameters ={"C": stats.uniform(500,1500),"gamma": stats.uniform(0,1),'kernel':('linear','rbf')}

random =RandomizedSearchCV(
    estimator =SVC(),
    param_distributions = hyperparameters,
    n_iter =100,
    cv =3,
    random_state=42,
    n_jobs =-1)

random.fit(X_train, y_train)

Cとガンマには均一な分布が使用されていることに注意してください。結果は印刷することもできます：

print(f'Best parameters: {random.best_params_}')print(f'Best score: {random.best_score_}')

Best parameters: {'C': 510.5994578295761, 'gamma': 0.023062425041415757, 'kernel': 'linear'}*
Best score: 0.9700374531835205*

近いですが、グリッド検索を使用した場合とは結果が異なることに注意してください。グリッド検索のハイパーパラメーターCの値は500であり、ランダム検索のハイパーパラメーターCの値は510.59です。このアイテムだけでは、この値をグリッド検索リストに入れる可能性が低いため、ランダム検索の利点を確認できます。同様に、ガンマの場合、ランダム検索では0.23が得られ、グリッド検索では0.1が得られます。本当に驚くべきことは、ランダム検索がRBFの代わりに線形カーネルを選択し、より高いF1スコアを達成したことです。すべての結果を出力するには、cv_results_属性を使用します。

print(f'All results: {random.cv_results_}')

Allresults: {'mean_fit_time': array([0.00200065, 0.00233404, 0.00100454, 0.00233777, 0.00100009,*

  0.00033339, 0.00099715, 0.00132942, 0.00099921, 0.00066725,*

  0.00266568, 0.00233348, 0.00233301, 0.0006667 , 0.00233285,*

  0.00100001, 0.00099993, 0.00033331, 0.00166742, 0.00233364,*

  0.00199914, 0.00433286, 0.00399915, 0.00200049, 0.01033338,*

  0.00100342, 0.0029997 , 0.00166655, 0.00166726, 0.00133403,*

  0.00233293, 0.00133729, 0.00100009, 0.00066662, 0.00066646,*

....*

グリッド検索と同じことを行います。提案されたハイパーパラメータを使用してモデルを作成し、テストデータセットのスコアを確認して、モデルを描画します。

model =SVC(C=510.5994578295761, gamma =0.023062425041415757, kernel ='linear')
model.fit(X_train, y_train)

preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9701492537313433

テストデータセットのF1スコアは、グリッド検索を使用した場合のスコアとまったく同じです。モデルを表示します。

ベイジアン最適化

最初の2つのアルゴリズムに関する非常にクールな事実は、異なるハイパーパラメーター値を使用したすべての実験を並行して実行できることです。これにより、時間を大幅に節約できます。しかし、これは彼らの最大の欠点でもあります。これは、各実験が独立して行われるため、過去の実験からの情報を現在の実験で使用できないことを意味します。フィールド全体が、シーケンス最適化の問題の解決に専念しています-シーケンスモデルベースの最適化（SMBO）。この分野で探求されたアルゴリズムは、損失関数の以前の実験と観察を使用します。それらに基づいて、次善のポイントを決定してみてください。ベイジアン最適化は、そのようなアルゴリズムの1つです。

SMBOグループの他のアルゴリズムと同様に、以前に評価されたポイント（この場合、これらはハイパーパラメーター値ですが、一般化できます）を使用して、損失関数の事後予測を計算します。このアルゴリズムは、ガウスプロセスと取得関数という2つの重要な数学的概念を使用しています。ガウス分布はランダム変数で行われるため、ガウスプロセスは関数の一般化です。ガウス分布に平均と共分散があるように、ガウスプロセスは平均関数と共分散関数によって記述されます。

取得関数は、現在の損失値を評価するために使用される関数です。それを観察する1つの方法は、損失関数として使用することです。これは、損失関数の事後分布の関数であり、ハイパーパラメーターのすべての値の有用性を説明します。最も人気のある収集機能は改善されると期待されています：

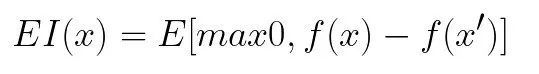
ここで、fは損失関数、x 'は現在の最良のハイパーパラメーターセットです。これらすべてをまとめると、Byesianの最適化は次の3つのステップで実行されます。

以前に評価された損失関数ポイントを使用して、ガウスプロセスを使用して事後予測を計算します。
期待される改善効果を最大化する新しいポイントセットが選択されます
新しく選択したポイントの損失関数を計算します

これをコードに導入する簡単な方法は、通常skoptと呼ばれるSci-Kit最適化ライブラリを使用することです。前の例で使用した手順に従って、次の操作を実行できます。

hyperparameters ={"C":Real(1e-6,1e+6, prior='log-uniform'),"gamma":Real(1e-6,1e+1, prior='log-uniform'),"kernel":Categorical(['linear','rbf']),}

bayesian =BayesSearchCV(
    estimator =SVC(),
    search_spaces = hyperparameters,
    n_iter =100,
    cv =5,
    random_state=42,
    n_jobs =-1)

bayesian.fit(X_train, y_train)

同様に、ハイパーパラメータセットに対して辞書が定義されています。 Sci-KitOptimizationライブラリのRealクラスとCategoricalクラスが使用されることに注意してください。次に、GridSearchCVまたはRandomSearchCVを使用するのと同じ方法でBayesSearchCVクラスを使用します。トレーニング後、最良の結果を印刷できます。

print(f'Best parameters: {bayesian.best_params_}')print(f'Best score: {bayesian.best_score_}')

Best parameters:*
OrderedDict([('C', 3932.2516133086), ('gamma', 0.0011646737978730447), ('kernel', 'rbf')])*
Best score: 0.9625468164794008*

この最適化を使用すると、非常に異なる結果が得られました。ランダム検索を使用する場合よりも損失が大きくなります。すべての結果を印刷することもできます。

print(f'All results: {bayesian.cv_results_}')

All results: defaultdict(<class 'list'>, {'split0_test_score': [0.9629629629629629,*
0.9444444444444444, 0.9444444444444444, 0.9444444444444444, 0.9444444444444444,*
0.9444444444444444, 0.9444444444444444, 0.9444444444444444, 0.46296296296296297,*
0.9444444444444444, 0.8703703703703703, 0.9444444444444444, 0.9444444444444444,*
0.9444444444444444, 0.9444444444444444, 0.9444444444444444, 0.9444444444444444,*
.....*

これらのハイパーパラメータを持つモデルは、テストデータセットでどのように機能しますか？

model =SVC(C=3932.2516133086, gamma =0.0011646737978730447, kernel ='rbf')
model.fit(X_train, y_train)
 
preditions = model.predict(X_test)print(f1_score(preditions, y_test, average='micro'))

0.9850746268656716

これはとても興味深いです。検証データセットで得られた結果が悪い場合でも、テストデータセットでより良いスコアが得られます。これはモデルです：

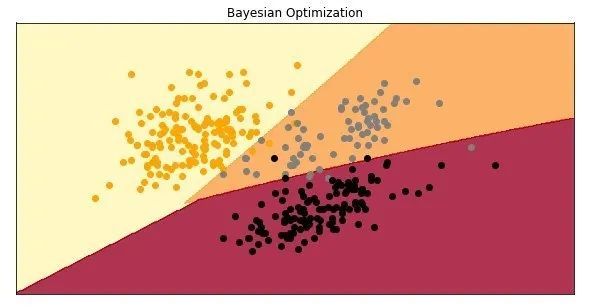
楽しみのために、これらすべてのモデルをまとめてください。

オプション

通常、前述の方法が最も一般的で一般的に使用されます。ただし、前の解決策が適切でない場合は、いくつかの代替方法を検討できます。それらの1つは、ハイパーパラメーター値の勾配ベースの最適化です。この手法では、関連するハイパーパラメータの勾配を計算し、勾配降下アルゴリズムを使用して最適化します。このアプローチの問題は、勾配降下が適切に機能するために、凸状で滑らかな関数が必要になることです。これは、ハイパーパラメーターについて話す場合には通常は当てはまりません。別の方法は、最適化のために進化的アルゴリズムを使用することです。

結論として

この記事では、いくつかのよく知られたハイパーパラメータの最適化と調整のアルゴリズムを紹介します。グリッド検索、ランダム検索、ベイジアン最適化を使用して、ハイパーパラメーターの最良の値を取得する方法を学びました。また、コードでSci-KitLearnクラスとメソッドを使用する方法も確認しました。