Pythonの二項分布、ポアソン分布

迷子にならないようにクリックしてフォロー

鉛

話す

黒板をノックして、乾物が戦場に到着！ ！ ！データ分析では、二項分布とポアソン分布がよく使われる2つの分布です。本日は、二項分布の基礎を簡単に紹介します。ベルヌーイテスト、n倍ベルヌーイテスト、2点分布です。次に、二項分布とポアソン分布の概念を説明します。その後、二項分布をポアソン分布に変換するための条件を説明します。最後に、特定の条件下で二項分布をポアソンに変換できる理由をpythonで見てみましょう。緩い分布は概算です。

ベルヌーイテスト

誰もがコインを投げたと思います。コインを投げたときの結果は2つだけですか？それがポジティブでもネガティブでもない場合、実際、このようなテストはベルヌーイテストです。次に、抽象的な要約を作成しましょう。ランダムテストを想定します。 Eの結果は2つだけで、イベントAが表示され、イベントAは表示されません。同時に、イベントAが表示される確率はpであり、表示されない確率はq、0です。 <p<1,q=1-p,这样的一次试验我们把它叫做伯努利试验。将伯努利试验进行n重独立实验，重复做n次，这样的n重独立实验就是n重伯努利试验。

2点分布

Bernoulliテストに対応する分布は2点分布であり、0-1分布とも呼ばれます。つまり、ランダム変数Xの分布は次のようにリストされます。

注：1は発生の確率を表し、0は発生しない確率を表します

二項分布

n倍ベルヌーイ実験では、イベントAの発生数の対応する分布は二項分布です。つまり、ランダム変数Xの分布は次のようにリストされます。

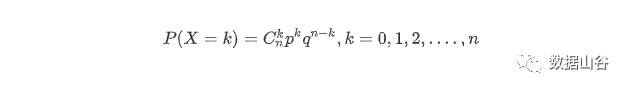
ここで0 <p<1,q=1-p,当n=1时，二项分布就是两点分布。

ポアソン分布

ポアソン分布は、数学者Simeon Denis-Poisson（1781-1840）の名前に由来します。ポアソン分布は、主に連続した時間または空間での離散イベントの数を測定するために使用されます。式は次のとおりです。

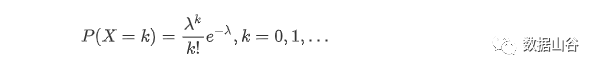
λ> 0は平均発生数を意味します。ランダム変数が二項分布に従う場合、および

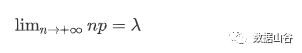
つまり、nが大きく、pが小さい場合、ポアソン分布を使用して二項分布を近似し、問題を解決することができます。なぜでしょうか。

まず、上記のものは実際にはポアソンの定理と呼ばれる正式な名前を持っています。これは定理なので、上記のものを確立する必要があることを意味します。次に、わかりやすい例を見てみましょう。これが理由です。

例として、1日に病院で何人の赤ちゃんが生まれるのかという質問をしてみましょう（この質問はポアソンの分布に従います）。

思考の限界でこの日の時間を取り、それをn個の小さな期間に無限に細分化することができます。それぞれの小さな期間で、赤ちゃんが生まれる、赤ちゃんが生まれないという2つの結果しかありません。これはそうですか？短い期間はランダムな実験と見なすことができ、テストの結果は2回の出生のみで、出生なしであるため、分布を使用して、n回の短い期間をn回のベルヌーイテストと見なすことができるかどうか説明：それは二項分布です。ポアソン分布は二項分布に変換されますか？つまり、簡単に言えば、nが大きく、pが小さい場合、二項分布はポアソン分布、ポアソン分布は二項分布です。もちろん、代わりに概算することもできます。

次に、コンピューターを使用してこの結果をシミュレートします。

**注：一般に、n> = 20およびp <= 0.05の場合、ポアソン分布を使用して二項分布を概算できます。 ****

01

pythonの実装

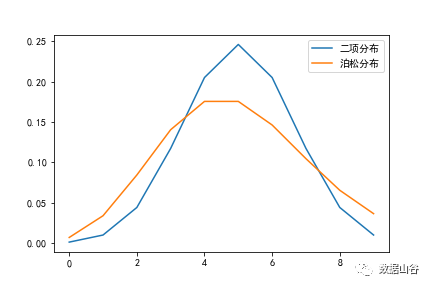
nが10でp = 0.5の場合、上記の条件により、二項分布はポアソン分布で近似されるべきではないことがわかります。下の図は、nが10でp = 0.5の場合、二項分布とポアソン分布も明らかに異なります（特定のコードについては以下を参照してください）

# 対応するライブラリをインポートします
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# 二項分布とポアソン分布をプロットする
n =10
p=0.5
q=1-p
bino = stats.binom(n,p)
x = np.arange(0,n)
y1 = bino.pmf(x)
possion = stats.poisson(n*p)
y2 = possion.pmf(x)
plt.plot(x,y1,label="二項分布")
plt.plot(x,y2,label="ポアソン分布")
plt.legend()
plt.show()

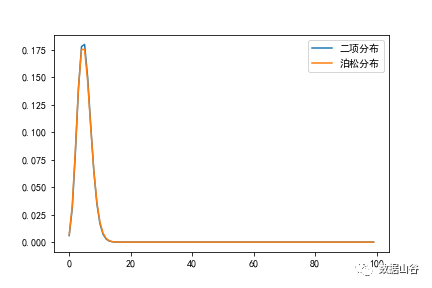
nが100、p = 0.05の場合、上記の条件により、二項分布はほぼポアソン分布に置き換えられることがわかります。下図は、nが100、p = 0.05の場合、二項分布とポアソン分布が非常に似ています（特定のコードについては以下を参照してください）

# 対応するライブラリをインポートします
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# 二項分布図とポアソン分布図を描く
n =100
p=0.05
q=1-p
bino = stats.binom(n,p)
x = np.arange(0,n)
y1 = bino.pmf(x)
possion = stats.poisson(n*p)
y2 = possion.pmf(x)
plt.plot(x,y1,label="二項分布")
plt.plot(x,y2,label="ポアソン分布")
plt.legend()
plt.show()

02

総括する

今日は主に、いわゆる二項分布、ポアソン分布、および二項分布のポアソン分布のおおよその置き換えについて学びました。誰もがこの2つの関係をすでに理解しているはずです。次のセクションでは、二項分布と通常分布に焦点を当て、それらの間にどのような「愛と憎しみ」があるかを明らかにしますので、ご期待ください！