Python Romberg method to find integral examples

I will stop talking nonsense, just go to the code!

# Romberg method to find integral
import math
a=0    #Points lower limit
b=1    #Point upper limit
eps=10**-5  #Precision
T=[]   #Complex ladder sequence
S=[]   #Simpson sequence
C=[]   #Cotes sequence
R=[]   #Romberg sequence
def func(x): #Integrand
 y=math.exp(-x)return y
def Romberg(a,b,eps,func):
 h = b - a
 T.append(h *(func(a)+func(b))/2)
 ep=eps+1
 m=0while(ep =eps):
 m=m+1
 t=0for i inrange(2**(m-1)-1):
 t=t+func(a+(2*(i+1)-1)*h/2**m)*h/2**m
 t=t+T[-1]/2
 T.append(t)if m =1:
 S.append((4**m*T[-1]-T[-2])/(4**m-1))if m =2:
 C.append((4**m*S[-1]-S[-2])/(4**m-1))if m =3:
 R.append((4**m*C[-1]-C[-2])/(4**m-1))if m 4:
 ep=abs(10*(R[-1]-R[-2]))Romberg(a,b,eps,func)
# print(T)
# print(S)
# print(C)
# print(R)
# Computer reference value 0.6321205588print("The integration result is:{:.5f}".format(R[-1]))

Supplementary extension: Romberg quadrature formula for numerical analysis in python

The compound trapezoidal formula is put forward:

1. First, what is the trapezoidal formula:

The trapezoidal formula shows: the integral (area) of f(x) between the two points [a,b] can be approximately expressed by the area of a trapezoid.

2. Obviously, this trapezoidal formula has different algebraic precision for different f(x). In order to be able to fit more f(x), we generally use the Newton-Cotes formula which is a higher order formula to perform numerical integration. But the disadvantage of higher order is that when the order is greater than 8, the quadrature formula will be unstable. Therefore, the Newton-Cortez formulas we use for numerical integration are usually the first-order trapezoidal formula, the quadratic Simpson formula, and the 4-order Cortez formula.

Simpson formula:

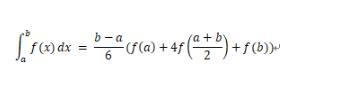
Cortez formula:

3. The Newton-Cortez formula cannot be used if the order is higher than 8 times, but the low order formula is not accurate enough. The solution is to use: compound trapezoidal quadrature formula. The compound quadrature formula is to divide n cells between cells on the interval [a, b]. Using the trapezoidal formula once on a large interval [a,b] is not accurate enough, then use the trapezoidal formula between n cells, and finally add up the sum of the cells to get the integral approximation of the entire large interval [a,b] .

a = x0 < x1 <x2 …<xn-1 < xn =b

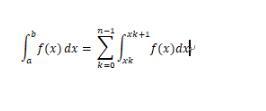
Let Tn be the complex trapezoidal quadrature formula that divides [a, b] into n equal parts, and h = (ba)/n is the length between cells. h/2 is similar to (ba)/2 in the trapezoidal formula

Note: k+1 here is a subscript

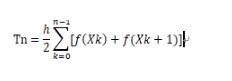
Through research, we found that there is some recurrence relationship between T2n and Tn.

Note: k+1/2 here is a subscript. And where h/2 is in h is Tn (h in n equal division = (ba)/n))

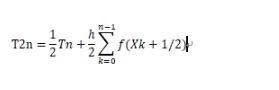
Ever since, we can launch T1, T2, T4, T8...T2n sequences at once

After introducing these, it is our topic: Romberg's quadrature formula

The essence of Romberg's quadrature formula is to construct with T2n sequence, S2n sequence,

Then use the S2n sequence to construct the C2n sequence

Finally, the C2n sequence is used to construct the R2n sequence.

To realize it by programming, just understand the following formulas.

The python programming code is as follows:

# coding=UTF-8
# Author:winyn
'''
Given a function, such as: f(x)= x^(3/2), and the upper and lower limit of integral a,b. Use the mechanical quadrature Romberg formula to find the integral.

'''
import numpy as np

def func(x):return x**(3/2)classRomberg:
 def __init__(self, integ_dowlimit, integ_uplimit):'''
 Initialize integral upper limit integ_uplimit and lower limit integ_dowlimit
 Input a function, output the integral of the function at the upper and lower limits of the integral

  '''
 self.integ_uplimit = integ_uplimit
 self.integ_dowlimit = integ_dowlimit

 def calc(self):'''
 Calculate the four sequences of Richardson's extrapolation algorithm

  '''
 t_seq1 = np.zeros(5,'f')
 s_seq2 = np.zeros(4,'f')
 c_seq3 = np.zeros(3,'f')
 r_seq4 = np.zeros(2,'f')
 # Cycle generation of hm spacing sequence
 hm =[(self.integ_uplimit - self.integ_dowlimit)/(2** i)for i inrange(0,5)]print(hm)
 # Cycle generation t_seq1
 fa =func(self.integ_dowlimit)
 fb =func(self.integ_uplimit)

 t0 =(1/2)*(self.integ_uplimit - self.integ_dowlimit)*(fa+fb)
 t_seq1[0]= t0

 for i inrange(1,5):
 sum =0
 # The cumulative sum of the extra points
 for each inrange(1,2**i,2):
 sum =sum + hm[i]*func( self.integ_dowlimit+each * hm[i])#Calculate two values
 temp1 =1/2* t_seq1[i -1]
 temp2 =sum
 temp = temp1 + temp2
 # Find t_seql 1-4 bit
 t_seq1[i]= temp
 print('T sequence:'+str(list(t_seq1)))
 # Loop generation s_seq2
 s_seq2 =[round((4* t_seq1[i +1]- t_seq1[i])/3,6)for i inrange(0,4)]print('S sequence:'+str(list(s_seq2)))
 # Loop generation c_seq3
 c_seq3 =[round((4**2* s_seq2[i +1]- s_seq2[i])/(4**2-1),6)for i inrange(0,3)]print('C sequence:'+str(list(c_seq3)))
 # Cycle generation r_seq4
 r_seq4 =[round((4**3* c_seq3[i +1]- c_seq3[i])/(4**3-1),6)for i inrange(0,2)]print('R sequence:'+str(list(r_seq4)))return'end'

rom =Romberg(0,1)print(rom.calc())

The above example of Python Romberg's method for calculating integrals is all the content shared by the editor. I hope to give you a reference.