pythonに基づいて凸型船体の問題を解決します

最近、パイソンアルゴリズムの本を読んでいました。1年前に本を購入しました。休憩中に充電することを学びました。ついにこの本を見ましたが、少し難しいです。当時のコメントはあまり理解できなかったのですが、最後に、そこに書かれているアルゴリズムの問題という方法を考えて、Baidupythonを使って解決しました。これはかなりいいと思います。

**以下は、凸型船体問題のコードです。 ****

# - *- coding: utf-8-*-import turtle
import random
import time
f=open('point.txt','w')for i inrange(100):
 x=random.randrange(-250,250,10)
 y=random.randrange(-200,200,10)
 f.write(str(x)+','+str(y)+'\n')
f.close()
point=[]
 
f=open('point.txt')for i in f:try:
 temp=i.split(',')
 x=float(temp[0]); y=float(temp[1])
 point.append((x,y))
 except :
 print 'a err'
f.close()
 
point=list(set(point))#重複するポイントを削除する
 
n=0for i inrange(len(point)):if point[n][1] point[i][1]:
 n=i
 
p0=point[n]
point.pop(n)
def compare(a,b):
 x=[a[0]-p0[0],a[1]-p0[1]]
 y=[b[0]-p0[0],b[1]-p0[1]]
 dx=(x[0]**2+x[1]**2)**0.5
 dy=(y[0]**2+y[1]**2)**0.5
 cosa=x[0]/dx
 cosb=y[0]/dy
 if cosa < cosb:return1
 elif cosa   cosb:return-1else:if dx<dy:return-1
 elif dx dy:return1else:return0
 
point.sort(compare)
point.insert(0,p0)
ep=point[:]#要素をコピーし、操作epはポイントに影響しません
tag=0while tag==0:
 tag=1
 l=len(ep)for i inrange(l):
 i1,i2,i3=(i,(i+1)%l,(i+2)%l)
 x,y,z=(ep[i1],ep[i2],ep[i3])
 a1,a2=((y[0]-x[0],y[1]-x[1]),(z[0]-y[0],z[1]-y[1]))if a1[0]*a2[1]-a1[1]*a2[0]<0:
 tag=0
 ep.pop(i2)break
 elif a1[0]*a2[1]-a1[1]*a2[0]==0 and a1[0]*a2[0]<0:
 #==0 書き直す必要があります,360度の状況
 tag=0
 ep.pop(i2)break
 
 
def drawpoint(point,color,line):
 p=turtle.getturtle()
 p.hideturtle()
 turtle.delay(1)if(line=='p'):
 p.speed(0)for i in point:
 p.pu()
 p.color(color)
 p.goto(i)
 p.pd()
 p.dot()elif(line=='l'):
 p.pu()
 p.speed(1)for i in point:
 p.color(color)
 p.goto(i)
 p.pd()
 p.dot()
 p.goto(point[0])drawpoint(point,'black','p')drawpoint(ep,'red','l')
time.sleep(1)

補足知識：ブルートフォースアルゴリズムと凸型船体問題のpython実装

ブルートフォース法の基本的な考え方は、最初に除去法を使用して凸型船体の頂点を決定し、次にこれらの頂点を反時計回りの順序で出力することです。点Pが凸型船体の頂点であるかどうかを判断する場合、次の特性があります。

平面点セットS、P、Pi、Pj、PkがSの4つの異なる点であるとすると、PがPi、Pj、Pkによって形成される三角形の内側または境界上にある場合、PはSの凸型船体頂点ではありません。

では、点Pが三角形の内側または境界上にあるかどうかをどのように判断するのでしょうか。平面上の2つの点ABが与えられ、線形方程式g（A、B、P）= 0の場合、Pは直線上にあり、g（A、B、P）0およびg（A、B、P）<0、Pの場合はそれぞれ直線の両側にあります。

点Pが三角形の内側または境界上にあることを確認するには、Pと三角形の各頂点が、三角形の他の2つの頂点によって決定される線の同じ側にあるかどうかを確認するだけです。

t1=g(pj,pk,p)*g(pj,pk,pi) =0 ,
t2=g(pi,pk,p)*g(pi,pk,pj) =0,
t3=g(pj,pi,p)*g(pj,pi,pk) =0

両方とも確立されています

凸型船体問題のブルートフォースアルゴリズムの疑似コードは次のとおりです。

BruteForce(S)：

入力：平面上のn点のセットS

出力：Sの凸型船体のすべての頂点を反時計回りに出力します

n = 3の場合、Sの頂点を反時計回りに出力すると、アルゴリズムは終了して、Sの縦座標が最小の点Pを見つけます。

For S Doの任意の3つのポイントPi、Pj、Pk Pi、Pj、Pkの場合1つのポイントは、他の2つのポイントとPによって形成される三角形にあります。次に、ポイントを削除します。

Sで、横軸が最小の点Aと横軸が最小の点Bを見つけます。

Sを線ABの上の点セットSUと線ABの下の点セットSLに分割します。2つの点AとBはSLに属します。

SLを横軸の昇順で並べ替え、SL、SUを横軸の降順で出力します。

最初にランダムにポイントセットSを生成します

import random
import itertools

def generate_num(n):
 random_list =list(itertools.product(range(1,100),range(1,100)))
 lists=random.sample(random_list, n)return lists

点Pが三角形の内側にあるか境界上にあるか、つまり点Pが凸状の船体にあるかどうかを判別します。

特定の判断プロセスでは、特に座標点が密集している場合、さらに3つの特殊なケースがあります。

直線を形成する2点はx軸に垂直です

点Pを除く他の3点が直線上にある場合、点Pはこの時点で凸型船体上の点である可能性があるため、削除しないでください。

点Pを除く他の3点が直線上にあり、x軸に垂直である場合、点Pはこの時点で凸型船体上の点である可能性があるため、削除しないでください。

# piがpjにあるかどうかを確認します,pk,p0は三角形を形成し、t1を返します,t2,t33つの変数
def isin(pi,pj,pk,p0):
 x1 =float(p0[0])
 x2 =float(pj[0])
 x3 =float(pi[0])
 x4 =float(pk[0])
 y1 =float(p0[1])
 y2 =float(pj[1])
 y3 =float(pi[1])
 y4 =float(pk[1])

 k_j0=0
 b_j0=0
 k_k0=0
 b_k0=0
 k_jk=0
 b_jk=0
 perpendicular1=False
 perpendicular2 = False
 perpendicular3 = False
 # pj,p0で構成される直線、piを見てください,pkがラインの同じ側にあるかどうか

 if x2 - x1 ==0:
 # pj,p0がX軸に垂直な直線を構成する場合
 t1=(x3-x2)*(x4-x2)
 perpendicular1=True
 else:
 k_j0 =(y2 - y1)/(x2 - x1)
 b_j0 = y1 - k_j0 * x1
 t1 =(k_j0 * x3 - y3 + b_j0)*(k_j0 * x4 - y4 + b_j0)

 # pk,p0で構成される直線、piを見てください,pjが線の同じ側にあるかどうか

 if x4 - x1 ==0:
 # pk,p0がX軸に垂直な直線を構成する場合
 t2=(x3-x1)*(x2-x1)
 perpendicular2=True
 else:
 k_k0 =(y4 - y1)/(x4 - x1)
 b_k0 = y1 - k_k0 * x1
 t2 =(k_k0 * x3 - y3 + b_k0)*(k_k0 * x2 - y2 + b_k0)

 # pj,pkで構成される行、piを見てください,p0が線の同じ側にあるかどうか

 if x4 - x2 ==0:
 # pj,pkがX軸に垂直な直線を構成する場合
 t3=(x3-x2)*(x1-x2)
 perpendicular3 = True
 else:
 k_jk =(y4 - y2)/(x4 - x2)
 b_jk = y2 - k_jk * x2
 t3 =(k_jk * x3 - y3 + b_jk)*(k_jk * x1 - y1 + b_jk)
 # pkの場合、p0,pj、3点が同じ直線上にある場合、その点は削除できません
 if(k_j0 * x4 - y4 + b_j0)==0and(k_k0 * x2 - y2 + b_k0)==0and(k_jk * x1 - y1 + b_jk)==0:
 t1=-1
 # pkの場合、p0,pj、3つのポイントが同じ直線上にあり、X軸に垂直である場合、そのポイントは削除できません。
 if perpendicular1 and perpendicular2 and perpendicular3:
 t1=-1return t1,t2,t3

次は、凸型船体上の点を見つけるために使用される実装アルゴリズムの主要部分です

import isintriangle

def force(lis,n):
 # セットSのポイント数が3の場合、セット自体が凸型船体セットになります。
 if n==3:return lis
 else:
 # コレクションは縦座標でソートされ、yが最小の点p0を見つけます
 lis.sort(key=lambda x: x[1])
 p0=lis[0]
 # p0の残りのポイントセットlisを削除します_brute
 lis_brute=lis[1:]
 # tempは、lisのコレクションで削除する必要のあるポイントを格納するために使用されます_野蛮なインデックス。4つのポイントの1つが、他の3つのポイントによって形成される三角形の内側にある場合、そのポイントは凸型の船体上のポイントであってはなりません。
 temp=[]
 # トリプルループは、三角形内のそのようなすべてのポイントを見つけます
 for i inrange(len(lis_brute)-2):
 pi=lis_brute[i]
 # インデックスiがすでに一時的である場合、つまりpiが凸型船体上の点であってはならない場合は、このループをスキップしてください
 if i in temp:continuefor j inrange(i+1,len(lis_brute)-1):
 pj=lis_brute[j]
 # インデックスjがすでに一時的である場合、つまりpjが凸型船体上の点であってはならない場合は、このループをスキップしてください
 if j in temp:continuefor k inrange(j +1,len(lis_brute)):
  pk=lis_brute[k]

  # インデックスkがすでに一時的である場合、つまりpkが凸型船体上の点であってはならない場合は、このループをスキップしてください
  if k in temp:continue
  # piがpjにあるかどうかを判別します,pk,p0によって形成される三角形の内側(it1,it2,it3)=isintriangle.isin(pi,pj,pk,p0)if it1 =0 and it2 =0 and it3 =0:if i not in temp:
  temp.append(i) 
  # pjがpiにあるかどうかを判別する,pk,p0によって形成される三角形の内側(jt1,jt2,jt3)=isintriangle.isin(pj,pi,pk,p0)if jt1 =0 and jt2 =0 and jt3 =0:if j not in temp:
  temp.append(j)

  # pkがpjにあるかどうかを確認します,pi,p0によって形成される三角形の内側(kt1, kt2, kt3)= isintriangle.isin(pk, pi, pj, p0)if kt1  =0 and kt2  =0 and kt3  =0:if k not in temp:
  temp.append(k)
 # listlastは、最終的に選択された凸型ハルセットです。
 lislast=[]for coor in lis_brute:
 loc =[i for i, x inenumerate(lis_brute)if x == coor]for x in loc:
 ploc = x
 if ploc not in temp:
 lislast.append(coor)
 # 凸型船体セットにp0を追加します
 lislast.append(p0)return lislast

最後に、凸型ハルセットの出力は言うまでもありませんが、疑似コードに従って実装できます。凸型ハルブルートフォースアルゴリズムの結果、ポイントセットのサイズは1000になります。

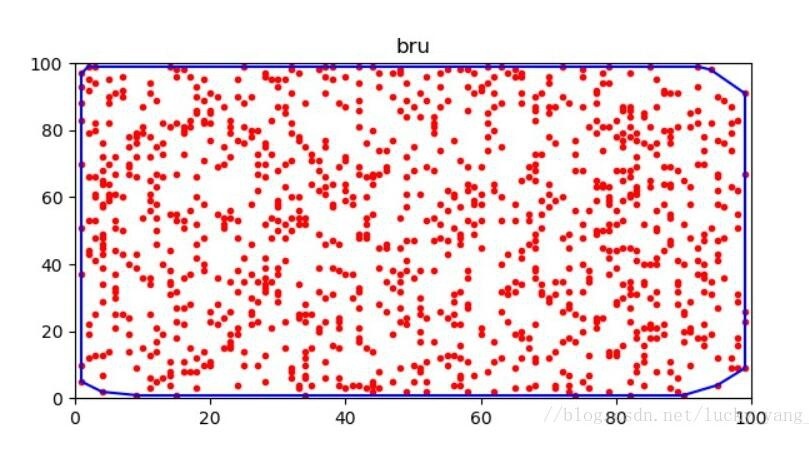
python凸型船体問題に基づく上記の解決策は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。