不可欠な例を見つけるためのPythonRombergメソッド

私はナンセンスな話をやめます、ただコードに行ってください！

# 積分を見つけるためのロンバーグ法
import math
a=0    #ポイント下限
b=1    #クレジット制限
eps=10**-5  #精度
T=[]   #複雑なラダーシーケンス
S=[]   #シンプソンシーケンス
C=[]   #コートシーケンス
R=[]   #ロンバーグシーケンス
def func(x): #インテグランド
 y=math.exp(-x)return y
def Romberg(a,b,eps,func):
 h = b - a
 T.append(h *(func(a)+func(b))/2)
 ep=eps+1
 m=0while(ep =eps):
 m=m+1
 t=0for i inrange(2**(m-1)-1):
 t=t+func(a+(2*(i+1)-1)*h/2**m)*h/2**m
 t=t+T[-1]/2
 T.append(t)if m =1:
 S.append((4**m*T[-1]-T[-2])/(4**m-1))if m =2:
 C.append((4**m*S[-1]-S[-2])/(4**m-1))if m =3:
 R.append((4**m*C[-1]-C[-2])/(4**m-1))if m 4:
 ep=abs(10*(R[-1]-R[-2]))Romberg(a,b,eps,func)
# print(T)
# print(S)
# print(C)
# print(R)
# コンピュータ参照値0.6321205588print("統合の結果は次のとおりです。{:.5f}".format(R[-1]))

補足拡張：pythonでの数値分析のためのRomberg直交式

複合台形式が提案されています：

まず、台形の式は何ですか：

台形の公式は次のことを示しています：2つの点[a、b]間のf（x）の積分（面積）は、台形の面積でおおよそ表すことができます。

明らかに、この台形の公式は、f（x）ごとに代数的精度が異なります。より多くのf（x）に適合できるようにするために、通常、数値積分を実行するための高次式であるNewton-Cotes式を使用します。ただし、高次の欠点は、次数が8より大きい場合、直交式が不安定になることです。したがって、数値積分に使用するニュートン-コルテス式は、通常、1次台形式、2次シンプソン式、および4次コルテス式です。

シンプソンの公式：

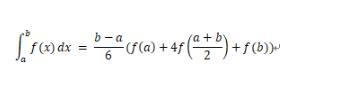
コルテスの公式：

Newton-Cortezの式は、8倍を超える次数では使用できませんが、低次の式は十分に正確ではありません。解決策は次のとおりです。複合台形直交式。複合直交式は、間隔[a、b]でn個のセルをセル間で分割することです。大きな間隔で一度台形式を使用する[a、b]は十分に正確ではありません。次に、n個のセル間で台形式を使用し、最後にセルの合計を合計して、大きな間隔全体の整数近似を取得します[a、b] 。

a = x0 < x1 <x2 …<xn-1 < xn =b

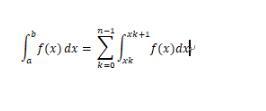
Tnを[a、b]をn個の等しい部分に分割する複雑な台形直交式とし、h =（ba）/ nはセル間の長さです。 h / 2は台形式の（ba）/ 2に似ています

注：ここでのk +1は添え字です

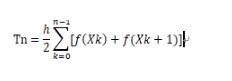
調査の結果、T2nとTnの間には再発関係があることがわかりました。

注：ここでのk +1/2は添え字です。そして、h / 2がhにある場合、Tn（nに等しい除算=（ba）/ n））

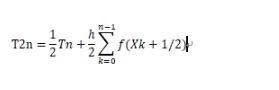
それ以来、T1、T2、T4、T8 ... T2nシーケンスを一度に起動できます

これらを紹介した後、それは私たちのトピックです：ロンバーグの直交式

Rombergの直交式の本質は、T2nシーケンス、S2nシーケンス、

次に、S2nシーケンスを使用してC2nシーケンスを構築します

最後に、C2nシーケンスを使用してR2nシーケンスを構築します。

プログラミングで実現するには、次の式を理解してください。

pythonプログラミングコードは次のとおりです。

# coding=UTF-8
# Author:winyn
'''
次のような関数が与えられます：f(x)= x^(3/2）、および積分の上限と下限a,b。機械的直交ロンバーグ式を使用して積分を見つけます。

'''
import numpy as np

def func(x):return x**(3/2)classRomberg:
 def __init__(self, integ_dowlimit, integ_uplimit):'''
 積分上限整数を初期化する_上限と下限の整数_dowlimit
 関数を入力し、積分の上限と下限で関数の積分を出力します

  '''
 self.integ_uplimit = integ_uplimit
 self.integ_dowlimit = integ_dowlimit

 def calc(self):'''
 リチャードソンの外挿アルゴリズムの4つのシーケンスを計算します

  '''
 t_seq1 = np.zeros(5,'f')
 s_seq2 = np.zeros(4,'f')
 c_seq3 = np.zeros(3,'f')
 r_seq4 = np.zeros(2,'f')
 # hm間隔シーケンスのサイクル生成
 hm =[(self.integ_uplimit - self.integ_dowlimit)/(2** i)for i inrange(0,5)]print(hm)
 # サイクル生成t_seq1
 fa =func(self.integ_dowlimit)
 fb =func(self.integ_uplimit)

 t0 =(1/2)*(self.integ_uplimit - self.integ_dowlimit)*(fa+fb)
 t_seq1[0]= t0

 for i inrange(1,5):
 sum =0
 # 余分なポイントの累積合計
 for each inrange(1,2**i,2):
 sum =sum + hm[i]*func( self.integ_dowlimit+each * hm[i])#2つの値を計算する
 temp1 =1/2* t_seq1[i -1]
 temp2 =sum
 temp = temp1 + temp2
 # tを見つける_seql 1-4ビット
 t_seq1[i]= temp
 print('Tシーケンス：'+str(list(t_seq1)))
 # ループ生成_seq2
 s_seq2 =[round((4* t_seq1[i +1]- t_seq1[i])/3,6)for i inrange(0,4)]print('Sシーケンス：'+str(list(s_seq2)))
 # ループ生成c_seq3
 c_seq3 =[round((4**2* s_seq2[i +1]- s_seq2[i])/(4**2-1),6)for i inrange(0,3)]print('Cシーケンス：'+str(list(c_seq3)))
 # サイクル生成r_seq4
 r_seq4 =[round((4**3* c_seq3[i +1]- c_seq3[i])/(4**3-1),6)for i inrange(0,2)]print('Rシーケンス：'+str(list(r_seq4)))return'end'

rom =Romberg(0,1)print(rom.calc())

上記のPythonRombergの積分計算方法の例は、エディターが共有するすべてのコンテンツです。参考にしてください。