Python（13）入門

Python入門（13/18）
**セクション13 **アプリケーションケース（1）

みなさん、こんにちは！前の段階での集中的な研究の後、私たちはついに奇跡を目撃する瞬間を迎えました。

今日は、6つのアプリケーションケースの設計とプログラミングを通じてpythonがもたらす驚きを体験し、第1段階の学習結果を統合します。

ナインナイン乗算式テーブルをコンパイルします
修飾された整数を見つける
繰り返し番号なしで順列と組み合わせを実現
売上に基づいてボーナスを計算する
python構文のバブルソートメソッドを作成する
データのセットに従って任意の列で並べ替える

6 この場合、3つの数学的な問題と3つのプログラムアルゴリズムの問題があり、Pythonプログラミングのアイデアと方法をよりよく理解するのに役立ちます。このレッスンでは、最初に最初の3つのケースを紹介します。

ケース1.9-9乗算の式テーブルをコンパイルします

要求する：

1、少なくとも、乗算式テーブルが何であるかを知っている必要があります。

2、すべての計算と結果をリストしてください。

3、乗数1〜9によると、ディスプレイは9列に配置されています。

分析：

1、 2つの変数を乗算計算の2つの乗数として定義します：i、値1〜9、j、値1〜9。

2、 2つのトラバーサル：iで1〜9の数値をトラバースし（これはループの最初のレベルです）、各数値が取得されると、それぞれjで1〜9の数値が乗算されます。これは2番目のトラバーサルであり、第1レベルのループ内の第2レベルのループでもあります。したがって、ネストされたループ操作プロセスがあります。

3、式をリストし、9行に配置します。表示形式の問題です。解決策は非常に簡単です。iをトラバースし、式とそれを同じ行のjのすべての数で乗算した結果を配置する必要があります。

PS：複数の計算式と計算結果を同じ行に表示するにはどうすればよいですか？方法は簡単です。すべての計算と計算結果を文字列式で表すことができますよね？次に、1回の反復のすべての文字列を連結（追加）して、長い文字列を取得しますか？それからそれを見せてください、わかりました！

ナインナイン乗算式テーブルのソースコード

コード分析：

1、最初の行のループステートメントは、1〜9のi値を定義します。forとrangeの概念がわかりません。

2、 y変数を定義します。これは、jのiの値に1〜9を掛けて形成された文字列とその結果を表示するために使用されます。

3、 3行目では、2番目のループステートメントが1〜9のj値を定義しています。

4、 4行目では、formatting（placeholder）メソッドを使用して、独立した式と計算結果の文字列xを定義します。

5、文字列の「追加」を使用して、xをyに連結します。

6、 y文字列を表示します。iのforループにあるコードインデントに注意してください。9行で表示されます。

ケース2.修飾された整数を探す

要求する：

整数iを設定します。i+ 100は完全な二乗数であり、さらに168は完全な二乗数です。iの値を見つけてください。

分析：

1、完全な正方形とは、正方形をルート化でき、結果が整数のままであることを意味します。

2、要件：i + 100は完全な二乗数であり、i + 100 +168も完全な二乗数です。

解決策を探しています：

1、 i + 100は完全な二乗数であるため、その二乗根の結果は整数xと見なされます。逆に、xの二乗もi + 100に等しくなります。同様に、i + 100 +168の二乗根の結果が整数yの場合、次に、yの2乗もi + 100 +168に等しくなります。

2、直感的には、上記の条件を満たすiの値を推測することはできません。ただし、プログラミングの利点は、より広いデータ範囲で試行錯誤して、修飾されたi値を見つけることができることです。

3、 100,000以内の試行錯誤を検討できます。最初に、i + 100の二乗を取り、整数を取り、それをxに割り当て、次にi + 268を二乗に丸めて、yに割り当てます。次に、xとyの2乗がi +100とi + 268に等しいかどうかを判断します。等しい場合、iの値は正の解です。

修飾された整数のソースコードを見つける

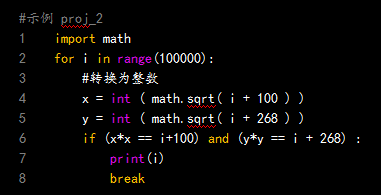
コード分析：

1、最初の行は、数学計算に使用されるimportを介して数学モジュールmathをインポートします（平方根）。

2、 i変数を定義し、0〜100,000の値を取ります。

3、 4行目と5行目の正方形は丸められ、xとyに割り当てられます。

4、 6行目、条件付き判断。

5、条件が満たされると、ループが終了し（試行およびエラー）、現在のi値が出力（表示）されます。

ケース3.繰り返し番号なしで順列と組み合わせを実現

**要件：**互いに異なり、繰り返し番号がない4つの番号（1〜4など）の可能なすべての組み合わせをリストしてください。（ネットワークケースから学ぶ）

分析：

1、まず、4つの数値を列挙する必要があります（例：range（1,5））。

2、それらの順列と組み合わせを計算し、それらを表示可能な変数に割り当てます。

3、重複する番号を削除します。

繰り返し番号なしで順列と組み合わせのソースコードを実現

コード分析：

1、まず、mysetという空のセットを作成します。（コレクションは重量を取り除くのに役立ちます）

2、それぞれ4つのforループを作成し、4つの変数i、j、k、mを定義します。これらは、4桁の1つを表す1〜4の値を取ることができます。

3、コードのインデント、iの値はjのすべての値に対応し、jの値はkのすべての値に対応し、kの値はmのすべての値に対応することに注意してください。

4、各ラウンドのすべての値が取得された後、重複を削除するためにそれらがmysetに追加されます。

5、最後に、すべての反復が完了し、取得された最終的なmysetが目的の結果になります。データのセットの読み取りと表示は、forループ反復メソッドにも適用されます。

概要

このセクションでは、3つのPythonアプリケーションケースを共有しました。それらは数学的なアプリケーションに比較的焦点を当てているようですが、実際には、Pythonの基本的な構文とデータ構造の理解を深めることは有益です。次のレッスンで共有するアプリケーションはあと3つ残っています。

次の3つのアプリケーションでは、データ構造とアルゴリズムの実践を探求し、体験することに焦点を当てます。これは、プログラマーにとってより重要な実践です。