グレーレベルの同時発生マトリックス（Pythonコードを使用）

理論的な内容はhttps://blog.csdn.net/qq_37059483/article/details/78292869から引用されています

最近、機械学習関連のコンテンツを勉強していて、後でブログにまとめていくように頑張っていきますが、友人からSVRサポートベクトル回帰に基づく画質評価方法の実装を手伝ってほしいと頼まれましたが、記事の冒頭で発見しました。
なじみのない男、グレーレベルの共起マトリックスがこの記事を持っています。

メインリファレンスブログ1：[http://blog.csdn.net/jialeheyeshu/article/details/51337225]（http://blog.csdn.net/jialeheyeshu/article/details/51337225）
メインリファレンスブログ2：[http://blog.csdn.net/guanyuqiu/article/details/53117507]（http://blog.csdn.net/guanyuqiu/article/details/53117507）
メインリファレンスブログ3：[http://www.cnblogs.com/rong86/p/3695621.html]（http://www.cnblogs.com/rong86/p/3695621.html）
メインリファレンスブログ4：[http://blog.csdn.net/lingtianyulong/article/details/53032034]（http://blog.csdn.net/lingtianyulong/article/details/53032034）

グレーレベル共起マトリックス生成の原理
グレーレベル共起行列（GLDM）の統計的手法は、1970年代初頭にR. Haralick et al。によって提案されました。画像内のピクセル間の空間分布関係には、画像テクスチャ情報が含まれていることを前提として提案されています。広範なテクスチャ分析方法。

グレーレベル共起行列は、グレーレベルiのピクセルポイントから始まる固定位置（距離d、方位角）を離れるポイントでのグレー値の確率として定義されます。つまり、すべての推定値は次のように表すことができます。マトリックスの形式は、グレーレベルの同時発生マトリックスと呼ばれます。テクスチャの変化が遅い画像の場合、グレーレベルの同時発生マトリックスの対角線上の値は大きくなります。テクスチャの変化が速い画像の場合、グレーレベルの共起マトリックスの対角線上の値は小さくなります。値が大きくなります。グレーレベル共起行列のデータ量が多いため、通常、テクスチャを区別するための機能として直接使用されるのではなく、テクスチャ分類機能として構築されたいくつかの統計に基づいています。ハラリックはかつて、グレーレベルの共起行列に基づいて計算された14種類の統計を提案しました。つまり、エネルギー、エントロピー、コントラスト、均一性、相関、分散、合計平均、合計分散、合計エントロピー、差分散、差平均、差エントロピーです。、関連情報の測定と最大相関係数。

インターネットでグレーレベルの同時発生マトリックス生成の例をたくさん読んでいます。はっきりしているとは思いません。そうでない場合は、結果を直接アップロードするか、理解できないコードや式をたくさん提供します。後でmatlabの概要を読みます。実際、とても簡単です。以下を3回注意深く読んで、それがどのようにして起こったのかを理解してください。（ 3番目の記事を理解しました。当時はとても緊張していました。大丈夫だと思います）
次の図は、グレーレベルの同時発生マトリックスを解決する方法を示しています。（1,1）ポイントを例にとると、GLCM（1,1）の値が1の場合、グレーレベルが1のピクセルのペアのみが水平方向に隣接していることを意味します。 GLCM（1、2）の値は2です。これは、水平方向に1と2のグレースケールを持つ2組のピクセルが隣接しているためです。（MatLabドキュメント）

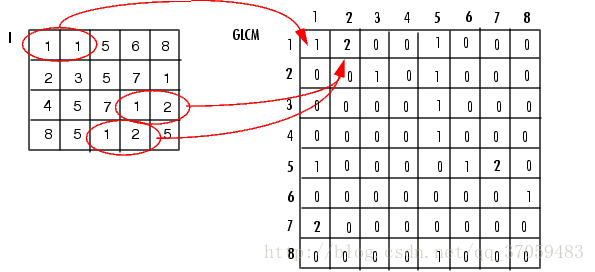
GLCMテーブルは、実際にはすべてのピクセルの可能な組み合わせです。たとえば、GLCM（1,1）はIのピクセル値1と1の組み合わせであり、GLCM（4,5）はIのピクセル4とピクセル5の組み合わせです。GLCM（i j）の値は、ピクセルがiで、ピクセルがjである隣接するポイントのペアの数です。この隣接にはルールがあります。f（x、y）、f（x + a、y + b）は隣接しています。つまり、xのみが単位で区切られ、yはb単位で区切られているため、隣接していると見なされます。
通常、隣接と言います。ポイントBはポイントAの右側にあり、実際、ここではa = 1、b = 0、つまりf（x、y）とf（x + 1、y + 0）が隣接しています。
だからあります：
a = 1、b = 0の場合、水平方向に隣接していると言います。つまり、0度の場合です。
a = 1、b = 1の場合、対角線が隣接している、つまり45度の場合
a = -1、b = 1の場合は135度
他の角度も同様です。
a = 1、b = 0の場合：GLCM（1,1）= 1;実際、Iには（1）に隣接する1と1がいくつかあります（上記の規則による）GLCM（1、2）= 2、いくつかの1と2が隣接しています（2）。 OK！
以下のプロパティの多くは、マトリックスが計算された後にこれに基づいて計算されます。それらは難しくありません！

追加の理解2：
共起行列は、2つの位置にあるピクセルの結合確率密度によって定義されます。これは、輝度の分布特性を反映するだけでなく、同じ輝度または輝度に近いピクセルの位置分布特性も反映します。これは、画像の輝度変化の2次統計機能です。。これは、一連のテクスチャ特性を定義するための基礎です。

テクスチャは空間内のグレーレベルの繰り返し発生によって形成されるため、画像空間内の特定の距離にある2つのピクセル間に特定のグレーレベルの関係、つまり画像内のグレーレベルの空間相関特性があります。グレーレベルの同時発生マトリックスは、グレーレベルの空間相関特性を研究することによってテクスチャを記述するための一般的な方法です。

グレースケールヒストグラムは、画像上の単一ピクセルの特定のグレースケールの統計結果です。

グレーレベルの同時発生マトリックスは、特定のグレーレベルで画像上の特定の距離を維持しながら2つのピクセルのステータスを統計的に計算することによって取得されます。

画像内の任意の点（x、y）（N×N）とそれから外れた別の点（x + a、y + b）を取り、この点のペアのグレー値を（g1、g2）に設定します。ポイント（x、y）を画面上で移動すると、さまざまな（g1、g2）値が取得されます。グレースケール値をkに設定すると、k ^ 2、（g1、g2）の組み合わせがあります。画面全体で、各（g1、g2）値の出現回数をカウントし、それらを正方形のマトリックスに配置します。（g1、g2）の出現総数を使用して、出現確率P（g1、 g2）、そのような正方形のマトリックスは、グレーレベルの同時発生マトリックスと呼ばれます。距離差の値（a、b）は、さまざまな数値の組み合わせを使用して、さまざまな条件下で結合確率行列を取得します。（A、b）テクスチャ周期分布の特性に応じて値を選択する必要があります。より細かいテクスチャの場合は、（1、0）、（1、1）、（2、0）などの小さな差の値が選択されます。 a = 1、b = 0の場合、ピクセルペアは水平、つまり0度スキャンです。a= 0、b = 1の場合、ピクセルペアは垂直、つまり90度スキャンです。a= 1、b = 1の場合、の場合、ピクセルペアは右に斜め、つまり45度のスキャンです。a= -1、b = -1の場合、ピクセルペアは左に斜め、つまり135度のスキャンです。
このようにして、2つのピクセルグレーレベルが同時に発生する確率は、（x、y）の空間座標を「グレーペア」（g1、g2）の記述に変換し、グレーレベル同時発生マトリックスを形成します。（バイドゥ百科事典）
画像のグレーレベル同時発生マトリックスは、方向、隣接する間隔、および変化の範囲に関する画像のグレーレベルの包括的な情報を反映できます。これは、画像のローカルパターンとその配置ルールを分析するための基礎となります。

ほぼ完了したように感じます！

グレーレベル共起マトリックスの特徴（文字がうまく書かれていないので、ご容赦ください）

2.1 コントラスト

測定マトリックスの値がどのように分布しているか、および画像の局所的な変化が画像の鮮明さとテクスチャの深さをどの程度反映しているか。テクスチャの溝が深いほど、コントラストが大きくなり、効果がはっきりします。逆に、コントラストが小さいほど、溝が浅くなり、効果がぼやけます。

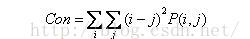
2.2 エネルギー

エネルギー変換は、画像のグレー分布とテクスチャの厚さの均一性を反映しています。グレーレベル共起行列の要素値が類似している場合、エネルギーは小さく、テクスチャが細かくなります。値の一部が大きく、他の値が小さい場合、エネルギー値は大きくなります。大きなエネルギー値は、より均一で規則的なテクスチャパターンを示します。

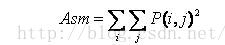
2.3 エントロピ

画像には、情報量のランダム性の尺度が含まれています。共起行列のすべての値が等しいか、ピクセル値が最大のランダム性を示す場合、エントロピーは最大になります。したがって、エントロピー値は画像のグレー分布の複雑さを示します。エントロピー値が大きいほど、画像は複雑になります。

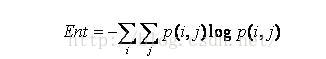
2.4 逆分散

逆分散は、画像テクスチャの局所的な変化のサイズを反映します。画像テクスチャのさまざまな領域がより均一でゆっくりと変化する場合、逆分散は大きくなり、その逆も同様です。

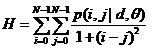
2.5 相関

これは、行または列方向の画像のグレーレベルの類似性を測定するために使用されます。したがって、値はローカルのグレー相関を反映します。値が大きいほど、相関が大きくなります。

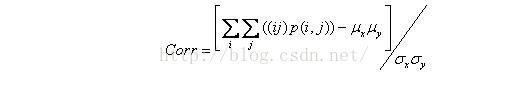
3、コード

#! /usr/bin/python
# - *- coding: UTF-8-*-import cv2
import math

# グレーレベルの最大数を定義します
gray_level =16

def maxGrayLevel(img):
 max_gray_level=0(height,width)=img.shape
 print("画像の高さと幅は次のとおりです。高さ,width",height,width)for y inrange(height):for x inrange(width):if img[y][x]> max_gray_level:
    max_gray_level = img[y][x]print("max_gray_level:",max_gray_level)return max_gray_level+1

def getGlcm(input,d_x,d_y):
 srcdata=input.copy()
 ret=[[0.0for i inrange(gray_level)]for j inrange(gray_level)](height,width)= input.shape

 max_gray_level=maxGrayLevel(input)
 # グレーレベルの数がグレーより大きい場合_レベル、画像のグレーレベルはグレーに減少します_レベル、グレーレベルの同時発生マトリックスのサイズを縮小します
 if max_gray_level > gray_level:for j inrange(height):for i inrange(width):
    srcdata[j][i]= srcdata[j][i]*gray_level / max_gray_level

 for j inrange(height-d_y):for i inrange(width-d_x):
   rows = srcdata[j][i]
   cols = srcdata[j + d_y][i+d_x]
   ret[rows][cols]+=1.0for i inrange(gray_level):for j inrange(gray_level):
   ret[i][j]/=float(height*width)return ret

def feature_computer(p):
 # con:コントラストは、画像の鮮明さとテクスチャの溝の深さを反映しています。テクスチャがシャープであるほど、コントラストが大きくなります。
 # eng:エントロピ,ENT）は、画像に含まれる情報量のランダム性を測定し、画像の複雑さを示します。共起行列のすべての値が等しいか、ピクセル値が最大のランダム性を示す場合、エントロピーが最大になります。
 # agm:角度2次モーメント（エネルギー）、画像の灰色分布とテクスチャの厚さの均一性の尺度。画像のテクスチャが均一で規則的である場合、エネルギー値は大きくなりますが、逆に、グレーレベルの共起行列の要素値は類似しており、エネルギー値は小さくなります。
 # idm:逆差行列は逆分散とも呼ばれ、テクスチャの明瞭さと規則性を反映しています。テクスチャは明確で規則的で、説明が簡単で、値が大きくなっています。
 Con=0.0
 Eng=0.0
 Asm=0.0
 Idm=0.0for i inrange(gray_level):for j inrange(gray_level):
   Con+=(i-j)*(i-j)*p[i][j]
   Asm+=p[i][j]*p[i][j]
   Idm+=p[i][j]/(1+(i-j)*(i-j))if p[i][j]>0.0:
    Eng+=p[i][j]*math.log(p[i][j])return Asm,Con,-Eng,Idm

def test(image_name):
 img = cv2.imread(image_name)try:
  img_shape=img.shape
 except:print('imread error')return

 # &#39;を使用する場合/&#39;TypeErrorを報告します: integer argument expected, got float
 # 実際、主なエラーはcv2によるものです.サイズ変更のパラメータは整数である必要があります
 img=cv2.resize(img,(img_shape[1]//2,img_shape[0]//2),interpolation=cv2.INTER_CUBIC)

 img_gray=cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

 glcm_0=getGlcm(img_gray,1,0)
 # glcm_1=getGlcm(src_gray,0,1)
 # glcm_2=getGlcm(src_gray,1,1)
 # glcm_3=getGlcm(src_gray,-1,1)print(glcm_0)

 asm,con,eng,idm=feature_computer(glcm_0)return[asm,con,eng,idm]if __name__=='__main__':
 result =test("/home/images/2019-05-27/8/20190527_17_29_03_X1_Y2.jpg")print(result)