Solve the problem of convex hull based on python
Recently I was reading a python algorithm book. I bought a book a year ago. I have been learning to recharge during work breaks. I finally saw this book, but it is indeed a bit difficult. I feel that the code written by the author is too dazzling. At that time, the comments were not very understandable. Finally, I thought of a method, that is, the algorithm problem mentioned in it. I used Baidu python to solve him. I think this is quite good.
**Below is a code for the convex hull problem. **
# - *- coding: utf-8-*-import turtle
import random
import time
f=open('point.txt','w')for i inrange(100):
x=random.randrange(-250,250,10)
y=random.randrange(-200,200,10)
f.write(str(x)+','+str(y)+'\n')
f.close()
point=[]
f=open('point.txt')for i in f:try:
temp=i.split(',')
x=float(temp[0]); y=float(temp[1])
point.append((x,y))
except :
print 'a err'
f.close()
point=list(set(point))#Remove duplicate points
n=0for i inrange(len(point)):if point[n][1] point[i][1]:
n=i
p0=point[n]
point.pop(n)
def compare(a,b):
x=[a[0]-p0[0],a[1]-p0[1]]
y=[b[0]-p0[0],b[1]-p0[1]]
dx=(x[0]**2+x[1]**2)**0.5
dy=(y[0]**2+y[1]**2)**0.5
cosa=x[0]/dx
cosb=y[0]/dy
if cosa < cosb:return1
elif cosa cosb:return-1else:if dx<dy:return-1
elif dx dy:return1else:return0
point.sort(compare)
point.insert(0,p0)
ep=point[:]#Copy elements, operation ep will not affect point
tag=0while tag==0:
tag=1
l=len(ep)for i inrange(l):
i1,i2,i3=(i,(i+1)%l,(i+2)%l)
x,y,z=(ep[i1],ep[i2],ep[i3])
a1,a2=((y[0]-x[0],y[1]-x[1]),(z[0]-y[0],z[1]-y[1]))if a1[0]*a2[1]-a1[1]*a2[0]<0:
tag=0
ep.pop(i2)break
elif a1[0]*a2[1]-a1[1]*a2[0]==0 and a1[0]*a2[0]<0:
#==0 Should be rewritten,360 degree situation
tag=0
ep.pop(i2)break
def drawpoint(point,color,line):
p=turtle.getturtle()
p.hideturtle()
turtle.delay(1)if(line=='p'):
p.speed(0)for i in point:
p.pu()
p.color(color)
p.goto(i)
p.pd()
p.dot()elif(line=='l'):
p.pu()
p.speed(1)for i in point:
p.color(color)
p.goto(i)
p.pd()
p.dot()
p.goto(point[0])drawpoint(point,'black','p')drawpoint(ep,'red','l')
time.sleep(1)
Supplementary knowledge: brute force algorithm and python implementation of convex hull problem
The basic idea of the brute force method is to first use the elimination method to determine the vertices of the convex hull, and then output these vertices in counterclockwise order. When judging whether the point P is a vertex on the convex hull, it has the following properties:
Given plane point set S, P, Pi, Pj, Pk are four different points in S, if P is located inside or on the boundary of the triangle formed by Pi, Pj, Pk, then P is not the convex hull vertex of S.
So how to judge the point P is inside or on the boundary of the triangle? Given two points AB on the plane, when the linear equation g(A,B,P)=0, P is on the straight line, and when g(A,B,P) 0 and g(A,B,P)<0, P respectively Located on both sides of the straight line.
To determine that the point P is inside or on the boundary of the triangle, it is only necessary to check whether P and each vertex of the triangle are on the same side of the line determined by the other two vertices of the triangle, that is, determine:
t1=g(pj,pk,p)*g(pj,pk,pi) =0 ,
t2=g(pi,pk,p)*g(pi,pk,pj) =0,
t3=g(pj,pi,p)*g(pj,pi,pk) =0
Are both established
The pseudo code of the brute force algorithm for the convex hull problem is as follows:
BruteForce(S):
Input: the set S of n points on the plane
Output: output all vertices of the convex hull of S in counterclockwise order
If n=3 Then output the vertices of S in counterclockwise order, the algorithm ends to find the point P with the smallest ordinate in S, which must be on the convex hull
Any three points Pi, Pj, Pk in For S Do If Pi, Pj, Pk One point is located in the triangle formed by the other two points and P. Then delete the point
Find the point A with the smallest abscissa and the point B with the smallest abscissa in S
Divide S into the point set SU above the line AB and the point set SL below the line AB. The two points A and B belong to SL
Sort SL in ascending order of abscissa, and output SL, SU in descending order of abscissa.
First randomly generate point set S
import random
import itertools
def generate_num(n):
random_list =list(itertools.product(range(1,100),range(1,100)))
lists=random.sample(random_list, n)return lists
Determine whether the point P is inside or on the boundary of the triangle, that is, whether the point P is on the convex hull
In the specific judgment process, especially when the coordinate points are dense, there are three more special cases
The two points forming a straight line are perpendicular to the x-axis
When the other three points except point P are on a straight line, point P should not be deleted, because point P may be a point on the convex hull at this time
When the other three points except point P are on a straight line and perpendicular to the x-axis, point P should not be deleted, because point P may be a point on the convex hull at this time
# Determine whether pi is located in pj,pk,p0 forms the triangle and returns t1,t2,t3 three variables
def isin(pi,pj,pk,p0):
x1 =float(p0[0])
x2 =float(pj[0])
x3 =float(pi[0])
x4 =float(pk[0])
y1 =float(p0[1])
y2 =float(pj[1])
y3 =float(pi[1])
y4 =float(pk[1])
k_j0=0
b_j0=0
k_k0=0
b_k0=0
k_jk=0
b_jk=0
perpendicular1=False
perpendicular2 = False
perpendicular3 = False
# pj,a straight line composed of p0, look at pi,whether pk is on the same side of the line
if x2 - x1 ==0:
# pj,When p0 constitutes a straight line perpendicular to the X axis
t1=(x3-x2)*(x4-x2)
perpendicular1=True
else:
k_j0 =(y2 - y1)/(x2 - x1)
b_j0 = y1 - k_j0 * x1
t1 =(k_j0 * x3 - y3 + b_j0)*(k_j0 * x4 - y4 + b_j0)
# pk,a straight line composed of p0, look at pi,whether pj is on the same side of the line
if x4 - x1 ==0:
# pk,When p0 constitutes a straight line perpendicular to the X axis
t2=(x3-x1)*(x2-x1)
perpendicular2=True
else:
k_k0 =(y4 - y1)/(x4 - x1)
b_k0 = y1 - k_k0 * x1
t2 =(k_k0 * x3 - y3 + b_k0)*(k_k0 * x2 - y2 + b_k0)
# pj,line composed of pk, look at pi,whether p0 is on the same side of the line
if x4 - x2 ==0:
# pj,When pk constitutes a straight line perpendicular to the X axis
t3=(x3-x2)*(x1-x2)
perpendicular3 = True
else:
k_jk =(y4 - y2)/(x4 - x2)
b_jk = y2 - k_jk * x2
t3 =(k_jk * x3 - y3 + b_jk)*(k_jk * x1 - y1 + b_jk)
# If pk, p0,pj, when the three points are in the same straight line, the point cannot be deleted
if(k_j0 * x4 - y4 + b_j0)==0and(k_k0 * x2 - y2 + b_k0)==0and(k_jk * x1 - y1 + b_jk)==0:
t1=-1
# If pk, p0,pj, when the three points are in the same straight line and perpendicular to the X axis, the point cannot be deleted
if perpendicular1 and perpendicular2 and perpendicular3:
t1=-1return t1,t2,t3
Next is the main part of the implementation algorithm, used to find the points on the convex hull
import isintriangle
def force(lis,n):
# When the number of points in the set S is 3, the set itself is the convex hull set
if n==3:return lis
else:
# The collection is sorted by ordinate, find the point p0 with the smallest y
lis.sort(key=lambda x: x[1])
p0=lis[0]
# Remove the remaining point set lis of p0_brute
lis_brute=lis[1:]
# temp is used to store the points that need to be deleted in the collection in lis_Index within brute. If one of the four points is inside the triangle formed by the remaining three points, then the point must not be a point on the convex hull
temp=[]
# The triple loop finds all such points in the triangle
for i inrange(len(lis_brute)-2):
pi=lis_brute[i]
# If the index i is already in temp, that is, pi must not be a point on the convex hull, skip this loop
if i in temp:continuefor j inrange(i+1,len(lis_brute)-1):
pj=lis_brute[j]
# If the index j is already in temp, that is, pj must not be a point on the convex hull, skip this loop
if j in temp:continuefor k inrange(j +1,len(lis_brute)):
pk=lis_brute[k]
# If the index k is already in temp, that is, pk must not be a point on the convex hull, skip this loop
if k in temp:continue
# Determine whether pi is in pj,pk,Inside the triangle formed by p0(it1,it2,it3)=isintriangle.isin(pi,pj,pk,p0)if it1 =0 and it2 =0 and it3 =0:if i not in temp:
temp.append(i)
# Determine whether pj is in pi,pk,Inside the triangle formed by p0(jt1,jt2,jt3)=isintriangle.isin(pj,pi,pk,p0)if jt1 =0 and jt2 =0 and jt3 =0:if j not in temp:
temp.append(j)
# Determine whether pk is in pj,pi,Inside the triangle formed by p0(kt1, kt2, kt3)= isintriangle.isin(pk, pi, pj, p0)if kt1 =0 and kt2 =0 and kt3 =0:if k not in temp:
temp.append(k)
# listlast is the finally selected convex hull set
lislast=[]for coor in lis_brute:
loc =[i for i, x inenumerate(lis_brute)if x == coor]for x in loc:
ploc = x
if ploc not in temp:
lislast.append(coor)
# Add p0 to the convex hull set
lislast.append(p0)return lislast
Finally, the output of the convex hull set is not much to say, it can be implemented according to the pseudo code. The convex hull brute force algorithm results in the point set size of 1000
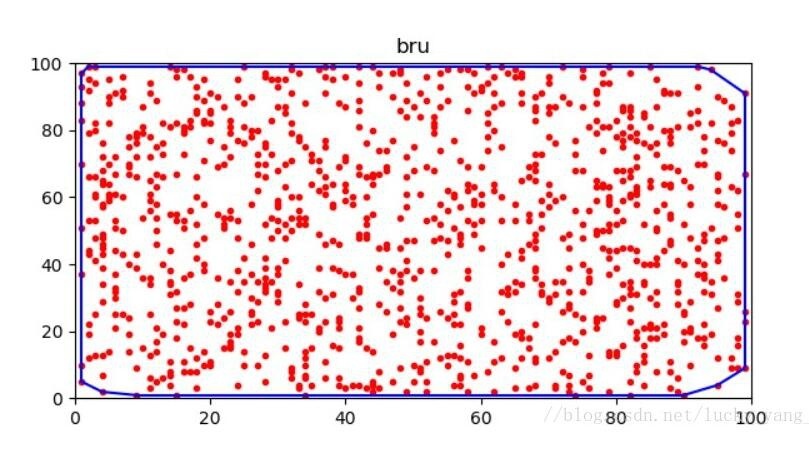
The above solution based on the python convex hull problem is all the content shared by the editor, I hope to give you a reference.
Recommended Posts