Gray-level co-occurrence matrix (with python code)

The theoretical content is quoted from https://blog.csdn.net/qq_37059483/article/details/78292869

Recently I am studying machine learning related content, and I will try my best to organize it into a series of blogs later. Then my friend asked me to help him implement an image quality evaluation method based on SVR support vector regression. However, I discovered at the beginning of the article
The unfamiliar guy, gray-level co-occurrence matrix, has this article.

Main reference blog 1: http://blog.csdn.net/jialeheyeshu/article/details/51337225
Main reference blog 2: http://blog.csdn.net/guanyuqiu/article/details/53117507
Main reference blog 3: http://www.cnblogs.com/rong86/p/3695621.html
Main reference blog 4: http://blog.csdn.net/lingtianyulong/article/details/53032034

1. Principle of Gray Level Co-occurrence Matrix Generation
   The statistical method of gray level co-occurrence matrix (GLDM) was proposed by R. Haralick et al. in the early 1970s. It is proposed on the premise that the spatial distribution relationship between pixels in the image contains image texture information. Extensive texture analysis method.

The gray-level co-occurrence matrix is defined as the probability of the gray value at a point leaving a fixed position (distance d, azimuth) starting from the pixel point with gray level i, that is, all estimated values can be expressed as The form of a matrix is called gray-level co-occurrence matrix. For images with slow texture changes, the value on the diagonal of the gray-level co-occurrence matrix is larger; for images with faster texture changes, the value on the diagonal of the gray-level co-occurrence matrix is smaller. The value is larger. Due to the large amount of data of the gray-level co-occurrence matrix, it is generally not directly used as a feature to distinguish texture, but based on some statistics constructed by it as a texture classification feature. Haralick once proposed 14 kinds of statistics calculated based on the gray level co-occurrence matrix: namely: energy, entropy, contrast, uniformity, correlation, variance, sum average, sum variance, sum entropy, difference variance, difference average, difference entropy , Related information measurement and maximum correlation coefficient.

**I have seen many examples of gray-level co-occurrence matrix generation on the Internet. I don’t feel like it is clear. Otherwise, I will directly upload the result or give a bunch of codes and formulas that I don’t understand. Later I read the introduction in matlab. In fact, It's very simple. Read the following three times carefully to understand how it came about! **(I understood the third article, I was very nervous at the time, I believe you will be fine)
The following figure shows how to solve the gray-level co-occurrence matrix. Taking the (1,1) point as an example, the GLCM(1,1) value of 1 means that only a pair of pixels with a gray level of 1 are horizontally adjacent. The GLCM(1, 2) value is 2 because there are two pairs of pixels with gray scales of 1 and 2 that are horizontally adjacent. (MatLab documentation)

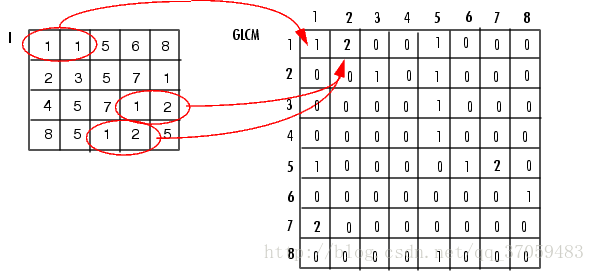
The GLCM table is actually the possible combination of all pixels. For example, GLCM(1,1) is the combination of pixel values 1 and 1 in I, GLCM(4,5) is the combination of pixel 4 and pixel 5 in I, GLCM(i The value of j) is the number of adjacent pairs of points where the pixel in I is i and the pixel is j. There is a rule for this adjacent: f(x,y),f(x+a,y+b) are adjacent, that is, only x is separated by a unit, y is separated by b units, we consider it adjacent.
Usually we say adjacent: point B is to the right of point A, in fact, here a=1, b=0, that is, f(x,y) and f(x+1,y+0) are adjacent.
So there is:
When a=1, b=0, we say horizontally adjacent: that is, when 0 degrees
When a=1, b=1, we say that the diagonals are adjacent, that is, when 45 degrees
a=-1, 135 degrees when b=1
Other angles are similar.
When a=1, b=0: GLCM(1,1)=1; in fact, there are several 1s and 1s adjacent (1) in I (according to the above rules) GLCM(1, 2)=2, Several 1 and 2 are adjacent (2). ok!
Many of the following properties are calculated on this basis after the matrix is calculated. Those are not difficult!

Additional understanding 2:
The co-occurrence matrix is defined by the joint probability density of pixels in two positions. It not only reflects the distribution characteristics of brightness, but also reflects the position distribution characteristics of pixels with the same brightness or close to the brightness. It is a second-order statistical feature of image brightness changes. . It is the basis for defining a set of texture characteristics.

Since the texture is formed by the repeated occurrence of grayscale in the spatial position, there will be a certain grayscale relationship between two pixels at a certain distance in the image space, that is, the spatial correlation characteristics of the grayscale in the image. Gray level co-occurrence matrix is a common method to describe texture by studying the spatial correlation characteristics of gray level.

Grayscale histogram is the statistical result of a certain grayscale of a single pixel on the image.

Take any point (x, y) in the image (N×N) and another point (x+a, y+b) that deviates from it, and set the gray value of this point pair to (g1, g2). If the point (x, y) is moved across the entire screen, various (g1, g2) values will be obtained. If the gray scale value is k, there are k^2; combinations of (g1, g2). For the entire screen, count the number of occurrences of each (g1, g2) value, and then arrange them into a square matrix, using the total number of occurrences of (g1, g2) to normalize them to the probability of occurrence P(g1, g2), such a square matrix is called a gray-level co-occurrence matrix. The distance difference value (a, b) takes different numerical combinations to obtain the joint probability matrix under different conditions. (A, b) The value should be selected according to the characteristics of the texture period distribution. For finer textures, small difference values such as (1, 0), (1, 1), (2, 0) are selected. When a=1, b=0, the pixel pair is horizontal, that is, 0-degree scanning; when a=0, b=1, the pixel pair is vertical, that is, 90-degree scanning; when a=1, b=1 When the pixel pair is diagonal to the right, that is, it is scanned at 45 degrees; when a=-1, b=-1, the pixel pair is diagonal to the left, that is, it scans at 135 degrees.
In this way, the probability of two pixel gray levels occurring at the same time transforms the spatial coordinates of (x, y) into a description of "gray pair" (g1, g2), forming a gray level co-occurrence matrix. (Baidu Encyclopedia)
The gray level co-occurrence matrix of an image can reflect the comprehensive information of the image gray level on the direction, the adjacent interval, and the range of change. It is the basis for analyzing the local patterns of the image and their arrangement rules.

It feels almost done!

2. Features of gray-level co-occurrence matrix (the characters are not well written, please forgive me)

2.1 Contrast

How the value of the metric matrix is distributed and how much local changes in the image reflect the sharpness of the image and the depth of the texture. The deeper the grooves of the texture, the greater the contrast, and the clearer the effect; on the contrary, the smaller the contrast, the shallower the grooves and the blurred effect.

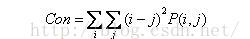
2.2 energy

Energy transformation reflects the uniformity of image gray distribution and texture thickness. If the element values of the gray-level co-occurrence matrix are similar, the energy is small, which means the texture is finer; if some of the values are large and the other values are small, the energy value is large. A large energy value indicates a more uniform and regular texture pattern.

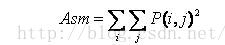
2.3 entropy

The image contains a measure of the randomness of the amount of information. When all the values in the co-occurrence matrix are equal or the pixel values show the greatest randomness, the entropy is the largest; therefore, the entropy value indicates the complexity of the image gray distribution. The larger the entropy value, the more complex the image.

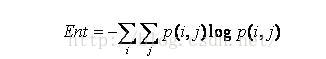
2.4 Inverse variance

The inverse variance reflects the size of the local changes in the image texture. If the different regions of the image texture are more uniform and change slowly, the inverse variance will be larger, and vice versa.

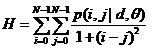
2.5 Correlation

It is used to measure the similarity of the gray level of the image in the row or column direction. Therefore, the value reflects the local gray correlation. The larger the value, the greater the correlation.

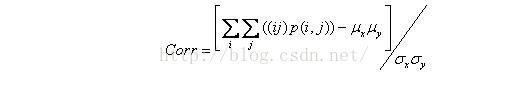
3、 Code

#! /usr/bin/python
# - *- coding: UTF-8-*-import cv2
import math

# Define the maximum number of gray levels
gray_level =16

def maxGrayLevel(img):
 max_gray_level=0(height,width)=img.shape
 print("The height and width of the image are: height,width",height,width)for y inrange(height):for x inrange(width):if img[y][x]> max_gray_level:
    max_gray_level = img[y][x]print("max_gray_level:",max_gray_level)return max_gray_level+1

def getGlcm(input,d_x,d_y):
 srcdata=input.copy()
 ret=[[0.0for i inrange(gray_level)]for j inrange(gray_level)](height,width)= input.shape

 max_gray_level=maxGrayLevel(input)
 # If the number of gray levels is greater than gray_level, the gray level of the image is reduced to gray_level, reduce the size of the gray-level co-occurrence matrix
 if max_gray_level > gray_level:for j inrange(height):for i inrange(width):
    srcdata[j][i]= srcdata[j][i]*gray_level / max_gray_level

 for j inrange(height-d_y):for i inrange(width-d_x):
   rows = srcdata[j][i]
   cols = srcdata[j + d_y][i+d_x]
   ret[rows][cols]+=1.0for i inrange(gray_level):for j inrange(gray_level):
   ret[i][j]/=float(height*width)return ret

def feature_computer(p):
 # con:Contrast reflects the sharpness of the image and the depth of the grooves of the texture. The sharper the texture, the greater the contrast, the greater the contrast.
 # eng:Entropy,ENT) measures the randomness of the amount of information contained in the image and expresses the complexity of the image. When all the values in the co-occurrence matrix are equal or the pixel values show the greatest randomness, the entropy is the largest.
 # agm:Angle second-order moment (energy), a measure of the uniformity of image gray distribution and texture thickness. When the image texture is uniform and regular, the energy value is large; on the contrary, the element values of the gray-level co-occurrence matrix are similar, and the energy value is small.
 # idm:The inverse difference matrix is also called the inverse variance, which reflects the clarity and regularity of the texture. The texture is clear, regular, easy to describe, and has a larger value.
 Con=0.0
 Eng=0.0
 Asm=0.0
 Idm=0.0for i inrange(gray_level):for j inrange(gray_level):
   Con+=(i-j)*(i-j)*p[i][j]
   Asm+=p[i][j]*p[i][j]
   Idm+=p[i][j]/(1+(i-j)*(i-j))if p[i][j]>0.0:
    Eng+=p[i][j]*math.log(p[i][j])return Asm,Con,-Eng,Idm

def test(image_name):
 img = cv2.imread(image_name)try:
  img_shape=img.shape
 except:print('imread error')return

 # If you use '/'Will report TypeError: integer argument expected, got float
 # In fact, the main error is because of cv2.The parameter in resize is required to be an integer
 img=cv2.resize(img,(img_shape[1]//2,img_shape[0]//2),interpolation=cv2.INTER_CUBIC)

 img_gray=cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

 glcm_0=getGlcm(img_gray,1,0)
 # glcm_1=getGlcm(src_gray,0,1)
 # glcm_2=getGlcm(src_gray,1,1)
 # glcm_3=getGlcm(src_gray,-1,1)print(glcm_0)

 asm,con,eng,idm=feature_computer(glcm_0)return[asm,con,eng,idm]if __name__=='__main__':
 result =test("/home/images/2019-05-27/8/20190527_17_29_03_X1_Y2.jpg")print(result)