最小二乗法とそのpython実装の詳細

分類回帰アルゴリズムの基礎としての最小二乗法には、長い歴史があります（1806年にMarie Legendreによって提案されました）。エラーの2乗の合計を最小化することにより、データの最適な関数一致を見つけます。最小二乗法を使用すると、未知のデータを簡単に取得し、取得したデータと実際のデータの間の誤差の二乗の合計を最小化できます。最小二乗法は、カーブフィッティングにも使用できます。他のいくつかの最適化の問題は、エネルギーを最小化するか、エントロピーを最大化することにより、最小二乗法で表現することもできます。

では、最小二乗法とは何ですか？心配しないでください。いくつかの簡単な概念から始めましょう。

一連のデータポイントがあるとします。

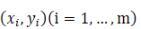
、次に、私たちが与えたフィッティング関数h（x）によって得られた推定値は次のようになります。

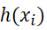
、それでは、私たちが与えたフィッティング関数と実際に解くべき関数との間の高度な適合性をどのように評価するのですか？ここで最初に概念を定義します：残差

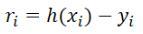
、適合度は残差に基づいていると推定します。さらに3つの基準があります。

•∞-ノルム：残差の絶対値の最大値

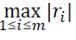
、これはすべてのデータポイント間の残留距離の最大値です

•1-ノルム：絶対残差の合計

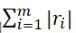
、これはすべてのデータポイントの残留距離の合計です

•2ノルム：残差二乗和

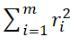
最初の2つの基準は、最も考えやすく、最も自然なものですが、差分操作を助長するものではありません。大量のデータの場合、計算量が多すぎて操作性がありません。したがって、一般的に2ノルムが使用されます。

そうは言っても、規範とフィッティングの関係は何ですか？適合度は、一般的には、適合関数h（x）と解くべき関数yの類似性です。次に、2ノルムが小さいほど、自然な類似性が高くなります。

これから、最小二乗法の定義を書くことができます。

与えられたデータについて

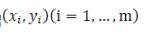
、与えられた仮説空間Hで、h（x）∈Hを解き、残差が

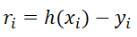
最小の2ノルム、つまり

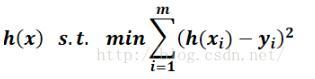
幾何学的に言えば、それは与えられたポイントを見つけることです

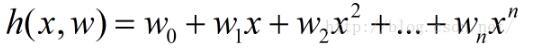
二乗距離の合計が最小の曲線y = h（x）。 h（x）はフィッティング関数または最小二乗解と呼ばれ、フィッティング関数h（x）を解く方法はカーブフィッティングの最小二乗法と呼ばれます。

では、h（x）はここでどのように見えるべきでしょうか？一般に、これは多項式曲線です。

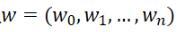
ここで、h（x、w）は次数nの多項式であり、wはそのパラメーターです。

言い換えれば、最小二乗法はそのようなグループを見つけることです

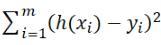
、作成

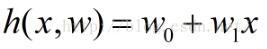
一番小さい。

では、そのフィッティング関数h（x）が目的関数yと最も高いフィッティング度を持つように、そのようなwを見つけるにはどうすればよいでしょうか。つまり、最小二乗法をどのように解くか、これが鍵となります。

フィッティング関数が線形関数であると仮定します。

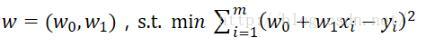
（もちろん、2次関数または高次元関数にすることもできます。これは単なる解決例であるため、最も単純な線形関数を使用します）次に、このようなwを見つけることが目標です。

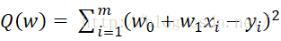
こちら注文

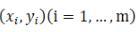
サンプルとして

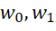
二乗損失関数

ここで、Q（w）は最適化するリスク関数です。

計算を学んだ学生はより明確になるはずです。これは極値を解く際の典型的な問題です。18の部分導関数を個別に見つけてから、部分導関数を0に設定するだけで、極値を見つけることができます。

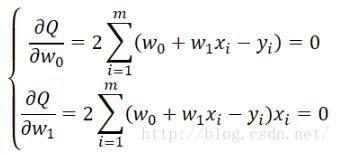
次に、w_iの値を解くには、この方程式系を解くだけです。

============ スプリットスプリット=============

上記では、最小二乗法とは何か、最小二乗解を解く方法について説明しました。以下では、Pythonを使用して最小二乗法を実装します。

ここでは、目的関数をy = sin（2πx）として選択し、正規分布をノイズ干渉として重ね合わせてから、多項式分布を使用してそれに適合させます。

コード：

# _*_ coding: utf-8 _*_
# 著者: yhao
# ブログ: http://blog.csdn.net/yhao2014
# メールボックス: [email protected]
 
import numpy as np #numpyを紹介します
import scipy as sp
import pylab as pl
from scipy.optimize import leastsq #最小二乗関数を導入する
 
n =9 #多項式度
 
 
# 目的関数
def real_func(x):return np.sin(2* np.pi * x)
 
 
# 多項式関数
def fit_func(p, x):
 f = np.poly1d(p)returnf(x)
 
 
# 残留機能
def residuals_func(p, y, x):
 ret =fit_func(p, x)- y
 return ret
 
 
x = np.linspace(0,1,9) #xとして9ポイントをランダムに選択
x_points = np.linspace(0,1,1000) #描画に必要な連続ポイント
 
y0 =real_func(x) #目的関数
y1 =[np.random.normal(0,0.1)+ y for y in y0] #正規分布ノイズを加えた後の機能
 
p_init = np.random.randn(n) #多項式パラメータをランダムに初期化します
 
plsq =leastsq(residuals_func, p_init, args=(y1, x))
 
print 'Fitting Parameters: ', plsq[0] #出力フィッティングパラメータ
 
pl.plot(x_points,real_func(x_points), label='real')
pl.plot(x_points,fit_func(plsq[0], x_points), label='fitted curve')
pl.plot(x, y1,'bo', label='with noise')
pl.legend()
pl.show()

出力フィッティングパラメータ：

画像は次のとおりです。

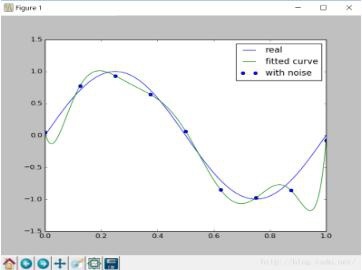
画像から、フィッティング関数がオーバーフィッティングしていることがわかります。次に、リスク関数に正規化項を追加して、オーバーフィッティングの現象を減らします。

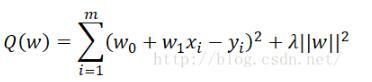
このために、残差関数で返された配列にlambda ^（1/2）pを追加するだけで済みます。

regularization =0.1 #正規化係数ラムダ
 
 
# 残留機能
def residuals_func(p, y, x):
 ret =fit_func(p, x)- y
 ret = np.append(ret, np.sqrt(regularization)* p) #ラムダ^(1/2)返された配列の後ろにpが追加されます
 return ret

出力フィッティングパラメータ：

画像は次のとおりです。

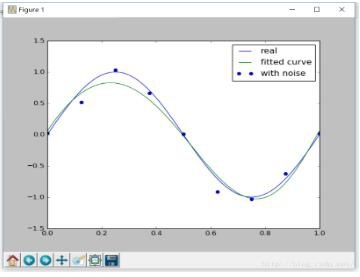
明らかに、適切な正規化の制約の下で、目的関数をより適切に適合させることができます。

正規化項の係数が大きすぎると、適合不足につながることに注意してください（この時点でのペナルティ項は特に重要です）

たとえば、regularization = 0.1を設定すると、イメージは次のようになります。

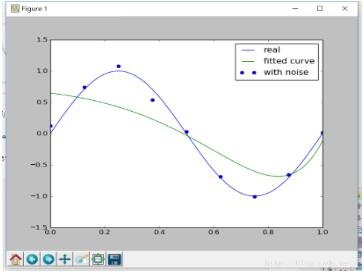
現時点では明らかに不十分です。したがって、正規化パラメータの選択は慎重に実行する必要があります。

最小二乗法とそのpython実装の上記の詳細な説明は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。