FMアルゴリズム分析とPython実装

**1. FMとは何ですか？ **

FMはFactorMachine、因数分解機の略です。

**2. なぜFMが必要なのですか？ **

1、 機能の組み合わせは、多くの機械学習モデリングプロセスで発生する問題です。機能を直接モデル化すると、機能と機能の間の関連情報が無視される可能性があります。したがって、新しいクロス機能機能の組み合わせを構築できます。モデルの効果を改善する方法。

2、 高次元のスパースマトリックスは、実際のエンジニアリングで一般的な問題であり、過度の計算とフィーチャの重みの更新の遅延に直接つながります。各列に8つの要素がある10000 * 100テーブルを想像してください。ワンホットエンコーディングの後、10000 * 800テーブルが生成されます。したがって、テーブルの各行には、1の値が100個、0の値が700個しかありません。

FMの利点は、これら2つの問題の処理にあります。 1つは特徴の組み合わせです。ペアワイズ特徴を組み合わせることにより、モデルスコアを向上させるためにクロスターム特徴が導入されます。2つ目は高次元の災害であり、特徴のパラメーター推定は隠しベクトル（パラメーターマトリックスのマトリックス分解）を導入することによって完了します。

**3. FMはどこで使用されますか？ **

FMが機能の組み合わせと高次元のスパースマトリックスの問題を解決できることはすでにわかっています。実際のビジネスシナリオでは、eコマース、Douban、およびその他の推奨システムのシナリオが最も広く使用されている領域です。たとえば、XiaoWangはDoubanのみを閲覧しています。 20本の映画があり、Doubanには20,000本の映画があります。XiaoWangに基づいて映画マトリックスを作成すると、199980個の要素がすべて0になることは間違いありません。そして、同様の問題はFMによって解決することができます。

**4. FMはどのように見えますか？ **

FMアルゴリズムを示す前に、最も一般的な線形式を確認しましょう。

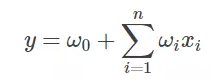
ここで、w0は初期の重み、またはバイアス項として理解され、wiは各特徴xiに対応する重みです。この線形式は、各機能と出力の間の関係のみを記述していることがわかります。

FMの式は次のとおりです。線形式の後に、新しいクロスターム特性と対応する重みのみが追加されていることがわかります。

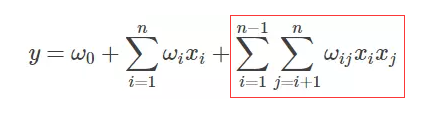
5. FM交差点の拡張

5.1 クロスタームを探しています###

FM式の解の核心は、クロスタームの解にあります。以下は、多くの人がクロスタームを解くために使用する拡張です。FMアルゴリズムに不慣れな人にとっては、疑問があるかもしれません。式を拡張する方法がわからない場合は、手動で導出します。

3つの変数（機能）x1 x2 x3があり、各機能の非表示変数はv1 =（1 2 3）、v2 =（4 5 6）、v3 =（1 2 1）です。

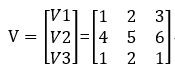
クロスタームで構成される重み行列Wを対称行列とします。対称行列として設定される理由は、対称行列をベクトルとベクトル転置で乗算できるためです。
次に、W = VVT、つまり

など：

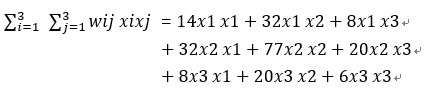
実際、考慮すべきクロスタームは、それ自体の組み合わせを除外するタームである必要があります。つまり、x1x1、x2x2、およびx3x3はクロスタームとは見なされず、実際のクロスタームはx1x2、x1x3、x2x1、x2x3、x3x1、x3x2です。
重複排除後のクロスタームは、x1x2、x1x3、およびx2x3です。これが、1/2が式に現れる理由です。

5.2 クロスアイテム重量変換###

クロスタームの基本を理解した後、n = 3を例として、式を以下に分解します。

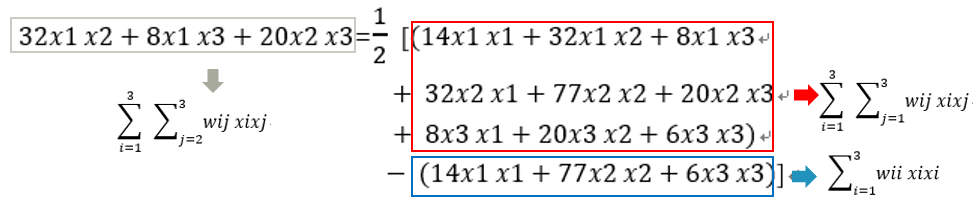
など：

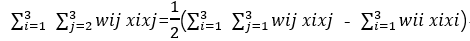
wijは次のように書くことができます

または

、viが1 * 3または3 * 1ベクトルであるかどうかによって異なります。

5.3 クロスターム拡張###

上記の例は、3つの機能のクロスターム導出であるため、n個の機能の場合、FMのクロスターム式は次のように一般化できます。

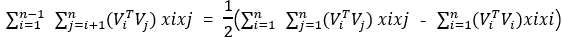
さらに分解することができます：

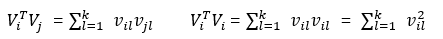
したがって、FMアルゴリズムのクロスタームは最終的に次のように拡張できます。

5.4 隠しベクトルvは埋め込みベクトルですか？###

トレーニングデータセットdataMatrixの形状が（20000、9）であり、1行のデータがサンプルiとして取得され、サンプルiの形状が（1、9）であり、非表示のベクトルviの形状が（9、8）であるとします（注：8はカスタム値で、埋め込みベクトルの長さを表します）

したがって、セクション5.3のクロスタームは次のように表すことができます。

sum((inter_1)^2 - (inter_2)^2)/2

その中で：

inter_1 = i * vの形状は（1、8）

inter_2 = np.multiply（i）* np.multiply（v）形状は（1、8）

クロスタームでサンプルiを計算した後、ベクトル形状が（1、8）のinter_1とinter_2が得られていることがわかります。

寸法が小さくなるため、この計算プロセスは、クロスタームにサンプルiの*埋め込みベクトル変換とほぼ見なすことができます。 *

したがって、以前の理解を変更する必要があります。

1. 私たちの口の中に隠されたベクトルviは実際にはベクトルグループであり、その形状は（入力フィーチャの後の長さワンホット、カスタム長さ）です;
2. 隠しベクトルviは埋め込みベクトルを表しませんが、入力上の埋め込みベクトルのベクトルグループを表します。これは重み行列としても理解できます。
3. i * viを入力して得られるベクトルは、実際の埋め込みベクトルです。

具体的には、ノード7のコード実装と併せて理解することができます。

6. 重量解決

勾配降下法を使用して、特徴（入力項目）に対する損失関数の導関数を計算することによって勾配が計算され、それによって重みが更新されます。 mをサンプル数、θを重量とします。

それが回帰問題である場合、損失関数は一般に平均二乗誤差（MSE）です。

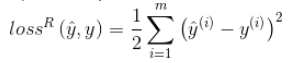
したがって、回帰問題の損失関数の重みに対する勾配（導関数）は次のようになります。

それがバイナリ分類の問題である場合、損失関数は一般にロジット損失です。

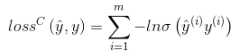
その中で、

ステップ関数Sigmoidを表します。

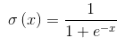
したがって、分類問題の重みに対する損失関数の勾配（導関数）は次のようになります。

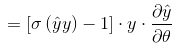
** これに対応して、定数項、1次項、および相互項**の導関数はそれぞれ次のとおりです。

7. FMアルゴリズムのPython実装

FMアルゴリズムのPython実装フローチャートは次のとおりです。

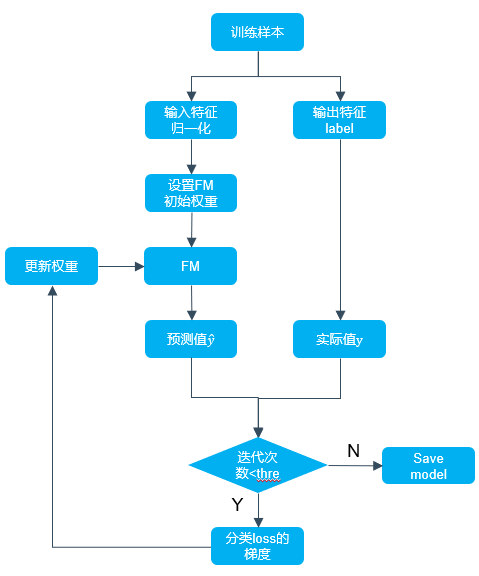
次の4つの点に注意する必要があります。

1. バイアス項の重みw0、一次項の重みw、およびクロス項の補助ベクトルの初期化を含む初期化パラメーター。

2. FMアルゴリズムを定義します。

3. 損失関数の勾配の定義。

4. 勾配降下を使用してパラメータを更新します。

次のコードスニペットは、上記の4つのポイントの説明です。ここで、損失は2つの分類の損失損失ではなく、分類損失の勾配の一部です。

• loss = self.sigmoid(classLabels[x] * p[0, 0]) -1*

実際、2つのカテゴリの損失損失の勾配は次のように表すことができます。

• gradient = (self.sigmoid(classLabels[x] * p[0, 0]) -1)*classLabels[x]p_derivative

その中で、p_derivativeは、定数項、1次項、および相互項の導関数を表します（詳細については、この記事のセクション6を参照してください）。

FMアルゴリズムコードスニペット

1   # 初期化パラメータ
 2   w =zeros((n,1))  #ここで、nは機能の数です。
 3   w_0 =0.4         v =normalvariate(0,0.2)*ones((n, k))5for it inrange(self.iter): #反復回数
 6    # サンプルごとに最適化
 7 for x inrange(m):8                 #ここで数学的な知識に注意してください。ドット積に対応する場所には通常合計があり、位置積に対応する場所には通常ありません。詳細については、マトリックス操作ルールを参照してください。ここでの計算ロジックは次のとおりです。http://blog.csdn.net/google19890102/article/details/455327459                 # xi·vi,xiとviのマトリックスドット積
10     inter_1 = dataMatrix[x]* v
11     # xiとxiとxiの対応する位置の積^2とvi^2対応する位置の積のドット積
12     inter_2 =multiply(dataMatrix[x], dataMatrix[x])*multiply(v, v)  #multiplymultiply対応する要素
13     # 完全なクロスターム,xi*vi*xi*vi - xi^2*vi^214                 interaction =sum(multiply(inter_1, inter_1)- inter_2)/2.15                 #予測出力を計算する
16     p = w_0 + dataMatrix[x]* w + interaction
17 print('classLabels[x]:',classLabels[x])18print('予測出力p:', p)19                 #シグモイドを計算する(y*pred_y)-1正確に言えば、損失ではありません。元の作者は、ここに問題があることを理解しています。これは、wを更新するための中間パラメーターとしてのみ使用されます。大きいほど良いほど大きくなりますが、以下では、勾配上昇の代わりに勾配下降を使用します。
20     loss = self.sigmoid(classLabels[x]* p[0,0])-121if loss >=-1:22                     loss_res ='正の方向'23else:24                     loss_res ='反対方向'25                 #パラメータを更新します
26     w_0 = w_0 - self.alpha * loss * classLabels[x]27for i inrange(n):28if dataMatrix[x, i]!=0:29                         w[i,0]= w[i,0]- self.alpha * loss * classLabels[x]* dataMatrix[x, i]30for j inrange(k):31                             v[i, j]= v[i, j]- self.alpha * loss * classLabels[x]*(32                                     dataMatrix[x, i]* inter_1[0, j]- v[i, j]* dataMatrix[x, i]* dataMatrix[x, i])

FMアルゴリズムの完全な実装

1 # - *- coding: utf-8-*-23from __future__ import division
 4 from math import exp
 5 from numpy import*6from random import normalvariate  #正規分布
 7 from sklearn import preprocessing
 8 import numpy as np
  910'''
 11  data :データ経路
 12  feature_potenital :潜在的な分解次元の数
 13  アルファ：学習率
 14  iter：反復回数
 15  _ w,_w_0,_v：分割されたサブマトリックスの重み
 16  with_col :列付き_name
 17  first_col :貴重な機能の最初の列のインデックス
 18'''
 192021 classfm(object):22     def __init__(self):23         self.data = None
 24   self.feature_potential = None
 25   self.alpha = None
 26   self.iter = None
 27   self._w = None
 28   self._w_0 = None
 29   self.v = None
 30   self.with_col = None
 31   self.first_col = None
 3233  def min_max(self, data):34         self.data = data
 35   min_max_scaler = preprocessing.MinMaxScaler()36return min_max_scaler.fit_transform(self.data)3738     def loadDataSet(self, data, with_col=True, first_col=2):39         #私はただ遊んでいる、pd.read_table()直接行うことができ、コードが非常に長いようで、小さなデータの下で直接読み取ることができます、悲しいかな〜
 40   self.first_col = first_col
 41   dataMat =[]42         labelMat =[]43         fr =open(data)44         self.with_col = with_col
 45 if self.with_col:46             N =047for line in fr.readlines():48                 # N=1でリスト名を殺す
 49 if N >0:50                     currLine = line.strip().split()51                     lineArr =[]52                     featureNum =len(currLine)53for i inrange(self.first_col, featureNum):54                         lineArr.append(float(currLine[i]))55                     dataMat.append(lineArr)56                     labelMat.append(float(currLine[1])*2-1)57                 N = N +158else:59for line in fr.readlines():60                 currLine = line.strip().split()61                 lineArr =[]62                 featureNum =len(currLine)63for i inrange(2, featureNum):64                     lineArr.append(float(currLine[i]))65                 dataMat.append(lineArr)66                 labelMat.append(float(currLine[1])*2-1)67returnmat(self.min_max(dataMat)), labelMat
 6869  def sigmoid(self, inx):70         # return1.0/(1+exp(min(max(-inx,-10),10)))71return1.0/(1+exp(-inx))7273     #対応するフィーチャウェイトマトリックスを取得します
 74  def fit(self, data, feature_potential=8, alpha=0.01, iter=100):75         #アルファは学習率です
 76   self.alpha = alpha
 77   self.feature_potential = feature_potential
 78   self.iter = iter
 79   # dataMatrixはマットを使用します,classLabelsはリストです
 80   dataMatrix, classLabels = self.loadDataSet(data)81print('dataMatrix:',dataMatrix.shape)82print('classLabels:',classLabels)83         k = self.feature_potential
 84   m, n =shape(dataMatrix)85         #初期化パラメータ
 86   w =zeros((n,1))  #ここで、nは機能の数です。
 87   w_0 =0.88         v =normalvariate(0,0.2)*ones((n, k))89for it inrange(self.iter): #反復回数
 90    # サンプルごとに最適化
 91 for x inrange(m):92                 #ここで数学的な知識に注意してください。ドット積に対応する場所には通常合計があり、位置積に対応する場所には通常ありません。詳細については、マトリックス操作ルールを参照してください。ここでの計算ロジックは次のとおりです。http://blog.csdn.net/google19890102/article/details/4553274593                 # xi·vi,xiとviのマトリックスドット積
 94     inter_1 = dataMatrix[x]* v
 95     # xiとxiとxiの対応する位置の積^2とvi^2対応する位置の積のドット積
 96     inter_2 =multiply(dataMatrix[x], dataMatrix[x])*multiply(v, v)  #multiplymultiply対応する要素
 97     # 完全なクロスターム,xi*vi*xi*vi - xi^2*vi^298                 interaction =sum(multiply(inter_1, inter_1)- inter_2)/2.99                 #予測出力を計算する
100     p = w_0 + dataMatrix[x]* w + interaction
101 print('classLabels[x]:',classLabels[x])102print('予測出力p:', p)103                 #シグモイドを計算する(y*pred_y)-1104                 loss = self.sigmoid(classLabels[x]* p[0,0])-1105if loss >=-1:106                     loss_res ='正の方向'107else:108                     loss_res ='反対方向'109                 #パラメータを更新します
110     w_0 = w_0 - self.alpha * loss * classLabels[x]111for i inrange(n):112if dataMatrix[x, i]!=0:113                         w[i,0]= w[i,0]- self.alpha * loss * classLabels[x]* dataMatrix[x, i]114for j inrange(k):115                             v[i, j]= v[i, j]- self.alpha * loss * classLabels[x]*(116                                     dataMatrix[x, i]* inter_1[0, j]- v[i, j]* dataMatrix[x, i]* dataMatrix[x, i])117print('the no %s times, the loss arrach %s'%(it, loss_res))118         self._w_0, self._w, self._v = w_0, w, v
119120  def predict(self, X):121if(self._w_0 == None)or(self._w == None).any()or(self._v == None).any():122             raise NotFittedError("Estimator not fitted, call `fit` first")123         #タイプチェック
124 ifisinstance(X, np.ndarray):125             pass
126 else:127try:128                 X = np.array(X)129             except:130                 raise TypeError("numpy.ndarray required for X")131         w_0 = self._w_0
132   w = self._w
133   v = self._v
134   m, n =shape(X)135         result =[]136for x inrange(m):137             inter_1 =mat(X[x])* v
138    inter_2 =mat(multiply(X[x], X[x]))*multiply(v, v)  #multiplymultiply対応する要素
139    # 完全なクロスターム
140    interaction =sum(multiply(inter_1, inter_1)- inter_2)/2.141             p = w_0 + X[x]* w + interaction  #予測出力を計算する
142    pre = self.sigmoid(p[0,0])143             result.append(pre)144return result
145146  def getAccuracy(self, data):147         dataMatrix, classLabels = self.loadDataSet(data)148         w_0 = self._w_0
149   w = self._w
150   v = self._v
151   m, n =shape(dataMatrix)152         allItem =0153         error =0154         result =[]155for x inrange(m):156             allItem +=1157             inter_1 = dataMatrix[x]* v
158    inter_2 =multiply(dataMatrix[x], dataMatrix[x])*multiply(v, v)  #multiplymultiply対応する要素
159    # 完全なクロスターム
160    interaction =sum(multiply(inter_1, inter_1)- inter_2)/2.161             p = w_0 + dataMatrix[x]* w + interaction  #予測出力を計算する
162    pre = self.sigmoid(p[0,0])163             result.append(pre)164if pre <0.5 and classLabels[x]==1.0:165                 error +=1166             elif pre >=0.5 and classLabels[x]==-1.0:167                 error +=1168else:169continue170         # print(result)171         value =1-float(error)/ allItem
172 return value
173174175 classNotFittedError(Exception):176"""
177  Exception classto raise if estimator is used before fitting
178"""
179  pass
180181182 if __name__ =='__main__':183fm()