交差点のPython実装とIOUチュートリアル

ターゲット検出で使用される概念であるIntersection-over-Union（IoU）は、生成された候補境界とグラウンドトゥルース境界、つまりそれらの交差と結合の間のオーバーラップ率です。セットの比率。理想的な状況は完全なオーバーラップです。つまり、比率は1です。

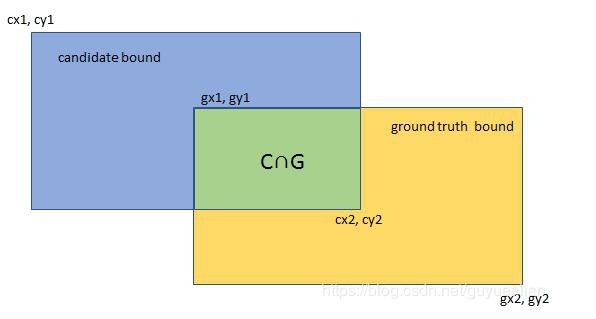
計算式：

Python実装コード：

def cal_iou(box1, box2):"""
 : param box1:=[xmin1, ymin1, xmax1, ymax1]:param box2:=[xmin2, ymin2, xmax2, ymax2]:return:"""
 xmin1, ymin1, xmax1, ymax1 = box1
 xmin2, ymin2, xmax2, ymax2 = box2
 # 各長方形の面積を計算します
 s1 =(xmax1 - xmin1)*(ymax1 - ymin1) #Cのエリア
 s2 =(xmax2 - xmin2)*(ymax2 - ymin2) #Gエリア
 
 # 交差する長方形を計算する
 xmin =max(xmin1, xmin2)
 ymin =max(ymin1, ymin2)
 xmax =min(xmax1, xmax2)
 ymax =min(ymax1, ymax2)
 
 w =max(0, xmax - xmin)
 h =max(0, ymax - ymin)
 area = w * h #C∩Gエリア
 iou = area /(s1 + s2 - area)return iou

# - *- coding: utf-8-*-"""
 @ Project: IOU
 @ File : IOU.py
 @ Author : panjq
 @ E-mail : [email protected]
 @ Date :2018-10-1410:44:06"""
def calIOU_V1(rec1, rec2):"""
 computing IoU
 : param rec1:(y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2:(y0, x0, y1, x1):return: scala value of IoU
 """
 # 各長方形の面積を計算します
 S_rec1 =(rec1[2]- rec1[0])*(rec1[3]- rec1[1])
 S_rec2 =(rec2[2]- rec2[0])*(rec2[3]- rec2[1])
 
 # computing the sum_area
 sum_area = S_rec1 + S_rec2
 
 # find the each edge of intersect rectangle
 left_line =max(rec1[1], rec2[1])
 right_line =min(rec1[3], rec2[3])
 top_line =max(rec1[0], rec2[0])
 bottom_line =min(rec1[2], rec2[2])
 
 # judge if there is an intersect
 if left_line  = right_line or top_line  = bottom_line:return0else:
 intersect =(right_line - left_line)*(bottom_line - top_line)return intersect/(sum_area - intersect)
 
def calIOU_V2(rec1, rec2):"""
 computing IoU
 : param rec1:(y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2:(y0, x0, y1, x1):return: scala value of IoU
 """
 # cx1 = rec1[0]
 # cy1 = rec1[1]
 # cx2 = rec1[2]
 # cy2 = rec1[3]
 # gx1 = rec2[0]
 # gy1 = rec2[1]
 # gx2 = rec2[2]
 # gy2 = rec2[3]
 cx1,cy1,cx2,cy2=rec1
 gx1,gy1,gx2,gy2=rec2
 # 各長方形の面積を計算します
 S_rec1 =(cx2 - cx1)*(cy2 - cy1) #Cのエリア
 S_rec2 =(gx2 - gx1)*(gy2 - gy1) #Gエリア
 
 # 交差する長方形を計算する
 x1 =max(cx1, gx1)
 y1 =max(cy1, gy1)
 x2 =min(cx2, gx2)
 y2 =min(cy2, gy2)
 
 w =max(0, x2 - x1)
 h =max(0, y2 - y1)
 area = w * h #C∩Gエリア
 
 iou = area /(S_rec1 + S_rec2 - area)return iou
 
if __name__=='__main__':
 rect1 =(661,27,679,47)
 # ( top, left, bottom, right)
 rect2 =(662,27,682,47)
 iou1 =calIOU_V1(rect1, rect2)
 iou2 =calIOU_V2(rect1, rect2)print(iou1)print(iou2)

参照：https：//www.zalou.cn/article/184542.htm

補足知識：Pythonは、Precision、Recall、f1-score、mIOU、その他の指標など、複数のカテゴリの混同行列を計算します

コードに直接移動すると、一目でわかります

import os
import numpy as np
from glob import glob
from collections import Counter
 
def cal_confu_matrix(label, predict, class_num):
 confu_list =[]for i inrange(class_num):
 c =Counter(predict[np.where(label == i)])
 single_row =[]for j inrange(class_num):
 single_row.append(c[j])
 confu_list.append(single_row)return np.array(confu_list).astype(np.int32)
 
 
def metrics(confu_mat_total, save_path=None):'''
 : param confu_mat:総混乱マトリックス
 背景：背景を殺すかどうか
 : return:txtは混乱マトリックスを書き出す, precision，recall，IOU，f-score
 '''
 class_num = confu_mat_total.shape[0]
 confu_mat = confu_mat_total.astype(np.float32)+0.0001
 col_sum = np.sum(confu_mat, axis=1) #行ごとの合計
 raw_sum = np.sum(confu_mat, axis=0) #各列の数
 
 ''' さまざまな面積比を計算してOA値を見つけます'''
 oa =0for i inrange(class_num):
 oa = oa + confu_mat[i, i]
 oa = oa / confu_mat.sum()'''Kappa'''
 pe_fz =0for i inrange(class_num):
 pe_fz += col_sum[i]* raw_sum[i]
 pe = pe_fz /(np.sum(confu_mat)* np.sum(confu_mat))
 kappa =(oa - pe)/(1- pe)
 
 # 混乱マトリックスをexcelに書き込む
 TP =[] #認識されている各カテゴリの正しい分類の数
 
 for i inrange(class_num):
 TP.append(confu_mat[i, i])
 
 # f1を計算する-score
 TP = np.array(TP)
 FN = col_sum - TP
 FP = raw_sum - TP
 
 # 精度を計算して書き出す、思い出す, f1-score，f1-mとmIOU
 
 f1_m =[]
 iou_m =[]for i inrange(class_num):
 # f1を書く-score
 f1 = TP[i]*2/(TP[i]*2+ FP[i]+ FN[i])
 f1_m.append(f1)
 iou = TP[i]/(TP[i]+ FP[i]+ FN[i])
 iou_m.append(iou)
 
 f1_m = np.array(f1_m)
 iou_m = np.array(iou_m)if save_path is not None:withopen(save_path +'accuracy.txt','w')as f:
 f.write('OA:\t%.4f\n'%(oa*100))
 f.write('kappa:\t%.4f\n'%(kappa*100))
 f.write('mf1-score:\t%.4f\n'%(np.mean(f1_m)*100))
 f.write('mIou:\t%.4f\n'%(np.mean(iou_m)*100))
 
 # 書き込み精度
 f.write('precision:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(TP[i]/raw_sum[i])*100))
 f.write('\n')
 
 # リコールを書く
 f.write('recall:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(TP[i]/ col_sum[i])*100))
 f.write('\n')
 
 # f1を書く-score
 f.write('f1-score:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(f1_m[i])*100))
 f.write('\n')
 
 # IOUを書き出す
 f.write('Iou:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(iou_m[i])*100))
 f.write('\n')

上記のpythonの実装と比較のIOUチュートリアルは、エディターによって共有されるすべてのコンテンツです。参考にしてください。