Pythonの基本的な描画チュートリアル(2つ)

今回はパイソンベーシックドローイングの第2号です。最近、編集者がインストラクターのプッシュでいくつかのグラフィックスドローイングを学び、急いで共有しました。
1. スキャッターチャート
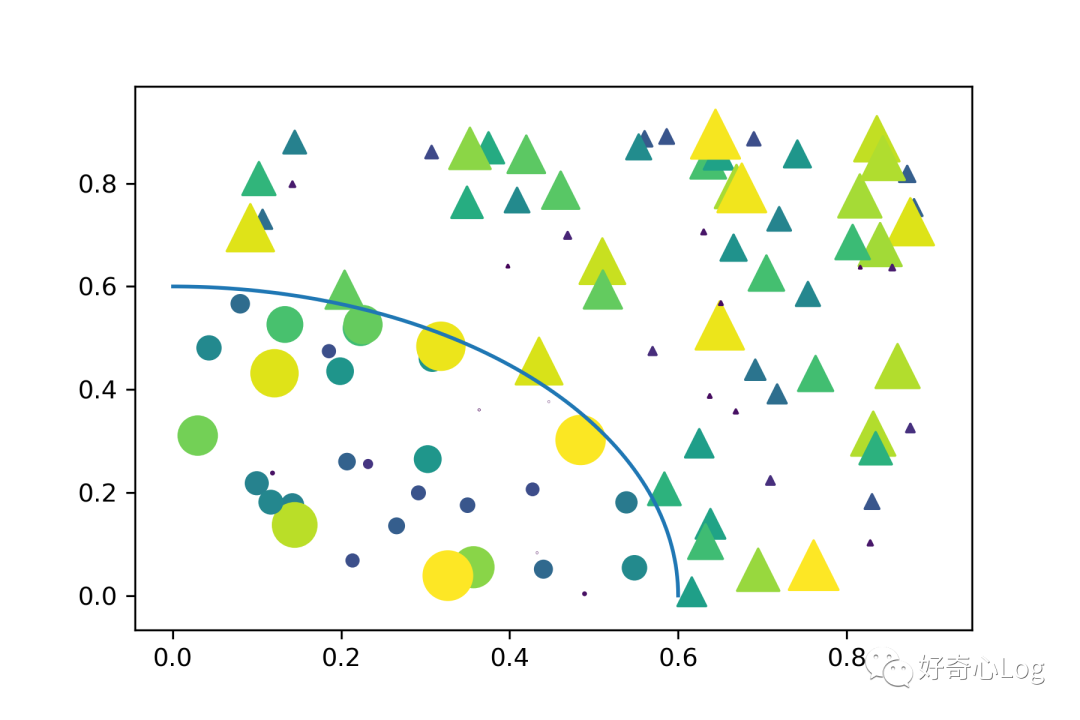
import matplotlib.pyplot as plt
import numpy as np
# Fixing random state for reproducibility
np.random.seed(19680801)
fig = plt.figure()
N =100
r0 =0.6
x =0.9* np.random.rand(N)
y =0.9* np.random.rand(N)
area =(20* np.random.rand(N))**2 # 0 to 10 point radii
c = np.sqrt(area)
r = np.sqrt(x **2+ y **2)
area1 = np.ma.masked_where(r < r0, area)
area2 = np.ma.masked_where(r >= r0, area)
plt.scatter(x, y, s=area1, marker='^', c=c)
plt.scatter(x, y, s=area2, marker='o', c=c)
# Show the boundary between the regions:
theta = np.arange(0, np.pi /2,0.01)
plt.plot(r0 * np.cos(theta), r0 * np.sin(theta))
plt.show()
2. 円グラフ ##
fig, ax = plt.subplots(figsize=(6,3), subplot_kw=dict(aspect="equal"))
recipe =["SST","SLP","UWND","VWND","HFLUX","PRECIPITATION"]
data =[0.34,0.16,0.22,0.05,0.08,0.15]
wedges, texts = ax.pie(data, wedgeprops=dict(width=0.5), startangle=-40)
bbox_props =dict(boxstyle="square,pad=0.3", fc="w", ec="k", lw=0.72)
kw =dict(arrowprops=dict(arrowstyle="-"),
bbox=bbox_props, zorder=0, va="center")for i, p inenumerate(wedges):
ang =(p.theta2 - p.theta1)/2.+ p.theta1
y = np.sin(np.deg2rad(ang))
x = np.cos(np.deg2rad(ang))
horizontalalignment ={-1:"right",1:"left"}[int(np.sign(x))]
connectionstyle ="angle,angleA=0,angleB={}".format(ang)
kw["arrowprops"].update({"connectionstyle": connectionstyle})
ax.annotate(recipe[i], xy=(x, y), xytext=(1.35*np.sign(x),1.4*y),horizontalalignment=horizontalalignment,**kw)
ax.set_title("Weight proportion")
plt.show()
3. 風の場のベクトル図
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5,5,5)
X, Y = np.meshgrid(x, x)
U, V =12* X,12* Y
data =[(-1.5,.5,-6,-6),(1,-1,-46,46),(-3,-1,11,-11),(1,1.5,80,80),(0.5,0.25,25,15),(-1.5,-0.5,-5,40)]
data = np.array(data, dtype=[('x', np.float32),('y', np.float32),('u', np.float32),('v', np.float32)])
fig1, axs1 = plt.subplots(nrows=2, ncols=2)
# Default parameters, uniform grid
axs1[0,0].barbs(X, Y, U, V)
# Arbitrary setof vectors, make them longer and change the pivot point
# ( point around which they're rotated) to be the middle
axs1[0,1].barbs(
data['x'], data['y'], data['u'], data['v'], length=8, pivot='middle')
# Showing colormapping with uniform grid. Fill the circle for an empty barb,
# don't round the values, and change some of the size parameters
axs1[1,0].barbs(
X, Y, U, V, np.sqrt(U **2+ V **2), fill_empty=True, rounding=False,
sizes=dict(emptybarb=0.25, spacing=0.2, height=0.3))
# Change colors as well as the increments for parts of the barbs
axs1[1,1].barbs(data['x'], data['y'], data['u'], data['v'], flagcolor='r',
barbcolor=['b','g'], flip_barb=True,
barb_increments=dict(half=10, full=20, flag=100))
# Masked arrays are also supported
masked_u = np.ma.masked_array(data['u'])
masked_u[4]=1000 # Bad value that should not be plotted when masked
masked_u[4]= np.ma.masked
fig1.savefig("/Users/chenyue/Downloads/f7.png",dpi=300)
plt.show()
4. 3 D画像
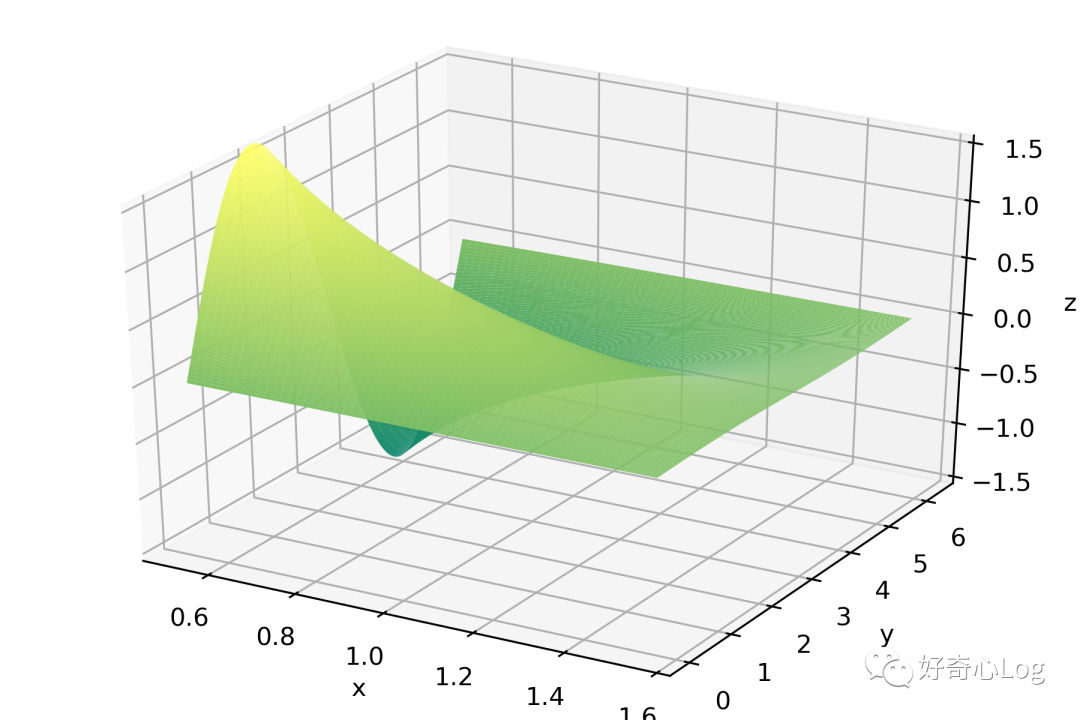
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
X = np.arange(30*np.pi/180,89*np.pi/180, np.pi/180)
Y = np.arange(0,360*np.pi/180, np.pi/180)
X, Y = np.meshgrid(X, Y)
Z = np.sin(Y)/np.tan(X)
fig = plt.figure()
ax =Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='summer')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_zlim(-1.5,1.5)
plt.show()
これでこの号の紹介は終わりです。記事のコードは水平方向にスワイプできます。実際の操作に便利なように、関連するコードとサンプルはBaiduネットワークディスクに保存されています。リンク:https://pan.baidu.com/s/1uSGDqbeCAh1ZS -dz-zs5tA抽出コード:8n9x、読者や友人はダウンロードして学ぶことができます。
参照リンク
https://matplotlib.org/gallery/index.html
このエディターの号が読者や友人の助けになり、もっと練習することを忘れないでください。
Recommended Posts