Python一次元二次元補間の例

一次元補間

補間はフィッティングとは異なります。補間関数はサンプルポイントを通過し、フィッティング関数は通常、すべてのサンプルポイントにできるだけ近い最小二乗法に基づいています。一般的な補間方法には、ラグランジュ補間、セグメント補間、スプライン補間などがあります。

ラグランジュ補間多項式：ノード数nが多い場合、ラグランジュ補間多項式の次数が高くなり、収束に矛盾が生じ、計算が複雑になります。サンプルポイントの増加に伴い、高次補間で誤差が生じる振動現象をルンゲ現象と呼びます。

ピースワイズ補間：収束しますが、滑らかさが劣ります。

スプライン補間：スプライン補間は、スプラインと呼ばれる特別なピースワイズ多項式を使用した補間の形式です。スプライン補間では、低次の多項式スプラインを使用して補間誤差を小さくすることができ、高次の多項式を使用するときに発生するルンジ現象を回避できるため、スプライン補間が一般的になりました。

CODEでコードピースを表示し、私のコードピースから派生

#! /usr/bin/env python 
# - *- coding:utf-8-*-import numpy as np 
from scipy import interpolate 
import pylab as pl 
 
x=np.linspace(0,10,11) 
# x=[0.1.2.3.4.5.6.7.8.9.10.] 
y=np.sin(x) 
xnew=np.linspace(0,10,101) 
pl.plot(x,y,"ro")for kind in["nearest","zero","slinear","quadratic","cubic"]:#補間法
 #" nearest","zero"ステップを補間する
 # 線形線形補間
 #" quadratic","cubic"2番目と3番目のBスプライン曲線を補間します
 f=interpolate.interp1d(x,y,kind=kind) 
 # ‘slinear', ‘quadratic' and ‘cubic' refer to a spline interpolation of first, second or third order) 
 ynew=f(xnew) 
 pl.plot(xnew,ynew,label=str(kind)) 
pl.legend(loc="lower right") 
pl.show()

結果：

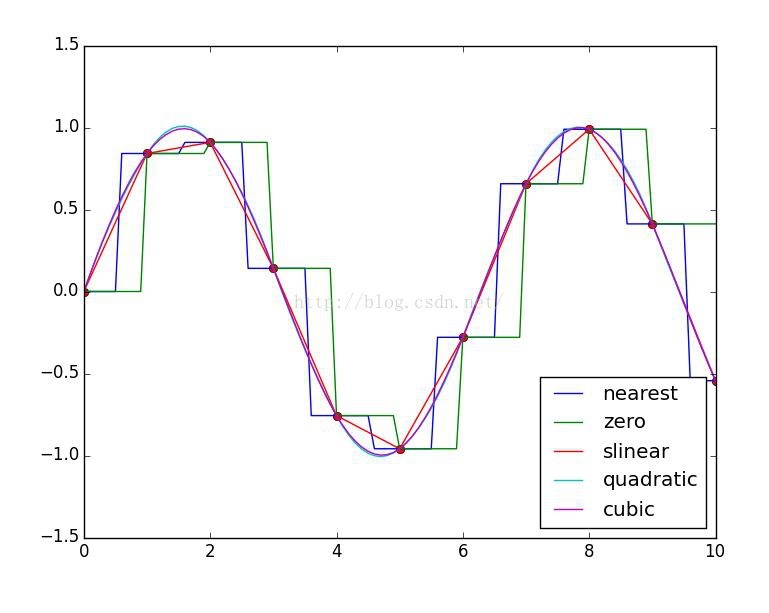
二次元補間

この方法は、2次元スプライン補間である1次元データ補間に似ています。

CODEでコードピースを表示し、私のコードピースから派生

# - *- coding: utf-8-*-""" 
2次元補間を示します。
""" 
import numpy as np 
from scipy import interpolate 
import pylab as pl 
import matplotlib as mpl 
 
def func(x, y):return(x+y)*np.exp(-5.0*(x**2+ y**2)) 
 
# X-Y軸は15に分割されます*15グリッド
y,x= np.mgrid[-1:1:15j,-1:1:15j] 
 
fvals =func(x,y) #各グリッドポイント15で関数値を計算します*15の値
print len(fvals[0]) 
 
# キュービックスプライン2次元補間
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic') 
 
# 100を計算する*100のグリッドでの補間
xnew = np.linspace(-1,1,100)#x 
ynew = np.linspace(-1,1,100)#y 
fnew =newfunc(xnew, ynew)#ちょうどy値100*100の値
 
# 図
# 補間前後の違いをより明確に比較するには、キーワードパラメータ補間を使用します='nearest' 
# imshowを閉じる()組み込みの補間操作。
pl.subplot(121) 
im1=pl.imshow(fvals, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")#pl.cm.jet 
# extent=[-1,1,-1,1]バツ,y範囲のお気に入りは
pl.colorbar(im1) 
 
pl.subplot(122) 
im2=pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower") 
pl.colorbar(im2) 
 
pl.show()

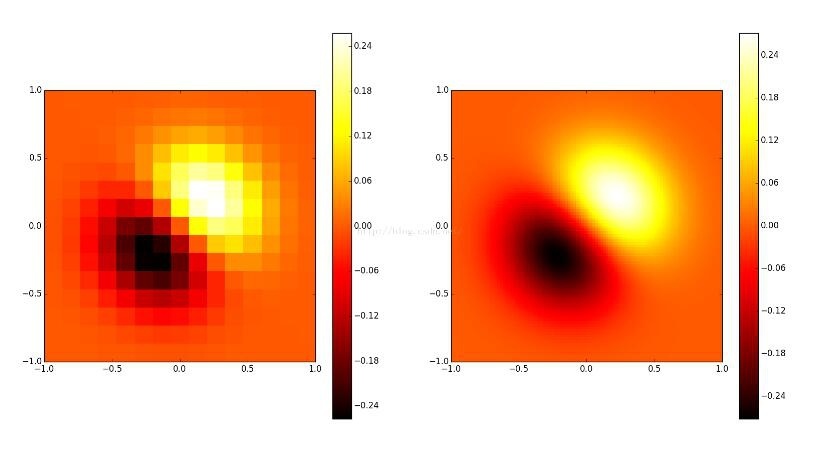
左の写真は元のデータで、右の写真は2次元補間の結果です。

2D補間の3D表示方式

CODEでコードピースを表示し、私のコードピースから派生

# - *- coding: utf-8-*-""" 
2次元補間を示します。
""" 
# - *- coding: utf-8-*-import numpy as np 
from mpl_toolkits.mplot3d import Axes3D 
import matplotlib as mpl 
from scipy import interpolate 
import matplotlib.cm as cm 
import matplotlib.pyplot as plt 
 
def func(x, y):return(x+y)*np.exp(-5.0*(x**2+ y**2)) 
 
# X-Y軸は20に分割されます*20グリッド
x = np.linspace(-1,1,20) 
y = np.linspace(-1,1,20) 
x, y = np.meshgrid(x, y)#20*20グリッドデータ
 
fvals =func(x,y) #各グリッドポイント15で関数値を計算します*15の値
 
fig = plt.figure(figsize=(9,6)) 
# Draw sub-graph1 
ax=plt.subplot(1,2,1,projection ='3d') 
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True) 
ax.set_xlabel('x') 
ax.set_ylabel('y') 
ax.set_zlabel('f(x, y)') 
plt.colorbar(surf, shrink=0.5, aspect=5)#ラベル
 
# 二次元補間
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')#newfuncは関数です
 
# 100を計算する*100のグリッドでの補間
xnew = np.linspace(-1,1,100)#x 
ynew = np.linspace(-1,1,100)#y 
fnew =newfunc(xnew, ynew)#ちょうどy値100*100npの値.shape(fnew) is 100*100 
xnew, ynew = np.meshgrid(xnew, ynew) 
ax2=plt.subplot(1,2,2,projection ='3d') 
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True) 
ax2.set_xlabel('xnew') 
ax2.set_ylabel('ynew') 
ax2.set_zlabel('fnew(x, y)') 
plt.colorbar(surf2, shrink=0.5, aspect=5)#ラベル
 
plt.show()

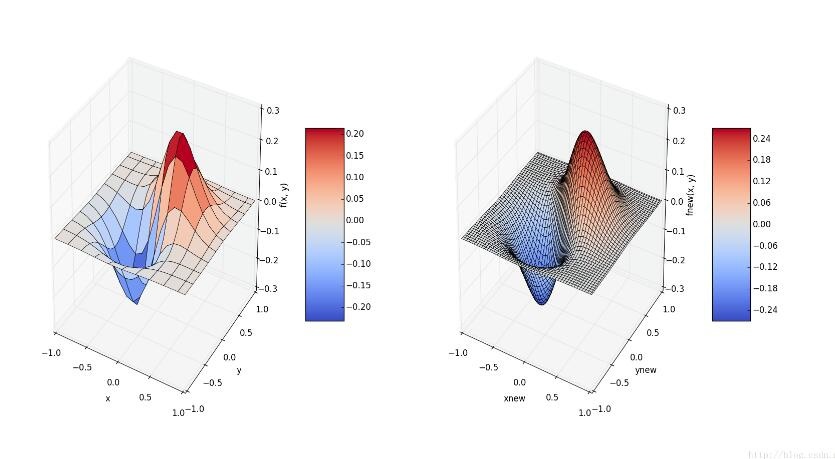
左側の2次元データセットの関数値は、サンプルが少ないために粗く表示されます。右の図は、2次元のサンプルデータに対して3次スプライン補間を行っており、フィッティングによりより多くのデータポイントのサンプル値が得られており、描画後の画像は明らかに滑らかになっています。

**補足知識：python **でのデータフレーム2次元ルックアップテーブル補間の実装方法

今日、風エネルギーを取り込むために風力タービンの出力を計算するときは、ブレードのスイープエリア内の風エネルギー、つまりCp係数の電力効率を下げる必要があります。Cpは次のように定義されます。つまり、実際に使用された風エネルギーと入力風エネルギーの比率です。

入力風エネルギーは、空気密度と風速の関数であり、直接計算できます。

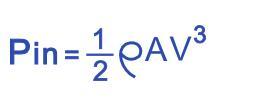
その場合、得られる実際の能力はピンとCpの積です。

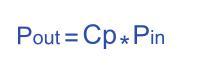
Cpは通常2次元のテーブルで、横軸はTSR（ブレードの先端速度と風速の比率）、縦軸はPITCH角度（ブレード角度）です。風力タービンの運転データには、風速、回転速度、ブレード角度の情報が含まれており、DataFrameに直接読み込むことにより、TSRとPAのCpに基づいてテーブルを検索し、補間してCpを取得する必要があります。 Scipy.interpolate.interp2dは、主に補間関数の作成とテーブルの検索に使用されます。また、補間関数をデータフレームで直接使用することはできません。ここでは、forループ分岐補間ルックアップテーブルを作成します。

from scipy.interpolate import interp2d
df_rotormap = pd.read_csv('filepath',header = None) #Cpテーブルを読む
x = np.array(df_rotormap.iloc[:,0].dropna()) #CpテーブルのX座標はTSRです
y = np.array(df_rotormap.iloc[:,1]) #CpテーブルのY座標はピッチ角です
z = np.array(df_rotormap.iloc[:,2:]) #Cpテーブル、y行x列の特定の値

rho =1.225 #kg/m3
s =(141/2)**2*np.pi #m2
df_cal['TSR']= df_cal['発電機速度（PDM1）']/148*141*np.pi/60/df_cal['風速']

func_new =interp2d(x,y,z,kind ='linear') #2次元テーブル補間関数を定義し、線形補間を選択します

cp_list =[]for i inrange(df_cal.shape[0]):
 cp =float(func_new(df_cal['TSR'][i],df_cal['No.1ブレード角度'][i])) #Xを入力してください,Y座標、補間によって計算された出力Cp
 cp_list.append(cp)

df_cal['cp']= cp_list #Cpをデータフレームに戻します

df_cal['air_power']=0.5*rho*s*df_cal['風速']**3*df_cal['cp']

上記のpython1次元2次元補間の例は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。