Python補間補間の例

ナンセンスなことはあまり言いませんが、みんなコードを見てください〜

import numpy as np
# scipyライブラリから補間に必要なメソッドをインポートしますinterpolate
from scipy import interpolate
# データの視覚化,スキャッタプロットを描く
import matplotlib.pyplot as plt

定義関数x：横リストy：縦リスト種類：補間法

f = interpolate.interp1d(x, y, kind=’cubic’)

補間方法：

最も近い：最も近い隣接補間

ゼロ：ステップ補間

slinear、linear：線形補間

二次、三次：2、3次Bスプライン曲線補間

# 新しい横長リストを定義する
x_new=list(np.arange(0,15,0.5))
y_new=list(f(x_new))
plt.plot(x,y,'r',label='original values')
plt.plot(x_new,y_new,'b',label='interpolated values')
plt.show()
plt.close()

補足知識：python scipyスプライン補間関数（補間のinterpld関数）

scipyスプライン補間

1、 スプライン補間は、可変スプラインを使用して一連のポイントを通る滑らかな曲線を作成する数学的な方法です。補間スプラインはいくつかの多項式で構成され、各多項式は2つの隣接するデータポイントによって決定されます。このように、任意の2つの隣接する多項式とその導関数（Qiの次数の導関数を除く）は接続ポイントにあります。それはどこでも継続しています。接続ポイントの滑らかさと連続性は、スプライン補間とピースワイズ多項式補間の主な違いです。

2、 Scipyでは、scipy.interpolateモジュールの下にあるinterpld関数を使用して、スプライン補間を実装できます。 SciPyのバージョン0.14.0のスプライン補間方法には、「線形」、「ゼロ」、「線形」、「二次」（2回）、「立方」（3回）、4、5などがあります。

3、 scipy複数スプライン補間の適用形式は次のとおりです。

import numpy as np, matplotlib.pyplot as plt
from scipy.interpolate import interpld #scipyのinterpolateモジュールにinterpld補間モジュールをインポートします
x= np.array([0,1,2,3,4,5,6,7])
y= np.array([3,4,3.5,2,1,1.5,1.25,0.9]) #離散点の分布
xx = np.linspace(x.min(), x.max(),100) #新しい補間間隔とポイント数
plt.scatter(x, y) #散布図
# for n in['linear','zero','slinear','quadratic','cubic',4,5]: #pythonscipyのさまざまな補間関数
f =interp1d(x, y,kind="cubic") #補間関数の形式を編集する
ynew=f(xx) #対応する補間関数を使用して新しい関数点を見つけます
plt.plot(xx,ynew,"g") #新しい機能点の出力画像
plt.show()

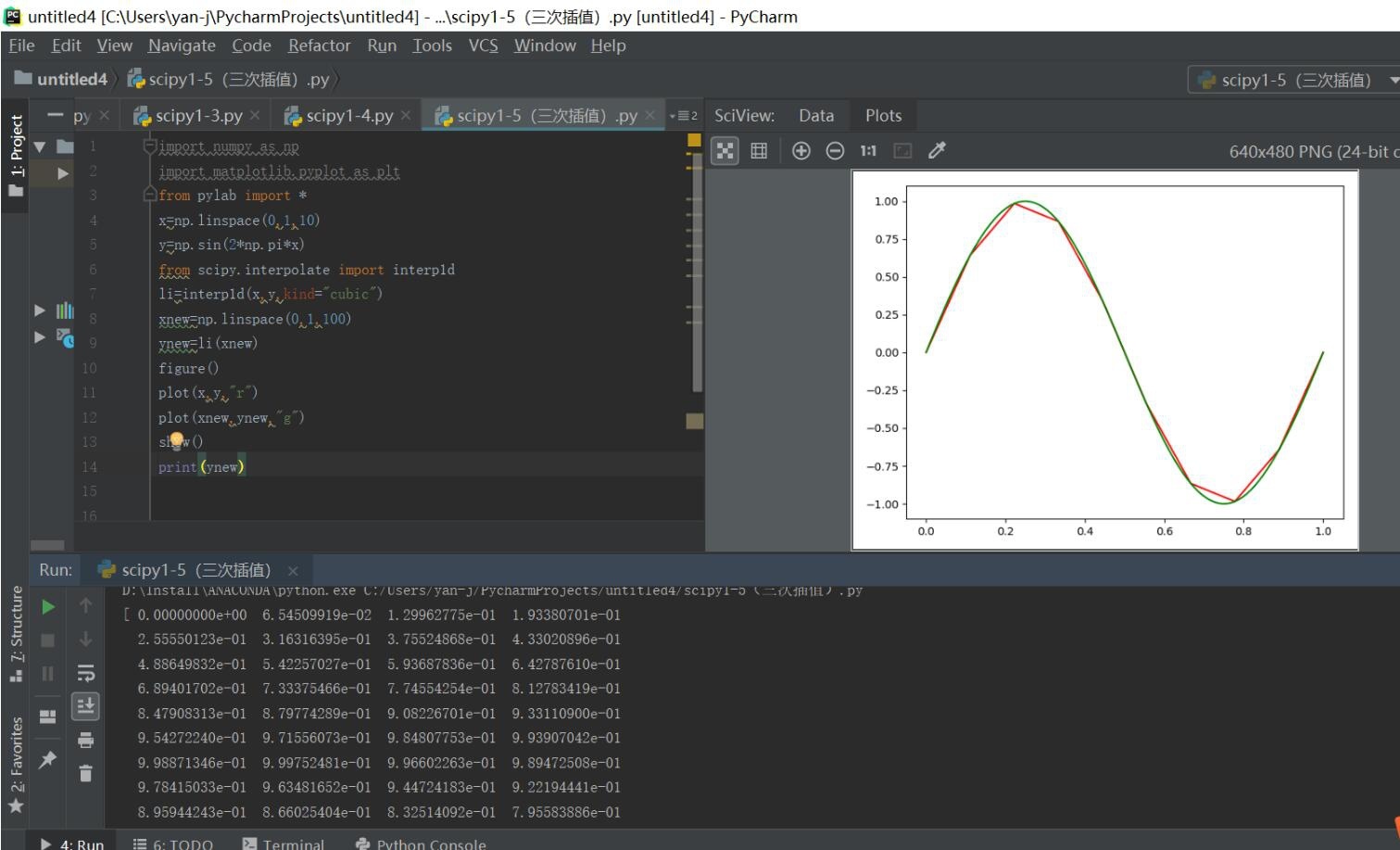
上記のpython補間補間の例は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。