Python classic algorithm

Algorithm implementation###

#0 GitHub

https://github.com/Coxhuang/Python-DataStructure

#1 surroundings##

Python3.7.3

#2 Start##

#2.1 Fibonacci Sequence###

GitHub

[ GitHub code](https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 %95/1.Fibonacci)

Problem Description
law
Code

Conventional implementation

def fib(max_val):
 a, b, n =0,1, max_val
 while n:print(a)
  a, b = b, a+b
  n -=1return None
fib(10)

Output

0112358132134

Builder

def fib(max_val):
 a, b, n =0,1, max_val
 while n:yield a
  a, b = b, a+b
  n -=1return None
for foo infib(10):print(foo)

Output

0112358132134

Recursion

def fib(n):if n <2:return n
 returnfib(n-1)+fib(n-2)for foo inrange(10):print(fib(foo))

Output

0112358132134

#2.2 Jump up the stairs###

GitHub

[ GitHub code](https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 %95/2.%E5%8F%B0%E9%98%B6%E9%97%AE%E9%A2%98)

Problem Description

**A frog can jump up to 1 step or 2 steps at a time (up to 2 steps). How many ways are there for the frog to jump to an n step? **

**If there is only one step, there is only one way to go; if there are two steps, there are two ways to go; if there are N steps, and finally jump to the Nth step, you can either jump directly from N-2 to two steps Steps, or jump one step from the N-1th step, so the number of methods for a step with N steps is equal to the number of methods to step N-2 steps plus the number of methods to step N-1 steps, that is, S(N )=S(N-1)+S(N-2), the initial term is S(1)=1, S(2)=2, which is similar to the Fibonacci sequence, but the initial term is different. **

Number of steps	Method
f(0)	0
f(1)	1
f(2)	2
f(3)	3
f(4)	5
f(5)	8
…	…

The logical law is consistent with the Fibonacci sequence

Code

def fib(max_val):
 a, b, n =0,1, max_val
 while n:
  a, b = b, a+b
  n -=1return b
n =3 #Number of steps
ret = n if n <=2elsefib(n)print(ret)

#2.3 Jumping steps (abnormal jump)

GitHub

[ GitHub code](https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 %95/3.%E5%8F%B0%E9%98%B6%E9%97%AE%E9%A2%98%28%E5%8F%98%E6%80%81%E8%B7%B3% 29)

Problem Description

**A frog can jump up to 1 step or 2 steps at a time...it can also jump to n steps. Find the total number of jumping methods the frog jumps on an n-level step. **

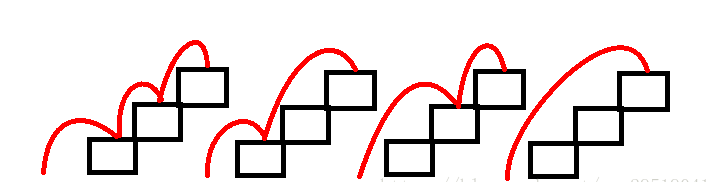
When jumping 1 step, f(1)=1;When jumping 2 steps, f(2)=f(1)+1=2;When jumping 3 steps, f(3)=f(2)+f(1)+1=4;When jumping 4 steps, f(4)=f(3)+f(2)+f(1)+1=8;f(n-1)=f(n-2)+...+f(2)+f(1)+1f(n)=f(n-1)+f(n-2)+...+f(2)+f(1)+1

Description:

3.1. Here f(n) represents the number of jumps where n steps have 1, 2, ... n steps.
3.2. When n = 1, there is only one jump method, f(1) = 1
3.3. When n = 2, there will be two ways to jump, one step 1 or 2, which returns to the problem (1), f(2) = f(2-1) + f(2-2)
3.4. When n = 3, there will be three ways to jump, 1st, 2nd, 3rd, then it is the first time to jump out of the first stage, and the rest: f(3-1); the first time to jump out of the second stage, the remaining f (3-2); The first time is 3 steps, then f(3-3) is left so the conclusion is:

f(3)=f(3-1)+f(3-2)+f(3-3)

3.5. When n = n, there will be n-step jumps, 1st order, 2nd order...nth order, and the conclusion is drawn:

f(n)=f(n-1)+f(n-2)+...+f(n-(n-1))+f(n-n)=>f(0)+f(1)+f(2)+f(3)+...+f(n-1)

3.6. The above is a conclusion, but for simplicity, we can continue to simplify:

f(n-1)=f(0)+f(1)+f(2)+f(3)+...+f((n-1)-1)=f(0)+f(1)+f(2)+f(3)+...+f(n-2)f(n)=f(0)+f(1)+f(2)+f(3)+...+f(n-2)+f(n-1)=f(n-1)+f(n-1)

3.7. Draw the final conclusion, when there are steps of 1, 2,...n steps in n steps, the total jumping method is:

|1,( n=0)|f(n)=|1,(n=1)||2*f(n-1),(n>=2)

Code

# Recursion-Method 1
def jump(n):while n<=2:return n
 returnjump(n-1)*2print(jump(5))

# Recursion-Method 2
def jump(n):while n<=2:return n
 return2**(n-1)print(jump(5))

#2.4 Rabbit breeding###

GitHub
Problem Description

**There is a pair of rabbits. A pair of rabbits will be born every month from the third month after birth, and a pair of rabbits will be born every month after the little rabbit grows to the third month. If the rabbits are not dead, ask the rabbits every month What is the total? **

Ideas

f(N): total number of rabbits in month N

f(Nbefore): rabbits born before the Nth month

f(Nnew): rabbit born in the Nth month

f(N) = f(Nbefore) + f(Nnew) = f(N-1) + f(Nnew)

When the (N+1)th month is reached: the rabbits born in the Nth month cannot breed yet, and all the rabbits born before the Nth month can breed

f(N+1) = f(Nnew) + f(Nbefore)2 = f(Nnew) + 2f(N-1)

by:f(N)=f(N-1)+f(Nnew)f(N+1)=f(Nnew)+2*f(N-1)

Get:f(N+1)=f(N)+f(N-1)

Code

def fib(max_val):
 a, b, n =1,2, max_val
 while n:
  a, b = b, a+b
  n -=1return b
n =5 #Month N
ret = n if n <=2elsefib(n)print(ret)

#2.5 List to heavy###

No time and space complexity limit

def func(tar):
 tar_copy =[]for foo in tar:if foo not in tar_copy:
   tar_copy.append(foo)return tar_copy
ret =func([1,2,2,2,2,3,4,5,6,7,8,9,8,1,2,3,4])print(ret)

time complexity

O(n)

Space complexity

O(n)

Ordered list + time complexity O(n) + space complexity O(1)

Means that there can only be one for loop + can only operate on the original table

def func(tar):for i,num inenumerate(tar):try: # tar[i+1]To the last one will throw an exception
   while num == tar[i+1]:
    tar.pop(i+1)
  except:breakreturn tar
ret =func([1,1,1,2,2,2,2,3,3,4,4,5,6,7,8,8,9,9,9])print(ret)

To be continued##

Python list/dictionary operation time complexity
https://blog.csdn.net/Coxhuang/article/details/90313828