Python implements ten classic sorting algorithms#

summary:

Operation mode, copy the last code out and run python sort.py directly;
There is not much to deal with the robustness in the code, and students who use it directly must check;
For Hill sorting, the choice of gap is very important and needs to be changed according to the actual situation;
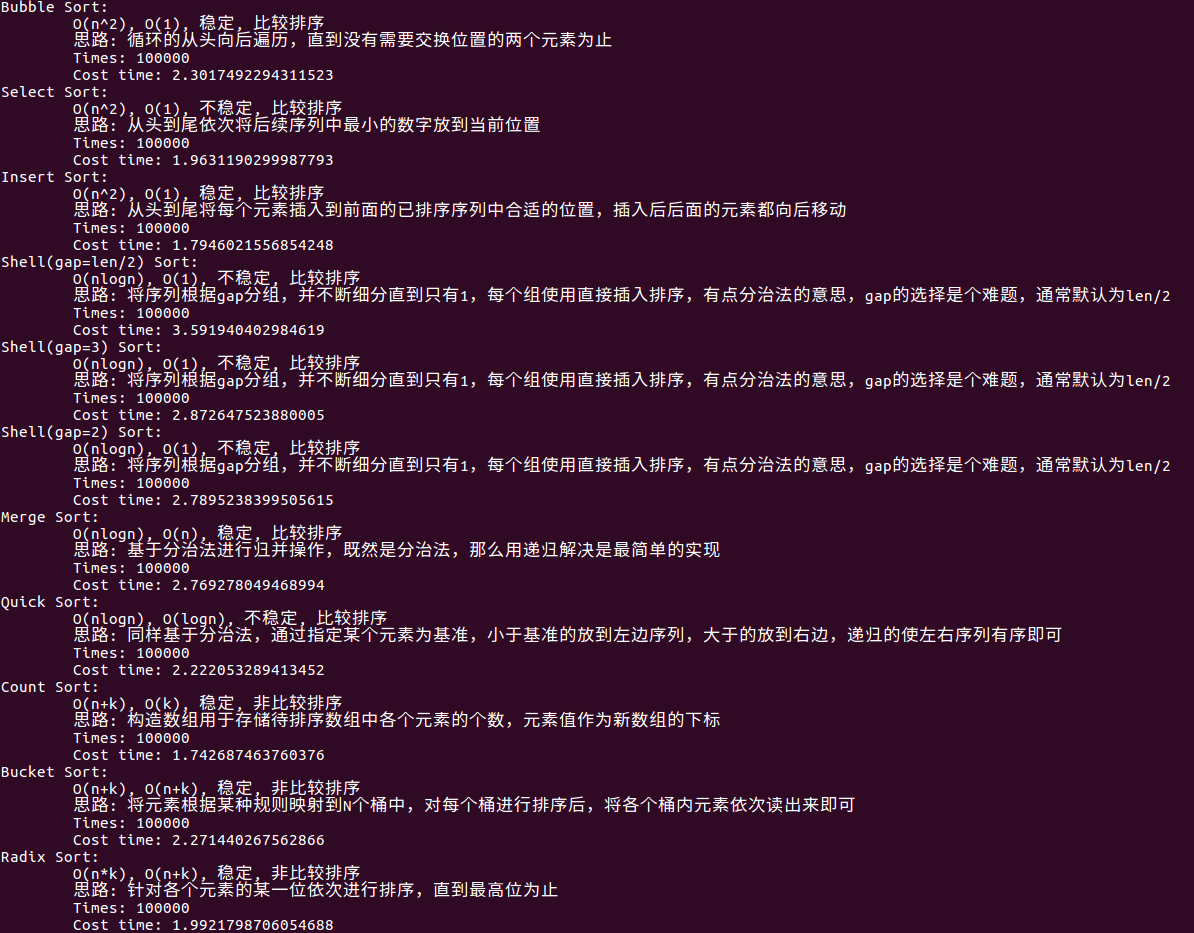
In my test, because the array to be sorted is very small, the length is only 10, and the maximum value is 10, the counting sort is the fastest, which is often not the case in actual situations;
Heap sort did not have time to implement, yes, it is lazy;
The key is to understand the idea of the algorithm. As for the realization, it is only to implement the idea in a reasonable way;
I recommend that everyone go to the link above to see the animated picture, it is indeed better to understand, but it is also good to read the code, right;
Divide and conquer is used a lot. In fact, I don’t know what the mathematical principle behind it is, and why divide and conquer can reduce time complexity. Some students told me in the trouble comment section, thank you;

Running diagram##

Since the array is small and the range is between 1 and 10, this is actually more friendly to the non-comparative algorithm of counting sorting, because there is not much space pressure, so counting sorting speed is easy to understand, and the reason for choosing , Insertion is faster than Hill merge, mainly because the size of the problem itself is too small, and my implementation of divide and conquer is based on recursion, so I can't see the advantages of divide and conquer, in fact, if you sort a very large array , This difference will be reflected;

Complete code##

As you can see, the entire code does not include the test code and there are only 170 lines in total. This also includes blank lines and function names, etc., so the algorithm implementation itself is very simple, and everyone should pay attention to the idea;

import sys,random,time

def bubble(list_):
 running = True
 while running:
  have_change = False
  for i inrange(len(list_)-1):if list_[i]>list_[i+1]:
    list_[i],list_[i+1]= list_[i+1],list_[i]
    have_change = True
  if not have_change:breakreturn list_

def select(list_):for i inrange(len(list_)-1):
  min_idx = i
  for j inrange(i,len(list_)):if list_[min_idx]>list_[j]:
    min_idx = j
  list_[i],list_[min_idx]= list_[min_idx],list_[i]return list_

def insert(list_):for i inrange(1,len(list_)):
  idx = i
  for j inrange(i):if list_[j]>list_[idx]:
    idx = j
    breakif idx != i:
   tmp = list_[i]
   list_[idx+1:i+1]= list_[idx:i]
   list_[idx]= tmp
 return list_

def shell(list_,gap=None):'''
 The choice of gap has a great impact on the result, which is a difficult problem. Hill recommends len./2
 This gap is actually a gap, that is, how many elements are separated by one group of elements
 For example for[1,2,3,4,5,6,7,8,9,10]
 When gap is len/When 2 is 5, the elements in each group are composed of 5 elements apart, that is, 1 and 6.,2 and 7,3 and 8 etc.
    '''
 len_ =len(list_)
 gap =int(len_/2)if not gap else gap
 while gap >=1:for i inrange(gap):
   list_[i:len_:gap]=insert(list_[i:len_:gap])
  gap =int(gap/2)return list_

def merge(list_):'''
 Recursive implementation of merge sort
 Idea: Divide the data to two groups, and then sort the two groups into a group of 4 elements.
 Until the entire sequence is traced back, it is actually composed of two ordered subsequences, a typical recursive problem
    '''
 iflen(list_)<=1:return list_
 iflen(list_)==2:return list_ if list_[0]<=list_[1]else list_[::-1]
 len_ =len(list_)
 left =merge(list_[:int(len_/2)])
 right =merge(list_[int(len_/2):])
 tmp =[]
 left_idx,right_idx =0,0whilelen(tmp)<len(list_):if left[left_idx]<=right[right_idx]:
   tmp.append(left[left_idx])
   left_idx+=1if left_idx==len(left):
    tmp += right[right_idx:]breakelse:
   tmp.append(right[right_idx])
   right_idx+=1if right_idx==len(right):
    tmp += left[left_idx:]breakreturn tmp

def quick(list_):'''
 Quick sort: based on the divide and conquer method, select an element as the benchmark, and place the remaining elements on the left and right sides of the benchmark, recursively this process
    '''
 iflen(list_)<=1:return list_
 iflen(list_)==2:return list_ if list_[0]<=list_[1]else list_[::-1]
 base_idx =int(len(list_)/2)
 base = list_[base_idx]
 left =[]
 right =[]for i inrange(len(list_)):if i != base_idx:if list_[i]<= base:
    left.append(list_[i])else:
    right.append(list_[i])returnquick(left)+[base]+quick(right)

def count(list_):'''
 Requires elements to be integer
    '''
 min_,max_ = list_[0],list_[0]for i inrange(1,len(list_)):if list_[i]<min_:
   min_ = list_[i]if list_[i]>max_:
   max_ = list_[i]
 count_list =[0]*(max_-min_+1)for item in list_:
  count_list[item-min_]+=1

 list_ =[]for i inrange(len(count_list)):for j inrange(count_list[i]):
   list_.append(i+min_)return list_

def heap(list_):'''

    '''
 pass

def bucket(list_):'''
 Each bucket uses selective sorting, and the bucketing method is the maximum value divided by 5, which is divided into 5 buckets
 The speed of bucket sorting depends on how the buckets are sorted
    '''
 bucket =[[],[],[],[],[]] #Note that the length is 5
 max_ = list_[0]for item in list_[1:]:if item > max_:
   max_ = item
 gap = max_/5 #The length of the corresponding bucket
 for item in list_:
  bucket[int((item-1)/gap)].append(item)for i inrange(len(bucket)):
  bucket[i]=select(bucket[i])
 list_ =[]for item in bucket:
  list_ += item
 return list_

def radix(list_):'''
 Cardinality sorting: sort the different digits of the value, for example, start with the ones digit, then tens, hundreds, and so on;
 Note that the code here assumes that the values to be sorted are all integers
    '''
 max_ = list_[0]for item in list_[1:]:if item > max_:
   max_ = item
 max_radix =len(str(max_))
 radix_list =[[],[],[],[],[],[],[],[],[],[]] #Corresponds to 9 possible numbers on each digit
 cur_radix =0while cur_radix<max_radix:
  base =10**cur_radix
  for item in list_:
   radix_list[int(item/base)%10].append(item)
  list_ =[]for item in radix_list:
   list_ += item

  radix_list =[[],[],[],[],[],[],[],[],[]] #Corresponds to 9 possible numbers on each digit
  cur_radix +=1return list_

def test(name,sort_func,times,info,idea,*param):
 list_ =[1,2,3,4,5,6,7,8,9,10]print(name+' Sort:')print('\t'+info)print('\t'+idea)print('\tTimes: '+str(times))
 start_time = time.time()for i inrange(times):
  random.shuffle(list_)
  # print('\tInput: '+str(list_))
  list_ =sort_func(list_)iflen(param)<=0elsesort_func(list_,param[0])
  # print('\tOutput: '+str(list_))
 # print('\t'+str(list_))print('\tCost time: '+str(time.time()-start_time))if __name__ =="__main__":test('Bubble',bubble,100000,'O(n^2), O(1),stable,Comparison sort','Ideas:Loop back and forth from the beginning until there are no two elements that need to swap positions')test('Select',select,100000,'O(n^2), O(1),Unstable,Comparison sort','Ideas:Put the smallest number in the subsequent sequence to the current position from beginning to end')test('Insert',insert,100000,'O(n^2), O(1),stable,Comparison sort','Ideas:From beginning to end, insert each element to the appropriate position in the previous sorted sequence, and all subsequent elements move backward after insertion')test('Shell(gap=len/2)',shell,100000,'O(nlogn), O(1),Unstable,Comparison sort','Ideas:The sequence is grouped according to the gap and continuously subdivided until there is only 1. Each group uses direct insertion sort, which means a bit of divide and conquer. The choice of gap is a difficult problem, and the default is len/2')test('Shell(gap=3)',shell,100000,'O(nlogn), O(1),Unstable,Comparison sort','Ideas:The sequence is grouped according to the gap and continuously subdivided until there is only 1. Each group uses direct insertion sort, which means a bit of divide and conquer. The choice of gap is a difficult problem, and the default is len/2',3)test('Shell(gap=2)',shell,100000,'O(nlogn), O(1),Unstable,Comparison sort','Ideas:The sequence is grouped according to the gap and continuously subdivided until there is only 1. Each group uses direct insertion sort, which means a bit of divide and conquer. The choice of gap is a difficult problem, and the default is len/2',2)test('Merge',merge,100000,'O(nlogn), O(n),stable,Comparison sort','Ideas:Merge operation based on divide-and-conquer method. Since it is divide-and-conquer method, recursive solution is the simplest implementation')test('Quick',quick,100000,'O(nlogn), O(logn),Unstable,Comparison sort','Ideas:Also based on the divide-and-conquer method, by specifying a certain element as the benchmark, the ones smaller than the benchmark are placed in the left sequence, those larger than the benchmark are placed on the right, and the left and right sequences are recursively ordered')
 # test('Heap',heap,100000,'O(nlogn), O(1),Unstable,Comparison sort','Ideas:Use the nature of heap to construct a complete binary tree')test('Count',count,100000,'O(n+k), O(k),stable,Non-comparative sort','Ideas:Construct an array to store the number of elements in the array to be sorted, and the element value is used as the subscript of the new array')test('Bucket',bucket,100000,'O(n+k), O(n+k),stable,Non-comparative sort','Ideas:Map elements to N buckets according to a certain rule, and after sorting each bucket, read the elements in each bucket in turn.')test('Radix',radix,100000,'O(n*k), O(n+k),stable,Non-comparative sort','Ideas:Sort each element in sequence until the highest position')

 # print(heap([4,6,8,3,5,10,9,2,1,7]))