python implements the gradient method python the fastest descent method

Suppose we already know the principle of the gradient method-the steepest descent method.

Now give an example:

If you solve directly manually:

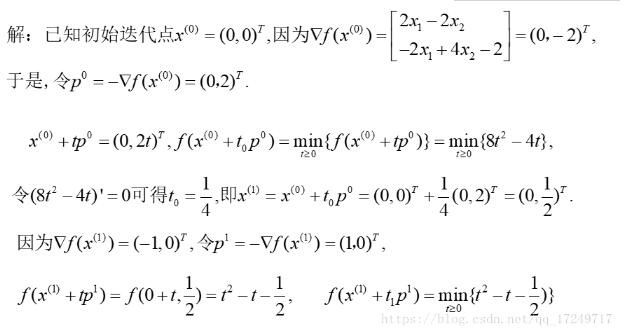
Now give the Python solution process:

import numpy as np
from sympy import*import math
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist

# Definition symbol
x1, x2, t =symbols('x1, x2, t')

def func():
 # Customize a function
 returnpow(x1,2)+2*pow(x2,2)-2* x1 * x2 -2* x2

def grad(data):
 # Find the gradient vector,data=[data1, data2]
 f =func()
 grad_vec =[diff(f, x1),diff(f, x2)] #Find the partial derivative,Gradient vector
 grad =[]for item in grad_vec:
 grad.append(item.subs(x1, data[0]).subs(x2, data[1]))return grad

def grad_len(grad):
 # Modulus length of gradient vector
 vec_len = math.sqrt(pow(grad[0],2)+pow(grad[1],2))return vec_len

def zhudian(f):
 # Find min(t)Stagnation point
 t_diff =diff(f)
 t_min =solve(t_diff)return t_min

def main(X0, theta):
 f =func()
 grad_vec =grad(X0)
 grad_length =grad_len(grad_vec) #Modulus length of gradient vector
 k =0
 data_x =[0]
 data_y =[0]while grad_length   theta: #Termination condition of iteration
 k +=1
 p =-np.array(grad_vec)
 # Iteration
 X = np.array(X0)+ t*p
 t_func = f.subs(x1, X[0]).subs(x2, X[1])
 t_min =zhudian(t_func)
 X0 = np.array(X0)+ t_min*p
 grad_vec =grad(X0)
 grad_length =grad_len(grad_vec)print('grad_length', grad_length)print('coordinate', X0[0], X0[1])
 data_x.append(X0[0])
 data_y.append(X0[1])print(k)

 # Drawing
 fig = plt.figure()
 ax = axisartist.Subplot(fig,111)
 fig.add_axes(ax)
 ax.axis["bottom"].set_axisline_style("-| ", size=1.5)
 ax.axis["left"].set_axisline_style("- ", size=1.5)
 ax.axis["top"].set_visible(False)
 ax.axis["right"].set_visible(False)
 plt.title(r'$Gradient \ method - steepest \ descent \ method$')
 plt.plot(data_x, data_y, label=r'$f(x_1,x_2)=x_1^2+2 \cdot x_2^2-2 \cdot x_1 \cdot x_2-2 \cdot x_2$')
 plt.legend()
 plt.scatter(1,1, marker=(5,1), c=5, s=1000)
 plt.grid()
 plt.xlabel(r'$x_1$', fontsize=20)
 plt.ylabel(r'$x_2$', fontsize=20)
 plt.show()if __name__ =='__main__':
 # Given initial iteration point and threshold
 main([0,0],0.00001)

The final result is shown below:

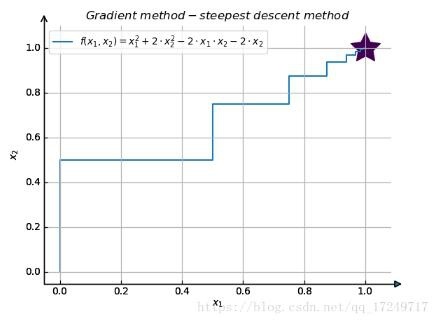
The above is the whole content of this article, I hope it will be helpful to everyone's study.