派生物を計算してプロットするpythonの例

私はナンセンスな話をやめます、ただコードに行ってください！

import math
import numpy as np
import matplotlib.pyplot as plt
from sympy import* #微分積分などの科学的計算に使用されます
 
 
def dif(left,right,step):#派生的な左右の間隔と間隔
 x,y =symbols('x y')#xy変数を導入する
 expr =pow(x,5)#計算式
 x_value =[] #save x value
 y_value =[] #save x f(x) value
 y_value_dif =[] #save x f(x)_dot value
 y_value_dif2 =[] #save x f(x)_dot2 value
 y_value_dif3 =[] #save x f(x)_dot3 value
 y_value_dif4 =[] #save x f(x)_dot4 value
 # print(expand(exp(I*x), complex=True))#複雑な指数を実数部と虚数部の形に拡張します
 expr_dif =diff(expr,x,1)
 expr_dif2 =diff(expr,x,2)
 expr_dif3 =diff(expr,x,3)
 expr_dif4 =diff(expr,x,4)for i in np.arange(left,right,step):
 x_value.append(i)
 y_value.append(expr.subs('x',i))#iの値を式に代入します
 y_value_dif.append(expr_dif.subs('x',i))#iの値を微分式に代入します
 y_value_dif2.append(expr_dif2.subs('x',i))#iの値を2次微分式に代入します
 y_value_dif3.append(expr_dif3.subs('x',i))#iの値を3次微分式に代入します
 y_value_dif4.append(expr_dif4.subs('x',i))#iの値を4次微分式に代入します
 draw_plot_set()#描画フォーマットを設定する
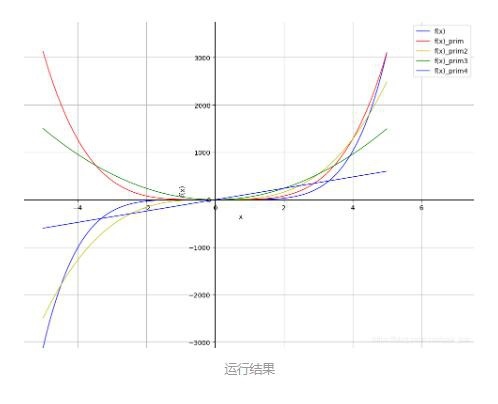
 plt.plot(x_value,y_value,"b-",linewidth=1,label='f(x)='+str(expr)) #図
 plt.plot(x_value,y_value_dif,"r-",linewidth=1,label='f(x)_prim') #図
 plt.plot(x_value,y_value_dif2,"y-",linewidth=1,label='f(x)_prim2') #図
 plt.plot(x_value,y_value_dif3,"g-",linewidth=1,label='f(x)_prim3') #図
 plt.plot(x_value,y_value_dif4,"b-",linewidth=1,label='f(x)_prim4') #図
 
 plt.legend()#凡例を表示
 plt.show()#画像を表示
 
 
def draw_plot_set():#描画フォーマットを設定する
 plt.figure()
 ax = plt.gca()
 # 軸位置を変更する
 ax.spines['right'].set_color('none')#元の軸を削除する
 ax.spines['top'].set_color('none')#元の軸を削除する
 ax.xaxis.set_ticks_position('bottom')#0に軸を追加
 ax.spines['bottom'].set_position(('data',0))
 ax.yaxis.set_ticks_position('left')#0に軸を追加
 ax.spines['left'].set_position(('data',0))
 # 座標名を設定する
 plt.ylabel('f(x)')
 plt.xlabel('x')
 
 plt.grid(True)#オープングリッド
 
 
 
 
if __name__ =='__main__':dif(-5,5,0.01)

補足拡張：pythonはsympyライブラリを使用して関数を導出し、numpyライブラリはプログラムを使用して導出結果を計算します

pythonデータ処理の過程で、私たちはしばしばそのような状況に遭遇します。関数式の部分導関数を取得し、導関数式に特定の値を代入する必要があります。

pythonで関数を導出するために通常使用できる関数は、sympyライブラリのdiff（）関数です。

しかし、彼が通常見つける派生物は、単なる象徴的な表現です。データに直接使用することはできません。

次の例：

import sympy as sp
import numpy as np
x,y = sp.symbols('x y')
z = sp.sin(2*sp.pi*x+2*y/5)
zx = sp.diff(z,x)
zy = sp.diff(z,y)print(zx)print(zy)

出力は次のとおりです。

2* pi*cos(2*pi*x +2*y/5)2*cos(2*pi*x +2*y/5)/5

**では、この問題をどのように解決するのでしょうか？ ****

evalf（）関数を使用してxとyにそれぞれ値を割り当て、floatを使用して型変換を行った後、numpyを数値計算に使用できます。

次の例：

import sympy as sp
import numpy as np
x,y = sp.symbols('x y')
z = sp.sin(2*sp.pi*x+2*y/5)
zx = sp.diff(z,x)
zy = sp.diff(z,y)
x1 =10
y1 =5
z_x1 =float(zx.evalf(subs={x:x1,y:y1}))
z_y1 =float(zy.evalf(subs={x:x1,y:y1}))print(z_x1)print(z_y1)

出力結果：

-2.61472768902227-0.16645873461885696

xまたはyが単一の値でない場合はどうなりますか？配列です。

ループを使用して完了することができます。

次の例：

import sympy as sp
import numpy as np
x,y = sp.symbols('x y')
z = sp.sin(2*sp.pi*x+2*y/5)
zx = sp.diff(z,x)
zy = sp.diff(z,y)
x_array = np.linspace(-5,5,10)
y_array = np.linspace(-5,5,10)
temp_x =[]#まず、xの部分導関数を格納するための空のリストを定義します
temp_y =[]#まず、y個の部分導関数を格納するための空のリストを定義します
for i inrange(10):
 z_x =float(zx.evalf(subs={x:x_array[i],y:y_array[i]}))
 temp_x.append(z_x)#計算された部分導関数を1つずつリストに追加します
 z_y =float(zy.evalf(subs={x:x_array[i],y:y_array[i]}))
 temp_y.append(z_y)
zx_array = np.array(temp_x)#リストを配列に変換する
zy_array = np.array(temp_y)print(zx_array)print(zy_array)

出力は次のとおりです。

[-2.614727694.111638646.029462890.89585862-5.2854481-5.28544810.895858626.029462894.11163864-2.61472769][-0.166458730.261755050.383847530.05703213-0.33648208-0.336482080.057032130.383847530.26175505-0.16645873]

このようにして、sympyによって得られた導出結果が実現され、numpyライブラリで数値計算が実行されます。

上記のpython計算の派生物と描画の例は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。