pythonを使用して段階的な回帰を実現します
段階的回帰の基本的な考え方は、変数を1つずつモデルに導入することです。各説明変数が導入された後、Fテストが実行され、選択された説明変数が1つずつテストされます。最初に導入された説明変数が後続の説明変数によるものである場合イントロダクションが重要でなくなると、削除されます。新しい変数が導入される前に、重要な変数のみが回帰方程式に含まれるようにするため。これは、重要な説明変数が回帰方程式に選択されなくなり、重要でない説明変数が回帰方程式から削除されなくなるまでの反復プロセスです。説明変数の最終セットが最適であることを確認します。
この例の段階的回帰は変更されています。tテストは、導入された変数に対しては実行されず、変数が導入および除外されたかどうかのみが実行されます。「二重テスト」段階的回帰は、段階的回帰と呼ばれます。リンクの例:(元のリンクの有効期限が切れています)、4つの独立変数、1つの従属変数。以下では数学の推論は行わず、計算プロセスについて説明します。数学理論を理解していない人は、「現代の中長期の水文予測の方法と応用」を参照してください。TangChengyou、Guan Xuewen、Zhang Shiming、論文「ダム予測における段階的回帰モデル」 「王暁平等」への応募。
段階的回帰計算の手順:
-
ゼロステップ増強行列を計算します。ゼロステップの拡張マトリックスは、予測子と予測されたオブジェクトの間の相関係数で構成されています。
-
導入要因。拡張行列に基づいて、各因子の分散寄与を計算し、方程式に入力されていない因子の中から最大の分散寄与に対応する因子を選択し、因子の分散比を計算し、F分布表をチェックして、因子が方程式に導入されているかどうかを判断します。
-
除去係数。この時点で方程式に導入された因子の分散寄与を計算し、分散寄与が最小の因子を選択し、因子の分散比を計算し、F分布表をチェックして、因子が方程式から除外されているかどうかを判断します。
-
マトリックス変換。ゼロステップ行列は、導入された方程式の因子番号に従って変換され、変換された行列は、因子が導入できなくなり、因子が除去できなくなるまで、因子の導入と除去のステップに再びさらされ、段階的回帰分析の計算が終了します。
**a。次のコードは、データを読み取り、相関係数を計算し、0番目のステップの拡張行列を生成するためのサブルーチンを実装します。 ****
注:pandasライブラリは、csvデータ構造をDataFrame構造として読み取ります。これは、計算のためにnumpyの(n次元配列、ndarray)配列に変換されます。
import numpy as np
import pandas as pd
# 読み取ったデータ
# パンダを使用してcsvを読み取ります。読み取られたデータはDataFrameオブジェクトです
data = pd.read_csv('sn.csv')
# DataFrameオブジェクトを配列に変換します,配列の最後の列は予測オブジェクトです
data= data.values.copy()
# print(data)
# 回帰係数、パラメーターを計算する
def get_regre_coef(X,Y):
S_xy=0
S_xx=0
S_yy=0
# 予測係数と予測オブジェクトの平均値を計算します
X_mean = np.mean(X)
Y_mean = np.mean(Y)for i inrange(len(X)):
S_xy +=(X[i]- X_mean)*(Y[i]- Y_mean)
S_xx +=pow(X[i]- X_mean,2)
S_yy +=pow(Y[i]- Y_mean,2)return S_xy/pow(S_xx*S_yy,0.5)
# 元の拡張マトリックスを作成します
def get_original_matrix():
# 相関係数を格納する配列を作成します,data.数行の形(寸法)いくつかの列、結果はタプルで表されます
# print(data.shape[1])
col=data.shape[1]
# print(col)
r=np.ones((col,col))#np.onesパラメータはタプルです(tuple)
# print(np.ones((col,col)))
# for row in data.T:#配列の反復を使用すると、行を反復し、転置された配列を反復し、結果を転置することは、各列を反復することと同等です。
# print(row.T)for i inrange(col):for j inrange(col):
r[i,j]=get_regre_coef(data[:,i],data[:,j])return r
**b。2番目の部分は、主に許容誤差の寄与と分散比を計算することです。 ****
def get_vari_contri(r):
col = data.shape[1]
# 分散寄与値を格納するためのマトリックスを作成します
v=np.ones((1,col-1))
# print(v)for i inrange(col-1):
# v[0,i]=pow(r[i,col-1],2)/r[i,i]
v[0, i]=pow(r[i, col -1],2)/ r[i, i]return v
# 因子が方程式に入るかどうかを選択し、
# パラメータの説明:rは拡張行列、vは分散寄与値、kは最大の分散寄与値を持つ係数の添え字です。,pは現在方程式に入っている因子の数です
def select_factor(r,v,k,p):
row=data.shape[0]#サンプルサイズ
col=data.shape[1]-1#予測子の数
# 分散比を計算する
f=(row-p-2)*v[0,k-1]/(r[col,col]-v[0,k-1])
# print(calc_vari_contri(r))return f
c。3番目の部分は、定義された関数を呼び出して、分散寄与値を計算します
# ゼロステップ増強行列を計算する
r=get_original_matrix()
# print(r)
# 分散寄与値を計算する
v=get_vari_contri(r)print(v)
# 分散比を計算する
計算結果:
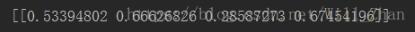
分散への最大の寄与を判断するサブルーチンはありません。他の計算では、変数の特定の物理的意味も必要であるため、計算によって変数の選択を簡単に決定することはできません。ここでは、4番目の変数が二乗チェックに最も寄与することがわかります。
# # 分散比を計算する
# print(data.shape[0])
f=select_factor(r,v,4,0)print(f)
####### 出力##########
22.79852020138227
4番目の予測子(コードに貼り付けられている)の分散比を計算し、比較のためにF分布テーブル3.280、22.8 3.28を確認し、4番目の予測子を導入します。 (椅子を除く計算は最初の3回は実行されません)
**d。4番目の部分は、マトリックス変換を実行します。 ****
# 段階的回帰分析と計算
# マトリックス変換式により、拡張マトリックスの各部分の要素値を計算します。
def convert_matrix(r,k):
col=data.shape[1]
k=k-1#行0からカウントを開始します
# 行kの要素リストは、列kの要素に属していません。
r1 = np.ones((col, col)) # np.onesパラメータはタプルです(tuple)for i inrange(col):for j inrange(col):if(i==k and j!=k):
r1[i,j]=r[k,j]/r[k,k]elif(i!=k and j!=k):
r1[i,j]=r[i,j]-r[i,k]*r[k,j]/r[k,k]elif(i!= k and j== k):
r1[i,j]=-r[i,k]/r[k,k]else:
r1[i,j]=1/r[k,k]return r1
e。マトリックス変換を実行した後、上記の手順を繰り返して、要因を導入および削除します
各因子の分散寄与を再度計算します

方程式に導入されていない最初の3つの分散係数がソートされ、最初の係数の分散寄与が取得されます。最初の予測子のFテスト値が計算され、最初の予測子が臨界値より大きい場合は方程式に導入されます。
# マトリックス変換、最初のステップのマトリックスを計算します
r=convert_matrix(r,4)
# print(r)
# 最初のステップの分散寄与値を計算します
v=get_vari_contri(r)
# print(v)
f=select_factor(r,v,1,1)print(f)
######### 出力#####
108.22390933074443
マトリックス変換を実行し、分散の寄与を計算します
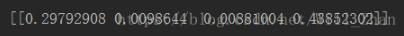
式の因子2と3が導入されておらず、より大きな分散に寄与する因子2が因子2であることがわかります。因子2のfテスト値は5.026 3.28と計算されるため、予測因子2が導入されます。
f=select_factor(r,v,2,2)print(f)
########## 出力#########
5.025864648951804
マトリックス変換を続行し、分散の寄与を計算します
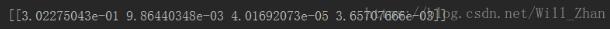
このステップでは、除去係数を考慮する必要があります。分散の寄与がある場合、係数4は、方程式に導入された係数の中で最小の分散の寄与を持っていることがわかります。係数3のインポートされたfテスト値は0.0183として計算されます。
ファクター4のfテスト値は1.863で3.28未満です(F分布表を確認してください)。ファクター3は導入できないため、ファクター4を削除する必要があります。現時点では、式に導入されるファクターの数は2です。
# 要因を除外するかどうかを選択し、
# パラメータの説明:rは拡張行列、vは分散寄与値、kは最大の分散寄与値を持つ係数の添え字です。,tは現在方程式に入っている因子の数です
def delete_factor(r,v,k,t):
row = data.shape[0] #サンプルサイズ
col = data.shape[1]-1 #予測子の数
# 分散比を計算する
f =(row - t -1)* v[0, k -1]/ r[col, col]
# print(calc_vari_contri(r))return f
# ファクター3インポートテスト値0.018233473487350636
f=select_factor(r,v,3,3)print(f)
# ファクター4除去試験値1.863262422188088
f=delete_factor(r,v,4,3)print(f)
ここでマトリックスを変換し、分散の寄与を計算します

、導入された因子(因子1および2)は、因子1の分散への寄与が最小であり、因子分散の導入への寄与が最大は因子4です。インポートされたfテスト値を計算し、2つのfテスト値を削除します。
# ファクター4インポートされたテスト値1.8632624221880876、3未満.28導入できません
f=select_factor(r,v,4,2)print(f)
# ファクター1拒否テスト値146.52265486251397,3より大きい.28は削除できません
f=delete_factor(r,v,1,2)print(f)
変数を削除または導入することはできず、この時点で段階的回帰の計算は停止されます。方程式に導入された要因は、前のブログで書かれた重回帰の助けを借りて、予測子1と予測子2です。多変量回帰は、方程式に入力された予測子と予測オブジェクトに対して実行されます。重回帰の予測結果を一定項として出力し、第1因子の予測係数、第2因子の予測係数を出力します。
# ファクター1とファクター2は方程式を入力します
# 方程式に入力された予測子に対して重回帰を実行します
# regs=LinearRegression()
X=data[:,0:2]
Y=data[:,4]
X=np.mat(np.c_[np.ones(X.shape[0]),X])#係数行列に定数係数を追加します
Y=np.mat(Y)#配列を行列に変換する
# print(X)
B=np.linalg.inv(X.T*X)*(X.T)*(Y.T)print(B.T)#出力係数,最初の項は定数項で、他の項は回帰係数です
### 出力##
#[[52.577348881.468305740.66225049]]
pythonを使用して段階的な回帰を実現する上記の記事は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。
Recommended Posts