Pythonデータサイエンス：線形回帰

以前に導入された変数の分析：

①相関分析：連続変数と連続変数の関係。

②** 2サンプルtテスト**：二分されたカテゴリー変数と連続変数の関係。

③分散の分析：マルチカテゴリカテゴリ変数と連続変数の関係。

④** Chi-square test **：二分されたカテゴリー変数またはマルチクラスのカテゴリー変数と二分されたカテゴリー変数との関係。

この紹介：

線形回帰：複数の連続変数と1つの連続変数の間の関係。

その中で、線形回帰は単純線形回帰と多重線形回帰に分けられます。

/ 01 /データ分析とデータマイニング

データベース：データを保存するためのツール。 Pythonはメモリ計算であるため、数十のGデータを処理するのは困難であり、データベースでデータクリーニングを実行する必要がある場合があります。

統計：データサンプリング、記述分析、結果テストなど、小さなデータのデータ分析方法。

人工知能/機械学習/パターン認識：人間の神経系の動作を模倣するニューラルネットワークアルゴリズムは、トレーニングデータを通じて学習できるだけでなく、学習結果に基づいて未知のデータを予測することもできます。

/ 02 /回帰方程式

01 単純な線形回帰

単純な線形回帰には、1つの独立変数と1つの従属変数しかありません。

含まれるパラメータは、「回帰係数」、「インターセプト」、および「外乱項」です。

その中で、「外乱項」は「ランダムエラー」とも呼ばれ、平均が0の正規分布に従います。

従属変数の実際の値と線形回帰の予測値の差は、「残差」と呼ばれます。

**線形回帰は、残差の2乗の合計を最小化することを目的としています。 ****

以下は、本の場合の単純な線形回帰です。

収入と月間平均クレジットカード支出の予測モデルを確立します。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols

# パンダの出力の省略記号と改行を削除します
pd.set_option('display.max_columns',500)
pd.set_option('display.width',1000)
# データの読み取り,skipinitialspace:区切り文字の後の空白を無視する
df = pd.read_csv('creditcard_exp.csv', skipinitialspace=True)print(df.head())

データを読み取ります。データは次のとおりです。

データに対して相関分析を実行します。

# クレジットカードの支出のラインデータを取得する
exp = df[df['avg_exp'].notnull()].copy().iloc[:,2:].drop('age2', axis=1)
# 費用をかけずにクレジットカードの行データを取得する,NaN
exp_new = df[df['avg_exp'].isnull()].copy().iloc[:,2:].drop('age2', axis=1)
# 記述的統計分析
exp.describe(include='all')print(exp.describe(include='all'))
# 相関分析
print(exp[['avg_exp','Age','Income','dist_home_val']].corr(method='pearson'))

結果を出力します。

**収入（収入）と平均支出（avg_exp）**は、0.674の値で高度に相関していることがわかります。

単純な線形回帰を使用してモデルを構築します。

# 単純な線形回帰を使用してモデルを構築する
lm_s =ols('avg_exp ~ Income', data=exp).fit()print(lm_s.params)
# 出力モデルの基本情報,回帰係数とテスト情報,その他のモデル診断情報
print(lm_s.summary())

一項線形回帰係数の出力結果は以下のとおりです。

以上のことから、回帰係数の値は97.73、切片の値は258.05であることがわかります。

モデルの概要は以下のとおりです。

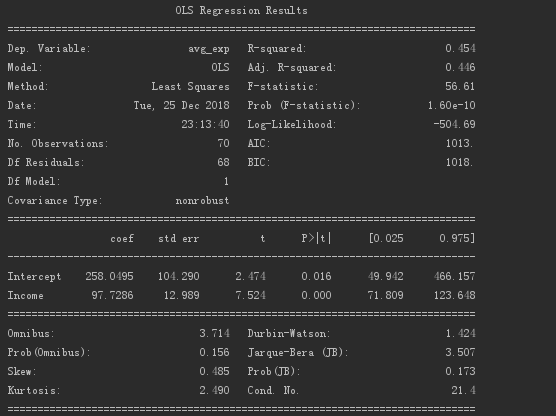
R²値は0.454であり、P値は0に近いため、モデルには依然として特定の参照重要性があります。

線形回帰モデルを使用してトレーニングデータセットをテストし、その予測値と残差誤差を取得します。

# 生成されたモデルはpredictを使用して予測値を生成します,residは、トレーニングデータセットの残差です。
print(pd.DataFrame([lm_s.predict(exp), lm_s.resid], index=['predict','resid']).T.head())

出力結果は、データが最初に読み取られたときの出力結果と比較できます。

モデルテストを使用して、データセットの結果を予測します。

# モデルを使用して、予測するデータセットを予測します
print(lm_s.predict(exp_new)[:5])

結果を出力します。

02 多重線形回帰

多重線形回帰は、単純な線形回帰に基づいており、独立変数が追加されています。

バイナリ線形回帰は、最も単純な多重線形回帰です。

1つの変数回帰が回帰線に適合し、次にバイナリ回帰が回帰平面に適合します。

多重線形回帰では、独立変数と従属変数の間の線形関係が必要であり、独立変数間の相関係数は可能な限り低くする必要があります。

回帰方程式の従属変数に線形に関連する独立変数が多いほど、回帰の解釈は強くなります。

方程式に非線形に関連する独立変数が多い場合、モデルの解釈は弱くなります。

調整されたR²（観測値の数とモデルの独立変数の数に関連）を使用して、回帰の長所と短所を評価できます。つまり、モデルの説明力を評価できます。

以下は、多重線形回帰を達成するための本の場合です。

顧客の年齢、年収、コミュニティハウスの平均価格、地域の1人当たりの収入、クレジットカードの月間平均支出の関係を分析します。

# 複数の線形回帰を使用してモデルを構築する
lm_m =ols('avg_exp ~ Age + Income + dist_home_val + dist_avg_income', data=exp).fit()print(lm_m.summary())

多重線形回帰モデルの情報は次のとおりです。

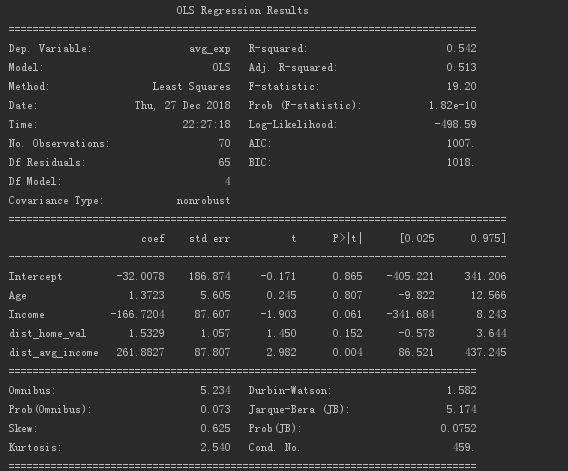
出力R²は0.542です。R²を0.513に調整してください。

方程式の有意性のテストP値（回帰係数がすべて0ではない）は1.82e-10であり、これは0に近く、回帰方程式に意味があることを示しています。

顧客の年齢と平均住宅価格の回帰係数は重要ではありません。

年収と一人当たりの地方所得の回帰係数は重要です。

多重線形回帰は、順方向法、逆方向法、および段階的方法に従って独立変数をフィルタリングできます。

順方向の方法は、変数を継続的に追加して回帰方程式を作成することであり、逆方向のルールは、変数を継続的に削除して回帰式を作成することです。段階的な方法は、追加と削除の2つの組み合わせです。

3つの方法は、** AIC基準（最小情報基準）に基づいており、 AIC値が小さいほど、モデルの効果が高くなり、**が簡潔になります。

AIC基準を使用すると、変数の増加が残差二乗和の減少とモデルの複雑さの増加の主な理由になるのを防ぐことができます。

今回は、順回帰法を使用して変数を継続的に加算し、加算された変数のAIC値を取得し、最終的に最も説明力のある変数を見つけます。

# フォワードリグレッション
def forward_select(data, response):"""データは、独立変数と従属変数を含むデータです,応答は従属変数です"""
 # 引数のリストを取得する
 remaining =set(data.columns)
 remaining.remove(response)
 selected =[]
 # データタイプを定義する(正の無限大)
 current_score, best_new_score =float('inf'),float('inf')
 # 引数リストに引数が含まれている場合
 while remaining:
  aic_with_candidates =[]
  # 引数のリストをループする
  for candidates in remaining:
   # 式を構築する,独立変数は増加し続けます
   formula ="{} ~ {}".format(response,' + '.join(selected +[candidates]))
   # 生成された独立変数のAIC解釈強度
   aic =ols(formula=formula, data=data).fit().aic
   # 独立変数のAIC説明強度リストを取得します
   aic_with_candidates.append((aic, candidates))
  # 解釈強度リストを最大から最小に並べ替えます
  aic_with_candidates.sort(reverse=True)
  # 説明された最大の強さを得る(最小AIC値)そして独立変数
  best_new_score, best_candidate = aic_with_candidates.pop()
  # 1. 正の無限大は最大説明力2より大きい.前の実験のAIC値は、次の実験のAIC値よりも大きくなければなりません,つまり、追加する変数が増える,AIC値は小さくする必要があります,より良いモデル
  if current_score > best_new_score:
   # 最も影響力のある独立変数を削除する
   remaining.remove(best_candidate)
   # 影響力のある独立変数を追加する
   selected.append(best_candidate)
   # この実験のAIC値を割り当てます
   current_score = best_new_score
   print('aic is {},continue!'.format(current_score))else:print('forward selection over!')break
 # 影響力のある独立変数のリストを使用する,データに対して線形回帰を実行します
 formula ="{} ~ {}".format(response,' + '.join(selected))print('final formula is {}'.format(formula))
 model =ols(formula=formula, data=data).fit()return model

# 順方向回帰を使用して変数をフィルタリングする,選択した変数を使用して回帰モデルを構築します
data_for_select = exp[['avg_exp','Income','Age','dist_home_val','dist_avg_income']]
lm_m =forward_select(data=data_for_select, response='avg_exp')print(lm_m.rsquared)

結果を出力します。

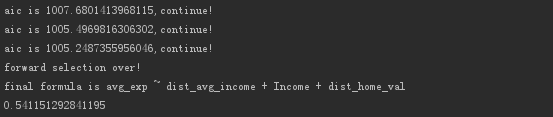
**顧客の年齢（年齢）**が排除され、最終的に線形回帰モデルが得られることがわかります。

/ 03 /まとめ

これは線形回帰モデルを構築しているだけで、有用であるとしか言えません。

モデルをより価値のあるものにするために、モデルは後で診断されます。

つづく...