Pythonはしきい値回帰を実装します

しきい値回帰モデル（TRモデルまたはTRM）の基本的な考え方は、しきい値変数の制御機能を使用することです。予測データが与えられると、しきい値変数のしきい値は、最初にしきい値変数のしきい値に従って制御機能を決定します。さまざまな予測式を使用して、ジャンプや突然の変化などのさまざまな現象を説明してみてください。その本質は、状態空間の値に従って予測問題を分類し、ピースワイズ線形回帰モデルを使用して、全体的な非線形予測問題を記述することです。

複数しきい値回帰のモデリングステップは、しきい値変数を確認し、しきい値番号L、しきい値、および回帰係数を較正するプロセスです。計算の便宜上、モデルのモデリングステップを説明するために2つの区分（つまりL = 2）が使用されます。

基本的な手順は次のとおりです（コード付き）：

データを読み取り、予測オブジェクトと予測係数の間の相関係数マトリックスを計算します。

読み取ったデータ
# パンダを使用してcsvを読み取ります。読み取られたデータはDataFrameオブジェクトです
data = pd.read_csv('jl.csv')
# DataFrameオブジェクトを配列に変換します,配列の最初の列はデータ番号、最後の列は予測オブジェクト、中央の列は予測係数です。
data= data.values.copy()
# print(data)
# 相互相関係数を計算します。パラメーターは予測子シーケンスと遅延時間kです。
def get_regre_coef(X,Y,k):
 S_xy=0
 S_xx=0
 S_yy=0
 # 予測係数と予測オブジェクトの平均値を計算します
 X_mean = np.mean(X)
 Y_mean = np.mean(Y)for i inrange(len(X)-k):
 S_xy +=(X[i]- X_mean)*(Y[i+k]- Y_mean)for i inrange(len(X)):
 S_xx +=pow(X[i]- X_mean,2)
 S_yy +=pow(Y[i]- Y_mean,2)return S_xy/pow(S_xx*S_yy,0.5)
# 相関係数行列を計算する
def regre_coef_matrix(data):
 row=data.shape[1]#列の数
 r_matrix=np.ones((1,row-2))
 # print(row)for i inrange(1,row-1):
 r_matrix[0,i-1]=get_regre_coef(data[:,i],data[:,row-1],1)#ラグタイムは1リターンr_matrix
r_matrix=regre_coef_matrix(data)
# print(r_matrix)
### 出力###
#[[0.0489790.078299890.190057050.275012090.28604638]]

相関係数がソートされ、相関係数が最大の係数がしきい値要素として使用されます。

# 相関係数を並べ替えて、しきい値要素として最大の相関係数を見つけます
def get_menxiannum(r_matrix):
 row=r_matrix.shape[1]#列の数
 for i inrange(row):if r_matrix.max()==r_matrix[0,i]:return i+1return-1
m=get_menxiannum(r_matrix)
# print(m)
## 出力##5番目の要素は最大の相関係数を持っています
#5

選択したしきい値要素係数に従ってデータを並べ替えます。

# しきい値要素に従って因子シーケンスをソートします,mはしきい値変数のシリアル番号です
def resort_bymenxian(data,m):
 data=data.tolist()#リストに変換
 data.sort(key=lambda x: x[m])#mによるリスト+並べ替える1列(上昇)
 data=np.array(data)return data
data=resort_bymenxian(data,m)#ソートされたシーケンス配列を取得します

ソートされたシーケンスは、しきい値要素に従って2つのセグメントに分割され、最初のセグメントは1データ、2番目のセグメントはn-1（nはサンプルサイズ）データ、2番目のセグメントは最初の2データ、 n-2データの2番目のセグメントである1回限りのアナロジーは、それぞれ分割されたF統計を計算し、最大の統計に対応するしきい値要素のセグメンテーションポイントをしきい値として選択します。

def get_var(x):return x.std()**2* x.size #総分散を計算する
# 統計Fの計算,入力データは、しきい値要素に従ってソートされた予測オブジェクトデータです。
def get_F(Y):
 col=Y.shape[0]#行数、サンプルサイズ
 FF=np.ones((1,col-1))#さまざまな分割点の統計を保存する
 V=get_var(Y)#総分散を計算する
 for i inrange(1,col):#1から列-1
 S=get_var(Y[0:i])+get_var(Y[i:col])#2つのセグメント内の分散の合計を計算します
 F=(V-S)*(col-2)/S
 FF[0,i-1]=F#この段階で、Fテストに合格したかどうかを判断する必要があり、F統計は合格後にのみ保持されます。
 return FF
y=data[:,data.shape[1]-1]
FF=get_F(y)
def get_index(FF,element):#1次元配列FFで最初に出現する要素のインデックスを取得します
 i=-1for item in FF.flat:
 i+=1if item==element:return i
f_index=get_index(FF,np.max(FF))#統計Fの最大のインデックスを取得します
# print(data[f_index,m-1])#しきい値要素は5番目の要素であり、インデックスに代入するとしきい値は121になります。

データシーケンスは、しきい値を分割点として2つのセグメントに分割され、それぞれ複数の線形回帰が実行されます。ここでは、sklearn.linear_modelモジュールの線形回帰モジュールが使用されます。予測因子を代入して、2つのセグメントの予測値をそれぞれ計算します。

# 新しいデータシーケンスを、しきい値を分割点として2つの部分に分割し、それぞれ重回帰計算を実行します
def data_excision(data,f_index):
 f_index=f_index+1
 data1=data[0:f_index,:]
 data2=data[f_index:data.shape[0],:]return data1,data2
data1,data2=data_excision(data,f_index)
# 第一段落
def get_XY(data):
 # 変数に値を割り当てるための配列スライス
 Y = data[:, data.shape[1]-1] #予測オブジェクトは最後の列にあります
 X = data[:,1:data.shape[1]-1]#2番目の列から最後から2番目の列への予測子
 return X, Y
X,Y=get_XY(data1)
regs=LinearRegression()
regs.fit(X,Y)
# print('第一段落')
# print(regs.coef_)#出力回帰係数
# print(regs.score(X,Y))#出力相関係数
# 予測値を計算する
Y1=regs.predict(X)
# print('2番目の段落')
X,Y=get_XY(data2)
regs.fit(X,Y)
# print(regs.coef_)#出力回帰係数
# print(regs.score(X,Y))#出力相関係数
# 予測値を計算する
Y2=regs.predict(X)
Y=np.column_stack((data[:,0],np.hstack((Y1,Y2)))).copy()
Y=np.column_stack((Y,data[:,data.shape[1]-1]))
Y=resort_bymenxian(Y,0)

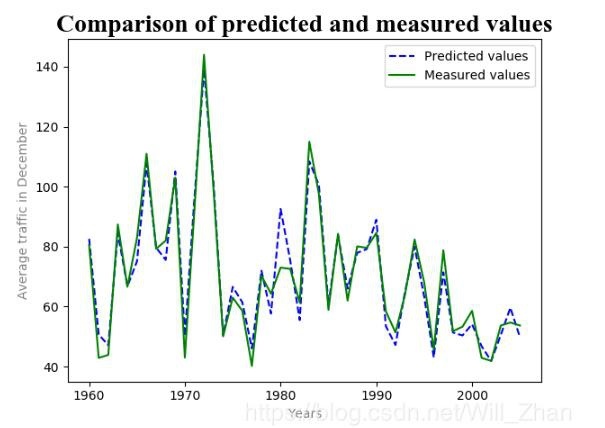
予測値と実際の値は年番号に従って再ソートされ、順序が復元され、matplotlibモジュールを使用して予測値と実際の値の比較チャートが作成されます。

# 回復命令
Y=resort_bymenxian(Y,0)
# print(Y.shape)
# 予測結果の視覚化
plt.plot(Y[:,0],Y[:,1],'b--',Y[:,0],Y[:,2],'g')
plt.title('Comparison of predicted and measured values',fontsize=20,fontname='Times New Roman')#表題を加える
plt.xlabel('Years',color='gray')#x軸ラベルを追加
plt.ylabel('Average traffic in December',color='gray')#y軸ラベルを追加
plt.legend(['Predicted values','Measured values'])#凡例を追加
plt.show()

結果グラフ：

使用したデータ：TangChengyouの公式記事であるZhangShimingによる「ModernMediumand Long-term Hydrological Forecasting MethodsandApplications」から引用

num	x1	x2	x3	x4	x5	y
1960	308	301	352	310	149	80.5
1961	182	186	165	127	70	42.9
1962	195	134	134	97	61	43.9
1963	136	378	334	307	148	87.4
1964	230	630	332	161	100	66.6
1965	225	333	209	365	152	82.9
1966	296	225	317	527	228	111
1967	324	229	176	317	153	79.3
1968	278	230	352	317	143	82
1969	662	442	453	381	188	103
1970	187	136	103	129	74.7	43
1971	284	404	600	327	161	92.2
1972	427	430	843	448	236	144
1973	258	404	639	275	156	98.9
1974	113	160	128	177	77.2	50.1
1975	143	300	333	214	106	63
1976	113	74	193	241	107	58.6
1977	204	140	154	90	55.1	40.2
1978	174	445	351	267	120	70.3
1979	93	95	197	214	94.9	64.3
1980	214	250	354	385	178	73
1981	232	676	483	218	113	72.6
1982	266	216	146	112	82.8	61.4
1983	210	433	803	301	166	115
1984	261	702	512	291	153	97.5
1985	197	178	238	180	94.2	58.9
1986	442	256	623	310	146	84.3
1987	136	99	253	232	114	62
1988	256	226	185	321	151	80.1
1989	473	409	300	298	141	79.6
1990	277	291	639	302	149	84.6
1991	372	181	174	104	68.8	58.4
1992	251	142	126	95	59.4	51.4
1993	181	125	130	240	121	64
1994	253	278	216	182	124	82.4
1995	168	214	265	175	101	68.1
1996	98.8	97	92.7	88	56.7	45.6
1997	252	385	313	270	119	78.8
1998	242	198	137	114	71.9	51.8
1999	268	178	127	109	68.6	53.3
2000	86.2	286	233	133	77.8	58.6
2001	150	168	122	93	62.8	42.9
2002	180	150	97.8	78	48.2	41.9
2003	166	203	166	124	70	53.7
2004	400	202	126	158	92.7	54.7
2005	79.8	82.6	129	160	76.6	53.7

上記のpythonしきい値回帰メソッドは、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。