Pythonデータサイエンス:ロジスティック回帰
データマイニングの内容を書いてから久しぶりですので、これからもお話させていただきます。
ロジスティック回帰モデルについて学びます。
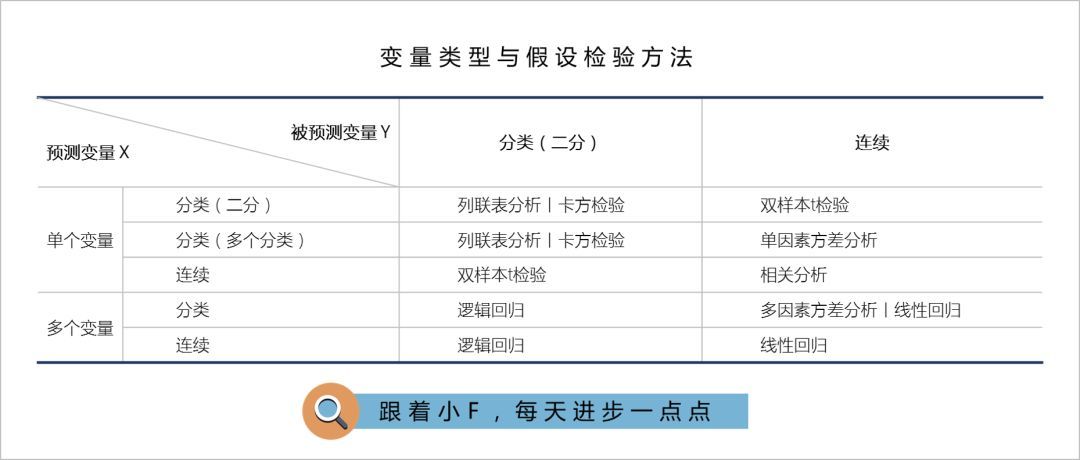
上の図から、従属変数がカテゴリ変数の場合、ロジスティック回帰モデルが主に使用されていることがわかります。
したがって、このデータ予測では、2つのカテゴリの変数(デフォルトかどうか)も選択されます。
/ 01 /ロジスティック回帰
ロジスティック回帰は、ロジット変換によって正または負の無限大を持つ線形方程式の値の範囲を(0、1)に変換します。これは、確率の値の範囲とまったく同じです。
特定の式はリストされていないので、ここで停止します。
もっと知りたい場合は、関連資料や本を参考にしてください。
ロジスティック回帰は、ロジット変換を構築することによって確率予測を行うことです。
線形回帰も予測方法です。
ただし、ロジスティック回帰はカテゴリ変数の予測に適しており、0から1までの間隔の確率を予測します。
線形回帰は、連続変数の予測に適しています。
さらに、ロジスティック回帰では、複数のターゲット変数がいつ検出されるかを予測することもできます。
しかし、多くの場合、アナリストは、ビジネスの理解に基づいて複数のターゲット変数をバイナリターゲット変数に統合し、ロジスティック回帰を実行する傾向があります(可能な場合)。
ロジスティック回帰は、イベントの確率を予測し、最大尤度推定を使用して確率のパラメーターを推定します。
/ 02 / Pythonの実装
慣例として、本で提供されているデータを引き続き使用してください。
車のデフォルトローンのデータセット。
関係する変数は、「デフォルト」、「破産マーク」、「5年間の不良クレジットイベントの数」、「最長アカウント期間」、「リサイクル可能なローンアカウント使用率」、「FICOスコア」、「ローン金額/推奨販売価格* 100」です。 「「駆動距離」。
データを読み取り、データをサンプリングします。トレーニングセットとテストセットの比率は7:3です。
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import sklearn.metrics as metrics
import statsmodels.formula.api as smf
# パンダの出力エリプシスを排除する
pd.set_option('display.max_columns', None)
# データの読み取り,skipinitialspace:区切り文字の後の空白を無視する
accepts = pd.read_csv('accepts.csv', skipinitialspace=True)
# dropna:不足しているデータを削除する
accepts = accepts.dropna(axis=0, how='any')
# フラックサンプリング比,70の場合%
train = accepts.sample(frac=0.7, random_state=1234).copy()
test = accepts[~ accepts.index.isin(train.index)].copy()print('トレーニングセットのサンプルサイズ: %i \nテストセットのサンプルサイズ: %i'%(len(train),len(test)))
いくつかの練習の後、抽出率が異なると最終結果も異なることがわかりました。
さらに、上記はランダムサンプリングを使用しており、トレーニングセットとテストセットのデフォルトの比率は異なります。
したがって、階層化されたサンプリングを検討して、サンプルの比率を固定することもできます。
次に、一般化された線形回帰が使用され、データを処理するためにロジット変換が指定されます。
lg = smf.glm('bad_ind ~ fico_score', data=train, family=sm.families.Binomial(sm.families.links.logit)).fit()print(lg.summary())
FICOスコアで得られたロジスティック回帰の結果。
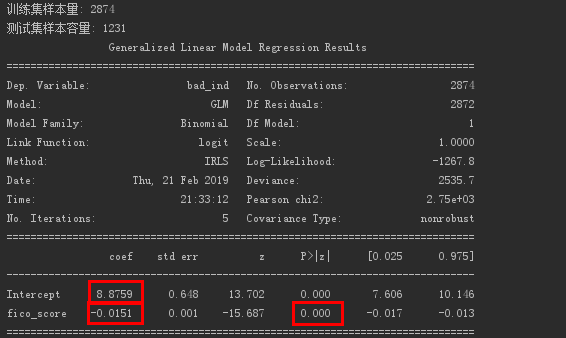
回帰方程式の係数と切片を取得します。
eの-0.0151乗の値は約0.985です。
これは、FICOスコアが1単位増加するたびに、デフォルトの確率が元の0.985倍になり、デフォルトの確率が減少することを意味します。
多重ロジスティック回帰の実現は以下のとおりです。
formula ="""bad_ind ~ fico_score + bankruptcy_ind + tot_derog + age_oldest_tr + rev_util + ltv + veh_mileage"""
lg_m = smf.glm(formula=formula, data=train, family=sm.families.Binomial(sm.families.links.logit)).fit()print(lg_m.summary())
得られたロジスティック回帰の結果は以下のとおりです。
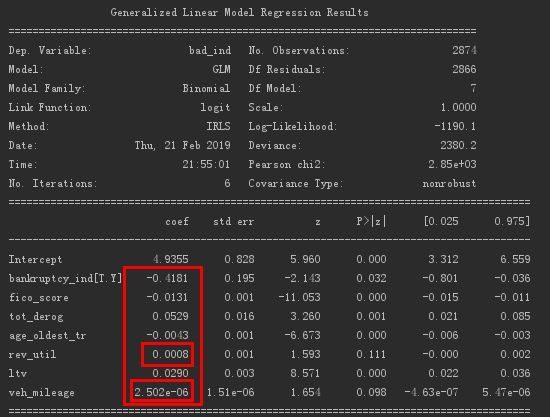
各変数の係数を取得します。その中で、「リサイクルローン口座使用率」と「走行距離」の2つの変数の係数は比較的重要ではなく、削除することができます。
もちろん、線形回帰で使用されるフォワードメソッドと組み合わせて、AIC基準に基づいて変数をフィルタリングすることもできます。
# フォワードリグレッション
def forward_select(data, response):"""データは、独立変数と従属変数を含むデータです,応答は従属変数です"""
# 引数のリストを取得する
remaining =set(data.columns)
remaining.remove(response)
selected =[]
# データタイプを定義する(正の無限大)
current_score, best_new_score =float('inf'),float('inf')
# 引数リストに引数が含まれている場合
while remaining:
aic_with_candidates =[]
# 引数のリストをループする
for candidates in remaining:
# 式を構築する,独立変数は増加し続けます
formula ="{} ~ {}".format(response,' + '.join(selected +[candidates]))
# 生成された独立変数のAIC解釈強度
aic = smf.glm(formula=formula, data=data, family=sm.families.Binomial(sm.families.links.logit)).fit().aic
# 独立変数のAIC説明強度リストを取得します
aic_with_candidates.append((aic, candidates))
# 説明強度リストを最大から最小に並べ替えます
aic_with_candidates.sort(reverse=True)
# 説明された最大の強さを得る(最小AIC値)そして独立変数
best_new_score, best_candidate = aic_with_candidates.pop()
# 1. 正の無限大は最大説明力2より大きい.前の実験のAIC値は、次の実験のAIC値よりも大きくなければなりません,つまり、追加する変数が増える,AIC値は小さくする必要があります,より良いモデル
if current_score > best_new_score:
# 最も影響力のある独立変数を削除する
remaining.remove(best_candidate)
# 影響力のある独立変数を追加する
selected.append(best_candidate)
# この実験のAIC値を割り当てます
current_score = best_new_score
print('aic is {},continue!'.format(current_score))else:print('forward selection over!')break
# 影響力のある独立変数のリストを使用する,データに対して線形回帰を実行します
formula ="{} ~ {}".format(response,' + '.join(selected))print('final formula is {}'.format(formula))
model = smf.glm(formula=formula, data=data, family=sm.families.Binomial(sm.families.links.logit)).fit()return model
# 順方向回帰を使用して変数をフィルタリングする,選択した変数を使用して回帰モデルを構築します
data_for_select = train[['bad_ind','fico_score','bankruptcy_ind','tot_derog','age_oldest_tr','rev_util','ltv','veh_mileage']]
lg_m1 =forward_select(data=data_for_select, response='bad_ind')print(lg_m1.summary())
出力は次のとおりです。
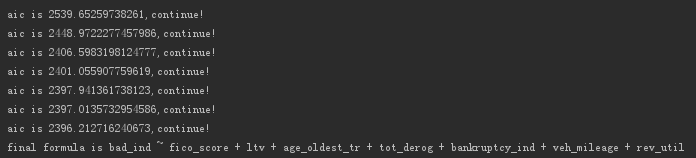
変数が除外されていないことがわかりました。
ただし、前述の2つの変数を観察すると、AIC値への変更は最小限です。
AIC値は減少していますが、変更に基づいて削除できます。
これは本とは異なります...
次に、線形回帰で分散展開係数計算関数を使用して、ロジスティック回帰での独立変数の多重共線性の判断を完了します。
def vif(df, col_i):
# 変数を取得する
cols =list(df.columns)
# 従属変数を削除する
cols.remove(col_i)
# 議論を得る
cols_noti = cols
# 多変量線形回帰モデルの確立および取得モデルR²
formula = col_i +'~'+'+'.join(cols_noti)
r2 = smf.ols(formula, df).fit().rsquared
# 分散展開係数を計算する
return1./(1.- r2)
# 独立変数データを取得する
exog = train[['fico_score','tot_derog','age_oldest_tr','rev_util','ltv','veh_mileage']]
# 引数を繰り返します,VIF値を取得する
for i in exog.columns:print(i,'\t',vif(df=exog, col_i=i))
出力は次のとおりです。

すべてがしきい値の10未満であることがわかります。これは、独立変数に有意な多重共線性がないことを示しています。
次に、トレーニング済みモデルを使用してテストを予測します。
train['proba']= lg_m1.predict(train)
test['proba']= lg_m1.predict(test)print(test['proba'].head())
# 0より大きい.デフォルトは5
test['prediction']=(test['proba']>0.5).astype('int')
# print(test['prediction'])
出力は次のとおりです。

/ 03 /モデル評価
ロジスティック回帰モデルは、主にランキングモデルとして使用されます。
ランキングモデルを評価するための指標には、ROC曲線、KS統計、ローレンツ曲線などがあります。
今回はROC曲線で示しています。
ROC曲線は、レシーバーの動作特性曲線とも呼ばれ、モデルの解像度能力を表すために使用されます。対角線より上のグラフが高いほど、モデルは優れています。
ROC曲線では、主に感度と特異性の2つの指標が含まれます。
感度は、モデルが応答をどれだけ適切に予測するかを示します。
特異性は、モデルが応答しないと予測するカバレッジの程度を示します。
カバレッジは、正確に予測された実際の観測の割合を示します。
ROC曲線は、X軸に特異性、Y軸に感度を持つ散乱曲線グラフです。
ROC曲線が急勾配であるほど、予測確率の高い観測での応答のカバレッジが強くなり、誤って報告された応答が少なくなり、モデルの効果が優れていることを示します。
最後に、AUC値(曲線の下の領域)を使用して、モデルの品質を判断できます。
「0.5、0.7」-効果は低い、「0.7、0.85」-効果は平均、「0.85、0.95」-効果は良い、「0.95、1」-効果は非常に良い。
この例のROC曲線の実装コードは次のとおりです。
acc =sum(test['prediction']== test['bad_ind'])/ np.float(len(test))
# モデルの精度を予測する
print('The accurancy is %.2f'% acc)
# 出力0.5つのしきい値でのクロスサマリーテーブル
print(pd.crosstab(test.bad_ind, test.prediction, margins=True))for i in np.arange(0,1,0.1):
prediction =(test['proba']> i).astype('int')
confusion_matrix = pd.crosstab(test.bad_ind, prediction, margins=True)
precision = confusion_matrix.ix[1,1]/ confusion_matrix.ix['All',1]
recall = confusion_matrix.ix[1,1]/ confusion_matrix.ix[1,'All']
f1_score =2*(precision * recall)/(precision + recall)print('threshold: %s, precision: %.2f, recall: %.2f, f1_score: %.2f'%(i, precision, recall, f1_score))
# ROC曲線を描く
fpr_test, tpr_test, th_test = metrics.roc_curve(test.bad_ind, test.proba)
fpr_train, tpr_train, th_train = metrics.roc_curve(train.bad_ind, train.proba)
plt.figure(figsize=[3,3])
plt.plot(fpr_test, tpr_test,'b--')
plt.plot(fpr_train, tpr_train,'r-')
plt.title('ROC curve')
plt.show()
# AUC値を計算する
print('AUC = %.4f'% metrics.auc(fpr_train, tpr_train))print(metrics.auc(fpr_train, tpr_train))
出力ROC曲線は次のとおりです。
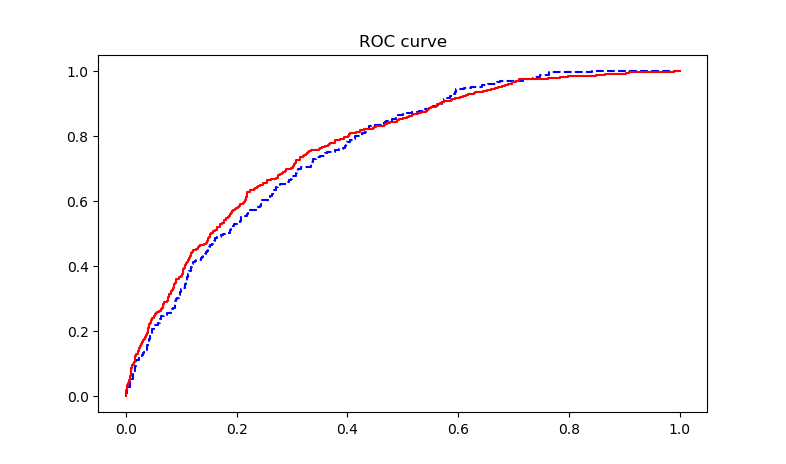
予測モデルの精度出力は0.81です。
出力AUC値は0.7732で、モデル効果は平均です。
Recommended Posts