Pythonの古典的なアルゴリズム

アルゴリズムの実装###

#0 GitHub

https://github.com/Coxhuang/Python-DataStructure

#1 周囲＃＃

Python3.7.3

#2 開始＃＃

#2.1 フィボナッチシーケンス###

GitHub

[ GitHubコード]（https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 ％95 / 1.Fibonacci）

問題の説明
法律
コード

従来の実装

def fib(max_val):
 a, b, n =0,1, max_val
 while n:print(a)
  a, b = b, a+b
  n -=1return None
fib(10)

出力

0112358132134

ビルダー

def fib(max_val):
 a, b, n =0,1, max_val
 while n:yield a
  a, b = b, a+b
  n -=1return None
for foo infib(10):print(foo)

出力

0112358132134

再帰

def fib(n):if n <2:return n
 returnfib(n-1)+fib(n-2)for foo inrange(10):print(fib(foo))

出力

0112358132134

#2.2 階段を上る###

GitHub

[ GitHubコード]（https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 ％95 / 2.％E5％8F％B0％E9％98％B6％E9％97％AE％E9％A2％98）

問題の説明

**カエルは一度に1レベルまたは2レベル（最大2レベル）までジャンプできます。nレベルにジャンプするカエルを見つける方法はいくつありますか？ ****

法律

**ステップが1つしかない場合は、1つの方法しかありません。2つのステップがある場合は、2つの方法があります。Nのステップがあり、最後にN番目のステップにジャンプする場合は、N-2から2つのステップに直接ジャンプできます。ステップ、またはN-1番目のステップから1ステップジャンプするため、Nステップのステップ数は、ステップN-2のメソッド数にステップN-1のメソッド数を加えたもの、つまりS（N ）= S（N-1）+ S（N-2）、初期項はS（1）= 1、S（2）= 2で、これはフィボナッチシーケンスに似ていますが、初期項が異なります。 ****

ステップ数	方法
f(0)	0
f(1)	1
f(2)	2
f(3)	3
f(4)	5
f(5)	8
…	…

論理法則はフィボナッチシーケンスと一致しています

コード

def fib(max_val):
 a, b, n =0,1, max_val
 while n:
  a, b = b, a+b
  n -=1return b
n =3 #ステップ数
ret = n if n <=2elsefib(n)print(ret)

#2.3 ジャンプステップ（異常ジャンプ）###

GitHub

[ GitHubコード]（https://github.com/Coxhuang/Python-DataStructure/tree/master/1.Algorithm/3.%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3 ％95 / 3.％E5％8F％B0％E9％98％B6％E9％97％AE％E9％A2％98％28％E5％8F％98％E6％80％81％E8％B7％B3％ 29）

問題の説明

**カエルは一度に1ステップまたは2ステップまでジャンプできます... nステップまでジャンプすることもできます。カエルがnレベルのステップでジャンプするジャンプ方法の総数を見つけます。 ****

法律

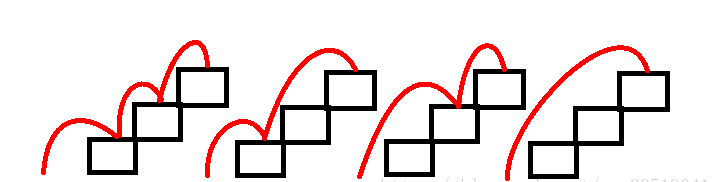
1ステップジャンプするとき、f(1)=1;2ステップジャンプする場合、f(2)=f(1)+1=2;3ステップジャンプするとき、f(3)=f(2)+f(1)+1=4;4ステップジャンプするとき、f(4)=f(3)+f(2)+f(1)+1=8;f(n-1)=f(n-2)+...+f(2)+f(1)+1f(n)=f(n-1)+f(n-2)+...+f(2)+f(1)+1

説明：

3.1. ここで、f（n）は、nステップが1、2、... nステップであるジャンプの数を表します。
3.2. n = 1の場合、ジャンプ方法は1つだけです。f（1）= 1
3.3. n = 2の場合、ジャンプする方法は2つあります。1つはステップ1または2で、問題（1）に戻ります。f（2）= f（2-1）+ f（2-2）
3.4. n = 3の場合、ジャンプする方法は1番目、2番目、3番目の3つで、最初のステージからジャンプするのは初めてで、残りは次のとおりです。f（3-1）; 2番目のステージからジャンプするのは初めて、残りのf （3-2）;最初は3ステップで、次にf（3-3）が残っているので、結論は次のようになります。

f(3)=f(3-1)+f(3-2)+f(3-3)

3.5. n = nの場合、nステップのジャンプ、1次、2次... n次があり、結論が導き出されます。

f(n)=f(n-1)+f(n-2)+...+f(n-(n-1))+f(n-n)=>f(0)+f(1)+f(2)+f(3)+...+f(n-1)

3.6. 上記は結論ですが、簡単にするために、引き続き簡単にすることができます。

f(n-1)=f(0)+f(1)+f(2)+f(3)+...+f((n-1)-1)=f(0)+f(1)+f(2)+f(3)+...+f(n-2)f(n)=f(0)+f(1)+f(2)+f(3)+...+f(n-2)+f(n-1)=f(n-1)+f(n-1)

3.7. 最終的な結論を導き出します。nステップに1、2、... nステップのステップがある場合、合計ジャンプ方法は次のようになります。

|1,( n=0)|f(n)=|1,(n=1)||2*f(n-1),(n>=2)

コード

# 再帰-方法1
def jump(n):while n<=2:return n
 returnjump(n-1)*2print(jump(5))

# 再帰-方法2
def jump(n):while n<=2:return n
 return2**(n-1)print(jump(5))

#2.4 ウサギの繁殖###

GitHub
問題の説明

**ウサギが2匹います。生後3ヶ月目から毎月1匹、小ウサギが3ヶ月目以降毎月1匹出産します。ウサギが死んでいない場合は、毎月ウサギに聞いてください。合計はいくらですか？ ****

アイデア

f（N）：Nか月のウサギの総数

f（Nbefore）：Nか月前に生まれたウサギ

f（新）：Nヶ月生まれのウサギ

f(N) = f(Nbefore) + f(Nnew) = f(N-1) + f(Nnew)

（N + 1）月に達すると：Nか月で生まれたウサギはまだ繁殖できず、Nか月より前に生まれたウサギはすべて繁殖できます

f(N+1) = f(Nnew) + f(Nbefore)2 = f(Nnew) + 2f(N-1)

沿って:f(N)=f(N-1)+f(Nnew)f(N+1)=f(Nnew)+2*f(N-1)

取得する:f(N+1)=f(N)+f(N-1)

コード

def fib(max_val):
 a, b, n =1,2, max_val
 while n:
  a, b = b, a+b
  n -=1return b
n =5 #N月
ret = n if n <=2elsefib(n)print(ret)

#2.5 重いリスト###

時間とスペースの複雑さの制限はありません

def func(tar):
 tar_copy =[]for foo in tar:if foo not in tar_copy:
   tar_copy.append(foo)return tar_copy
ret =func([1,2,2,2,2,3,4,5,6,7,8,9,8,1,2,3,4])print(ret)

時間の複雑さ

O(n)

スペースの複雑さ

O(n)

順序付きリスト+時間の複雑さO（n）+スペースの複雑さO（1）

forループは1つしか存在できないことを意味します+元のテーブルでのみ操作できます

def func(tar):for i,num inenumerate(tar):try: # tar[i+1]最後に例外をスローします
   while num == tar[i+1]:
    tar.pop(i+1)
  except:breakreturn tar
ret =func([1,1,1,2,2,2,2,3,3,4,4,5,6,7,8,8,9,9,9])print(ret)

つづく＃＃

Pythonリスト/辞書の操作時間の複雑さ
https://blog.csdn.net/Coxhuang/article/details/90313828