Pythonは10の古典的なソートアルゴリズムを実装しています

Pythonは10の古典的なソートアルゴリズムを実装しています＃

概要：

1. 操作モードでは、最後のコードをコピーして、pythonsort.pyを直接実行します。
2. コードの堅牢性に対処することはあまりないので、コードを直接使用する学生はそれを確認する必要があります。
3. ヒルソーティングの場合、ギャップの選択は非常に重要であり、実際の状況に応じて変更する必要があります。
4. 私のテストでは、ソートされる配列が非常に小さいため、長さは10のみで、最大値は10です。したがって、カウントソートが最速ですが、実際の状況ではそうではないことがよくあります。
5. ヒープソートを実装する時間がありませんでした、はい、それは怠惰です。
6. 重要なのは、アルゴリズムのアイデアを理解することです。実現に関しては、合理的な方法でアイデアを着陸させることだけです。
7. 上記のリンクにアクセスしてアニメーション画像を表示することをお勧めします。理解する方が確かに優れていますが、コードを読むこともお勧めします。
8. 分割と征服はよく使われます。実際、その背後にある数学的原理と、分割と征服が時間の複雑さを軽減できる理由はわかりません。一部の学生は、トラブルコメントセクションで私に言ってくれました。ありがとう。

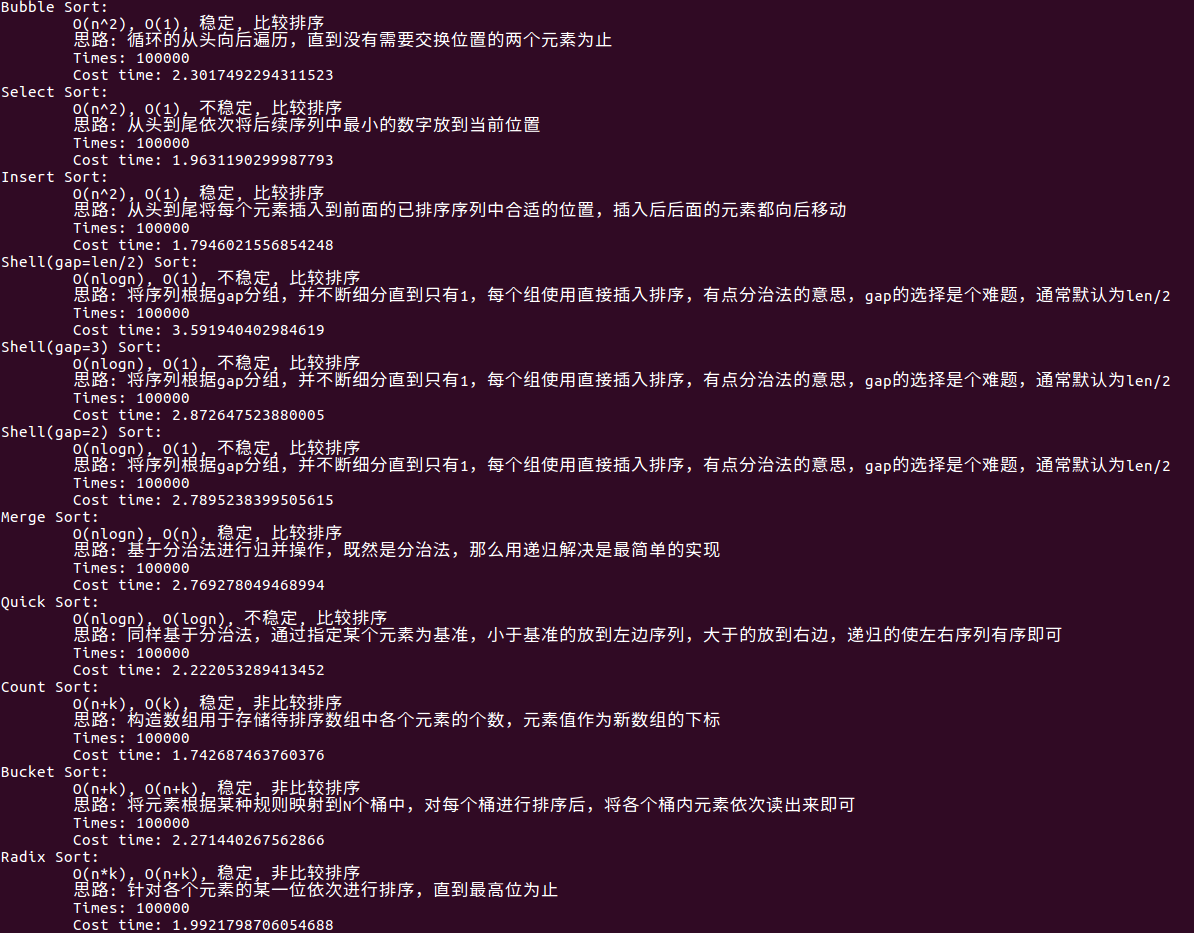
実行図##

配列が小さく、範囲が1〜10であるため、スペース圧力があまりないため、ソートをカウントする非比較アルゴリズムの方が実際には使いやすく、ソート速度のカウントが理解しやすく、選択する理由がわかります。 、挿入はヒルマージよりも高速です。これは主に、問題自体のサイズが小さすぎるためです。また、分割と征服の実装は再帰に基づいているため、分割と征服の利点がわかりません。実際、非常に大きな配列を並べ替えると、 、この違いが反映されます。

完全なコード##

ご覧のとおり、コード全体にはテストコードが含まれておらず、合計170行しかありません。これには空白行や関数名なども含まれているため、アルゴリズムの実装自体は非常に単純なので、誰もがアイデアに注意を払う必要があります。

import sys,random,time

def bubble(list_):
 running = True
 while running:
  have_change = False
  for i inrange(len(list_)-1):if list_[i]>list_[i+1]:
    list_[i],list_[i+1]= list_[i+1],list_[i]
    have_change = True
  if not have_change:breakreturn list_

def select(list_):for i inrange(len(list_)-1):
  min_idx = i
  for j inrange(i,len(list_)):if list_[min_idx]>list_[j]:
    min_idx = j
  list_[i],list_[min_idx]= list_[min_idx],list_[i]return list_

def insert(list_):for i inrange(1,len(list_)):
  idx = i
  for j inrange(i):if list_[j]>list_[idx]:
    idx = j
    breakif idx != i:
   tmp = list_[i]
   list_[idx+1:i+1]= list_[idx:i]
   list_[idx]= tmp
 return list_

def shell(list_,gap=None):'''
 ギャップの選択は結果に大きな影響を与えますが、これは難しい問題です。ヒルはlenを推奨しています。/2
 このギャップは実際にはギャップです。つまり、1つの要素グループによって分離されている要素の数です。
 たとえば[1,2,3,4,5,6,7,8,9,10]
 ギャップが長いとき/2が5の場合、各グループの要素は5つの要素、つまり1と6で構成されます。,2と7,3と8など。
    '''
 len_ =len(list_)
 gap =int(len_/2)if not gap else gap
 while gap >=1:for i inrange(gap):
   list_[i:len_:gap]=insert(list_[i:len_:gap])
  gap =int(gap/2)return list_

def merge(list_):'''
 マージソートの再帰的実装
 アイデア：データを2つのグループに分割してから、2つのグループを4つの要素のグループに分類します。
 シーケンス全体がトレースバックされるまで、実際には2つの順序付けられたサブシーケンスで構成されます。これは、典型的な再帰的な問題です。
    '''
 iflen(list_)<=1:return list_
 iflen(list_)==2:return list_ if list_[0]<=list_[1]else list_[::-1]
 len_ =len(list_)
 left =merge(list_[:int(len_/2)])
 right =merge(list_[int(len_/2):])
 tmp =[]
 left_idx,right_idx =0,0whilelen(tmp)<len(list_):if left[left_idx]<=right[right_idx]:
   tmp.append(left[left_idx])
   left_idx+=1if left_idx==len(left):
    tmp += right[right_idx:]breakelse:
   tmp.append(right[right_idx])
   right_idx+=1if right_idx==len(right):
    tmp += left[left_idx:]breakreturn tmp

def quick(list_):'''
 クイックソート：除算と征服の方法に基づいて、ベンチマークとして特定の要素を選択し、残りの要素をベンチマークの左右に配置します。このプロセスを再帰的に実行します。
    '''
 iflen(list_)<=1:return list_
 iflen(list_)==2:return list_ if list_[0]<=list_[1]else list_[::-1]
 base_idx =int(len(list_)/2)
 base = list_[base_idx]
 left =[]
 right =[]for i inrange(len(list_)):if i != base_idx:if list_[i]<= base:
    left.append(list_[i])else:
    right.append(list_[i])returnquick(left)+[base]+quick(right)

def count(list_):'''
 要素は整数である必要があります
    '''
 min_,max_ = list_[0],list_[0]for i inrange(1,len(list_)):if list_[i]<min_:
   min_ = list_[i]if list_[i]>max_:
   max_ = list_[i]
 count_list =[0]*(max_-min_+1)for item in list_:
  count_list[item-min_]+=1

 list_ =[]for i inrange(len(count_list)):for j inrange(count_list[i]):
   list_.append(i+min_)return list_

def heap(list_):'''

    '''
 pass

def bucket(list_):'''
 各バケットは選択的ソートを使用し、バケット化方法は最大値を5で割ったもので、5つのバケットに分割されます。
 バケットの並べ替えの速度は、バケットの並べ替え方法によって異なります
    '''
 bucket =[[],[],[],[],[]] #長さは5であることに注意してください
 max_ = list_[0]for item in list_[1:]:if item > max_:
   max_ = item
 gap = max_/5 #対応するバケットの長さ
 for item in list_:
  bucket[int((item-1)/gap)].append(item)for i inrange(len(bucket)):
  bucket[i]=select(bucket[i])
 list_ =[]for item in bucket:
  list_ += item
 return list_

def radix(list_):'''
 カーディナリティの並べ替え：1桁から始めて、10、100など、値のさまざまな桁を個別に並べ替えます。
 ここでのコードは、ソートされる値がすべて整数であることを前提としていることに注意してください
    '''
 max_ = list_[0]for item in list_[1:]:if item > max_:
   max_ = item
 max_radix =len(str(max_))
 radix_list =[[],[],[],[],[],[],[],[],[],[]] #各桁の9つの可能な番号に対応します
 cur_radix =0while cur_radix<max_radix:
  base =10**cur_radix
  for item in list_:
   radix_list[int(item/base)%10].append(item)
  list_ =[]for item in radix_list:
   list_ += item

  radix_list =[[],[],[],[],[],[],[],[],[]] #各桁の9つの可能な番号に対応します
  cur_radix +=1return list_

def test(name,sort_func,times,info,idea,*param):
 list_ =[1,2,3,4,5,6,7,8,9,10]print(name+' Sort:')print('\t'+info)print('\t'+idea)print('\tTimes: '+str(times))
 start_time = time.time()for i inrange(times):
  random.shuffle(list_)
  # print('\tInput: '+str(list_))
  list_ =sort_func(list_)iflen(param)<=0elsesort_func(list_,param[0])
  # print('\tOutput: '+str(list_))
 # print('\t'+str(list_))print('\tCost time: '+str(time.time()-start_time))if __name__ =="__main__":test('Bubble',bubble,100000,'O(n^2), O(1),安定,比較ソート','アイデア:交換する必要のある2つの要素がなくなるまで、最初から前後にループします')test('Select',select,100000,'O(n^2), O(1),不安定,比較ソート','アイデア:後続のシーケンスの最小数を最初から最後まで現在の位置に配置します')test('Insert',insert,100000,'O(n^2), O(1),安定,比較ソート','アイデア:各要素を最初から最後まで、前のソートされたシーケンスの適切な位置に挿入すると、後続のすべての要素は挿入後に後方に移動します')test('Shell(gap=len/2)',shell,100000,'O(nlogn), O(1),不安定,比較ソート','アイデア:シーケンスはギャップに従ってグループ化され、1つになるまで継続的に細分化されます。各グループは直接挿入ソートを使用します。これは、少しの分割と征服を意味します。ギャップの選択は難しい問題であり、通常、デフォルトはlenです。/2')test('Shell(gap=3)',shell,100000,'O(nlogn), O(1),不安定,比較ソート','アイデア:シーケンスはギャップに従ってグループ化され、1つになるまで継続的に細分化されます。各グループは直接挿入ソートを使用します。これは、少しの分割と征服を意味します。ギャップの選択は難しい問題であり、通常、デフォルトはlenです。/2',3)test('Shell(gap=2)',shell,100000,'O(nlogn), O(1),不安定,比較ソート','アイデア:シーケンスはギャップに従ってグループ化され、1つになるまで継続的に細分化されます。各グループは直接挿入ソートを使用します。これは、少しの分割と征服を意味します。ギャップの選択は難しい問題であり、通常、デフォルトはlenです。/2',2)test('Merge',merge,100000,'O(nlogn), O(n),安定,比較ソート','アイデア:除算と征服の方法に基づくマージ操作、除算と征服の方法であるため、再帰的ソリューションが最も簡単な実装です')test('Quick',quick,100000,'O(nlogn), O(logn),不安定,比較ソート','アイデア:また、除算と征服の方法に基づいて、特定の要素をベンチマークとして指定することにより、ベンチマークよりも小さいものを左のシーケンスに配置し、ベンチマークよりも大きいものを右に配置し、左右のシーケンスを再帰的に並べます。')
 # test('Heap',heap,100000,'O(nlogn), O(1),不安定,比較ソート','アイデア:ヒープの性質を使用して、完全なバイナリツリーを構築します')test('Count',count,100000,'O(n+k), O(k),安定,非比較ソート','アイデア:並べ替える配列の要素数を格納する配列を作成し、要素値を新しい配列の添え字として使用します')test('Bucket',bucket,100000,'O(n+k), O(n+k),安定,非比較ソート','アイデア:特定のルールに従って要素をN個のバケットにマップし、各バケットを並べ替えた後、各バケットの要素を順番に読み取ります。')test('Radix',radix,100000,'O(n*k), O(n+k),安定,非比較ソート','アイデア:各要素を最も高い位置まで順番に並べ替えます')

 # print(heap([4,6,8,3,5,10,9,2,1,7]))