IOU計算ケースのPython実装

2つの長方形の交差率の計算は、通常、検出タスクの検出インデックスとして使用されます。予測されたbboxとgroundtruthの違いは、IOUを通じて反映できます。非常に単純なアルゴリズムの実装です。私も何気なく、非常に単純なものを作成しました。

使用する際は、bbox内の4つの数字（y0、x0、y1、x1）の順序に注意してください。順序は同じではありません。

#! /usr/bin/env python
# encoding: utf-8
 
def compute_iou(rec1, rec2):"""
 computing IoU
 : param rec1:(y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2:(y0, x0, y1, x1):return: scala value of IoU
  """
 # computing area of each rectangles
 S_rec1 =(rec1[2]- rec1[0])*(rec1[3]- rec1[1])
 S_rec2 =(rec2[2]- rec2[0])*(rec2[3]- rec2[1])
 
 # computing the sum_area
 sum_area = S_rec1 + S_rec2
 
 # find the each edge of intersect rectangle
 left_line =max(rec1[1], rec2[1])
 right_line =min(rec1[3], rec2[3])
 top_line =max(rec1[0], rec2[0])
 bottom_line =min(rec1[2], rec2[2])
 
 # judge if there is an intersect
 if left_line  = right_line or top_line  = bottom_line:return0else:
 intersect =(right_line - left_line)*(bottom_line - top_line)return(intersect /(sum_area - intersect))*1.0if __name__=='__main__':
 rect1 =(661,27,679,47)
 # ( top, left, bottom, right)
 rect2 =(662,27,682,47)
 iou =compute_iou(rect1, rect2)print(iou)

補足知識：Pythonに基づくIOUアルゴリズム-最も単純で理解しやすいコード実装

コンセプト紹介：

連合を越えた交差点:(連合を越えた交差点）

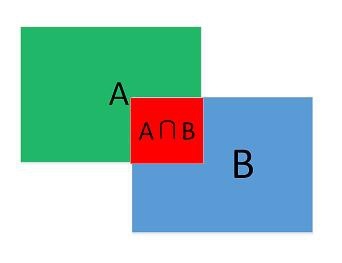
上図に示すように、IOU値は、2つの長方形のボックスの領域の交差と結合の比率として配置されます。これは：

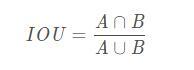
相互比較の実装も非常に簡単で、実行プロセスは次のとおりです。

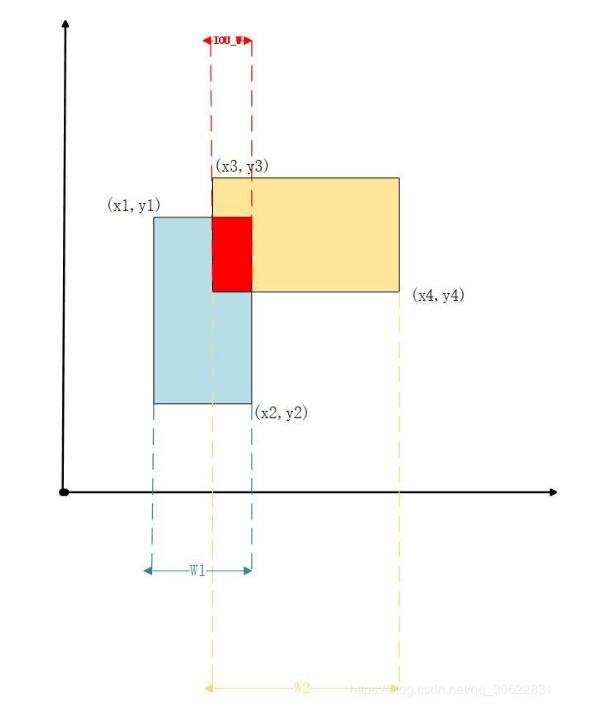
交差形状の幅は次のように計算されます。

IOU_W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)

交差形状の高さは次のように計算されます。

IOU_H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)

実際、これは非常に単純な幾何学的関係の変換です。上の図は、この意味をよく理解するのに役立ちます。

コードの実装：001-IOU計算

上記のIOU計算ケースのpython実装は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。