Pythonの9つの機能エンジニアリング手法

この記事に添付されているコードはここにあります。

https://github.com/NMZivkovic/top_9_feature_engineering_techniques

この記事では、良好な結果を得るために通常必要とされる最も効果的な要素エンジニアリング手法について説明します。

誤解しないでください。機能設計はモデルを最適化するだけではありません。データが機械学習アルゴリズムと互換性を持つように、これらの手法を適用する必要がある場合があります。機械学習アルゴリズムは、特定の方法でデータをフォーマットすることを期待する場合があります。これは、機能エンジニアリングが役立つ場合があります。さらに、データ科学者とエンジニアはほとんどの時間をデータの前処理に費やしていることに注意してください。これが、これらのテクノロジーを習得することが重要である理由です。この記事で調べてください：

データセットと前提条件

このチュートリアルでは、次のPythonライブラリがインストールされていることを確認してください。

インストールが完了したら、このチュートリアルで使用する必要なモジュールがすべてインポートされていることを確認してください。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sb
 
from sklearn.preprocessing import StandardScaler, MinMaxScaler, MaxAbsScaler, QuantileTransformer
from sklearn.feature_selection import SelectKBest, f_classif

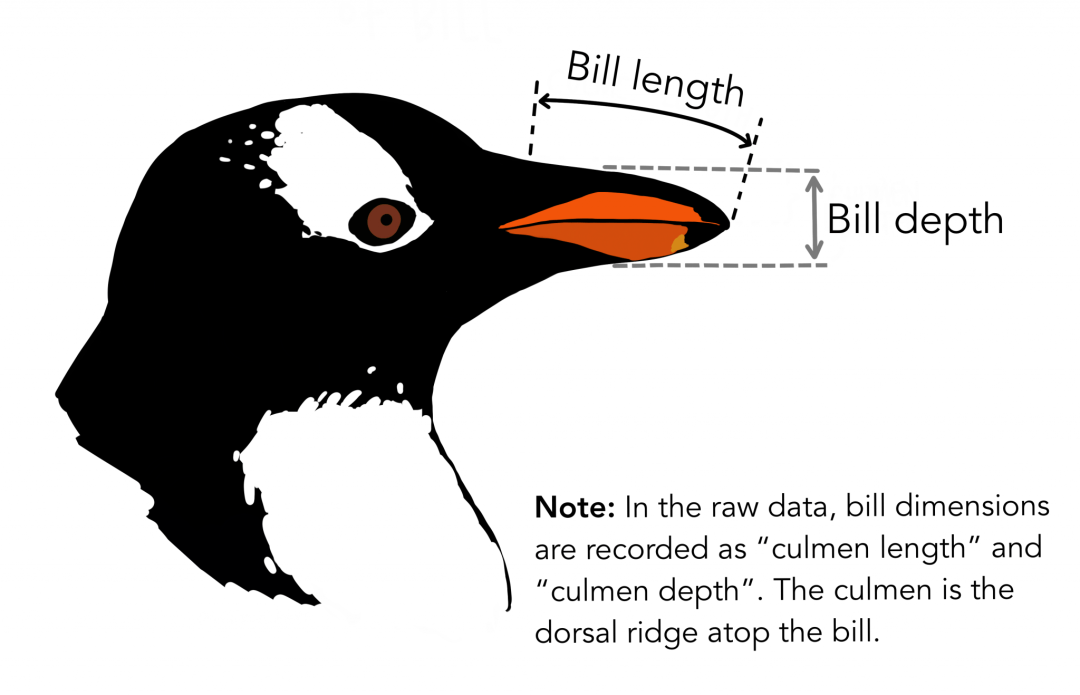
この記事で使用されているデータは、PalmerPenguinsデータセットからのものです。このデータセットは、有名なアイリスデータセットを置き換えるために最近導入されました。それは、南極のクリステン・ゴーマン博士とパーマー・ステーションによって作成されました。このデータセットは、ここまたはKaggleから入手できます。このデータセットは基本的に2つのデータセットで構成され、各データセットには344個のペンギンのデータが含まれています。アイリスデータセットと同様に、パーマー諸島の3つの島には3つの異なるペンギンがあります。

https://github.com/allisonhorst/palmerpenguins

繰り返しますが、これらのデータセットには各種の標本寸法が含まれています。高い門はくちばしの上部の尾根です。簡略化されたペンギンデータでは、頂点の長さと深さがculmen_length_mm変数とculmen_depth_mm変数に名前が変更されています。 Pandasを使用して、このデータセットをロードします。

data = pd.read_csv('./data/penguins_size.csv')
data.head()

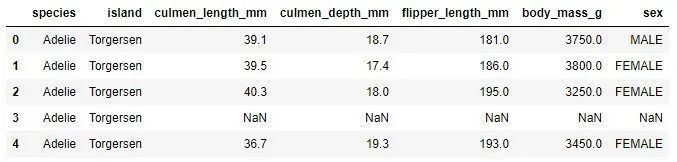
1. アトリビューション

お客様から入手したデータは、さまざまな形をとることができます。通常はまばらです。つまり、一部のサンプルでは特定の機能のデータが不足している可能性があります。これらのインスタンスを検出してこれらのサンプルを削除するか、null値を何らかの値に置き換える必要があります。データセットの残りの部分に応じて、これらの欠落した値を置き換えるために異なる戦略が適用される場合があります。たとえば、これらの空のスロットは、平均または最大の固有値で埋めることができます。ただし、最初に欠落しているデータを検出します。あなたはこれのためにパンダを使うことができます：

print(data.isnull().sum())

これは、特定の要素の値が不足しているインスタンスがデータセットにあることを意味します。 2つのインスタンスにはculmen_length_mm機能値がなく、10のインスタンスには性別機能がありません。最初のいくつかの例でも見ることができます（NaNは数値ではないことを意味し、値が欠落していることを意味します）。

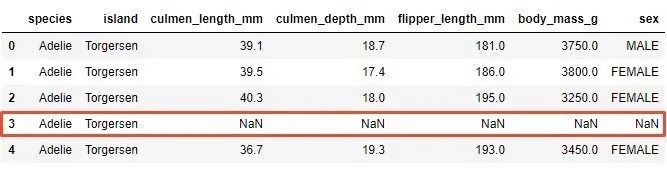
欠落している値を処理する最も簡単な方法は、欠落している値を持つサンプルをデータセットから削除することです。実際、一部の機械学習プラットフォームでは、これが自動的に行われます。ただし、データセットが減少するため、データセットのパフォーマンスが低下する可能性があります。パンダを再度使用するのが最も簡単な方法です。

data = pd.read_csv('./data/penguins_size.csv')
data = data.dropna()
data.head()

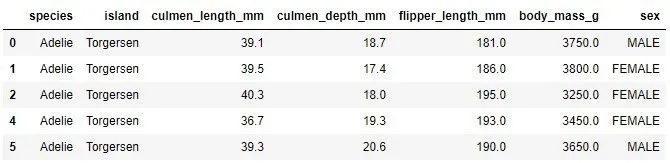
値が欠落している3番目のサンプルがデータセットから削除されていることに注意してください。これは最良の選択ではありませんが、ほとんどの機械学習アルゴリズムはまばらなデータには適していないため、必要になる場合があります。もう1つの方法は、欠落している値を置き換えるインピュテーションを使用することです。これを行うには、いくつかの値を選択するか、平均固有値、または平均固有値などを使用できます。そして、あなたは注意しなければなりません。インデックス3の行の欠落している値を観察します。

単純な値のみに置き換えると、同じ値がカテゴリと数値の特徴に適用されます：

data = data.fillna(0)

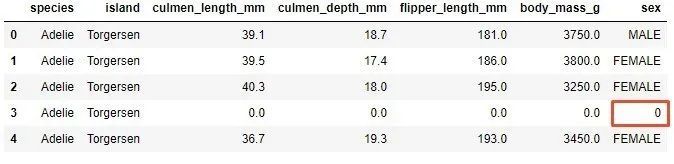
欠落しているデータは、デジタル機能culmen_length_mm、culmen_depth_mm、flipper_length_mm、およびbody_mass_gで検出されました。これらの機能の推定値には、機能の平均値が使用されます。 「性別」の分類機能では、最も頻度の高い値が使用されます。これは方法です：

data = pd.read_csv('./data/penguins_size.csv')
 
data['culmen_length_mm'].fillna((data['culmen_length_mm'].mean()), inplace=True)
data['culmen_depth_mm'].fillna((data['culmen_depth_mm'].mean()), inplace=True)
data['flipper_length_mm'].fillna((data['flipper_length_mm'].mean()), inplace=True)
data['body_mass_g'].fillna((data['body_mass_g'].mean()), inplace=True)
 
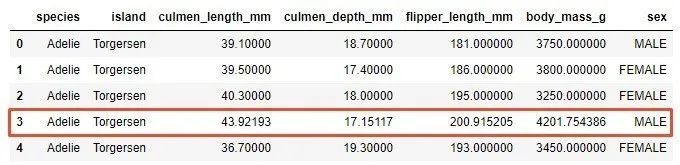
data['sex'].fillna((data['sex'].value_counts().index[0]), inplace=True)
 
data.reset_index()
data.head()

今述べた3番目の例がどのように見えるかを観察してください：

通常、データは失われませんが、その値は無効です。たとえば、「gender」関数には、FEMALEとMALEの2つの値が存在する可能性があることに注意してください。他の値があるかどうかを確認できます。

data.loc[(data['sex']!='FEMALE')&(data['sex']!='MALE')]

値が「。」のレコードがあることがわかりました。この関数の場合、これは正しくありません。これらのインスタンスを失われたデータとして扱い、それらを破棄または置換できます。

data = data.drop([336])
data.reset_index()

2. 分類コード

予測を改善する1つの方法は、カテゴリ変数を処理するときに巧妙な方法を使用することです。名前が示すように、これらの変数は個別の値を持ち、特定のカテゴリを表します。たとえば、色はカテゴリ変数（ "red"、 "blue"、 "green"）にすることができます。課題は、これらの変数をデータ分析に含め、機械学習アルゴリズムで使用することです。一部の機械学習アルゴリズムは、さらに操作しなくてもカテゴリ変数をサポートできますが、サポートできないものもあります。これが、分類コードを使用する理由です。このチュートリアルでは、いくつかのタイプの分類コードを紹介しますが、先に進む前に、データセット内のこれらの変数の個々の変数への変換を抽出し、分類タイプとしてマークします。

data["species"]= data["species"].astype('category')
data["island"]= data["island"].astype('category')
data["sex"]= data["sex"].astype('category')
data.dtypes

categorical_data = data.drop(['culmen_length_mm','culmen_depth_mm','flipper_length_mm', \
  ' body_mass_g'], axis=1)
categorical_data.head()

さて、今から始めることができます。最も単純なコーディングラベルコーディングから始めます。

2.1 ラベルコーディング

ラベルエンコーディングは、各カテゴリ値をいくつかの数値に変換します。たとえば、「種」関数には3つのカテゴリが含まれています。値0をAdelieに、1をGentooに、2をChinstrapに割り当てることができます。この手法を実行するには、Pandasを使用できます。

categorical_data["species_cat"]= categorical_data["species"].cat.codes
categorical_data["island_cat"]= categorical_data["island"].cat.codes
categorical_data["sex_cat"]= categorical_data["sex"].cat.codes
categorical_data.head()

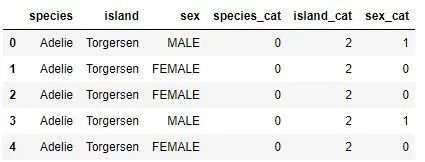
ご覧のとおり、3つの新しい関数が追加され、それぞれにコード化された分類関数が含まれています。最初の5つの例から、種カテゴリAdelieのコード値は0、島カテゴリTorgensnのコード値は2、性別カテゴリFEMALEとMALEのコード値はそれぞれ0と1であることがわかります。

2.2 ワンクリックコーディング

これは、最も一般的な分類コーディング手法の1つです。 1つの機能の値を複数のフラグ機能に分散し、0または1の値を割り当てます。バイナリ値は、コード化されていない機能とコード化された機能の関係を表します。

たとえば、データセットでは、「性別」関数に2つの可能な値があります：女性と男性。このテクノロジーは、「sex_female」と「sex_male」というラベルの付いた2つの別個の関数を作成します。 「sex」機能に値「いくつかのサンプルとしての女性」がある場合、「sex_female」には値1が割り当てられ、「sex_male」には値0が割り当てられます。同様に、「sex」の機能で、一部のサンプルでは、値「MALE」に「sex_male」に値1が割り当てられ、「sex_female」に値0が割り当てられます。この手法を分類されたデータに適用して、何が得られるかを確認します。

encoded_spicies = pd.get_dummies(categorical_data['species'])
encoded_island = pd.get_dummies(categorical_data['island'])
encoded_sex = pd.get_dummies(categorical_data['sex'])
 
categorical_data = categorical_data.join(encoded_spicies)
categorical_data = categorical_data.join(encoded_island)
categorical_data = categorical_data.join(encoded_sex)

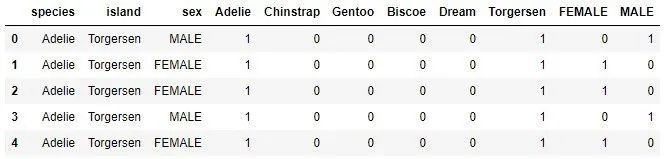
ここにいくつかの新しい列を追加するとき。本質的に、各関数の各カテゴリには個別の列があります。通常、機械学習アルゴリズムの入力として使用されるのは、ホットコード化された値のみです。

2.3 カウントコード

カウントコーディングは、各カテゴリ値をその頻度、つまりデータセットに表示される回数に変換します。たとえば、「species」関数にAdelieクラスが6回含まれている場合、各Adelie値は番号6に置き換えられます。これは、コードでどのように機能するかです。

categorical_data = data.drop(['culmen_length_mm','culmen_depth_mm', \
  ' flipper_length_mm','body_mass_g'], axis=1)
 
species_count = categorical_data['species'].value_counts()
island_count = categorical_data['island'].value_counts()
sex_count = categorical_data['sex'].value_counts()
 
categorical_data['species_count_enc']= categorical_data['species'].map(species_count)
categorical_data['island_count_enc']= categorical_data['island'].map(island_count)
categorical_data['sex_count_enc']= categorical_data['sex'].map(sex_count)
 
categorical_data

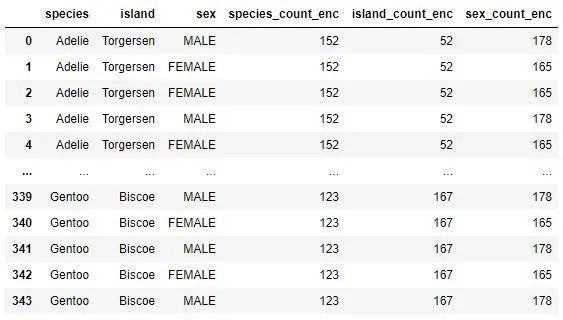
各カテゴリ値を出現回数に置き換える方法に注意してください。

2.4 ターゲットエンコーディング

以前のテクノロジーとは異なり、このテクノロジーは少し複雑です。これは、平均化された出力を、機能の値としてのカテゴリ値（つまり、ターゲット）に置き換えます。基本的に行う必要があるのは、特定のカテゴリ値を持つすべての行の平均出力を計算することです。出力値が数値の場合、これは非常に簡単です。たとえばPalmerPenguinsデータセットで出力が分類されている場合は、以前のいくつかの手法を適用する必要があります。

通常、この平均値は、めったに発生しない値の変動を減らすために、データセット全体の結果確率と混合されます。カテゴリ値は出力値に基づいて計算されるため、これらの計算はトレーニングデータセットに対して実行してから、他のデータセットに適用する必要があることに注意してください。そうしないと、情報漏えいに直面することになります。つまり、テストセットの出力値に関する情報がトレーニングセットに含まれることになります。これにより、テストが無効になるか、誤った信頼が得られます。コードでこれを行う方法をよく見てください。

categorical_data["species"]= categorical_data["species"].cat.codes
 
island_means = categorical_data.groupby('island')['species'].mean()
sex_means = categorical_data.groupby('sex')['species'].mean()

ここでは、出力フィーチャにラベルエンコーディングを使用し、分類フィーチャ「island」と「gender」の平均値を計算します。これは「島」機能の理解です：

island_means

これは、Biscoe、Dream、Torgersenの値がそれぞれ1.473054、0.548387、0の値に置き換えられることを意味します。 「性別」機能についても、同様の状況があります。

sex_means

これは、値FEMALEとMALEがそれぞれ0.909091と0.921348に置き換えられることを意味します。データセットは次のようになります。

categorical_data['island_target_enc']= categorical_data['island'].map(island_means)
categorical_data['sex_target_enc']= categorical_data['sex'].map(sex_means)
categorical_data

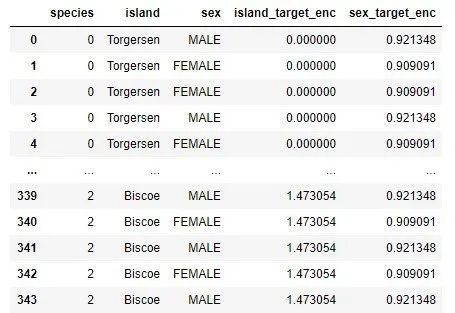
2.5 ターゲットコードを保持する

このチュートリアルで説明する最終的なエンコーディングタイプは、ターゲットエンコーディングに基づいています。ターゲットエンコーディングと同じように機能しますが、異なります。サンプルの平均出力値を計算するときは、サンプルを除外してください。これは、コードで行われる方法です。まず、この操作を実行する関数を定義します。

def leave_one_out_mean(series):
series =(series.sum()- series)/(len(series)-1)return series

次に、それをデータセットの分類値に適用します。

categorical_data['island_loo_enc']= categorical_data.groupby('island')['species'].apply(leave_one_out_mean)
categorical_data['sex_loo_enc']= categorical_data.groupby('sex')['species'].apply(leave_one_out_mean)
categorical_data

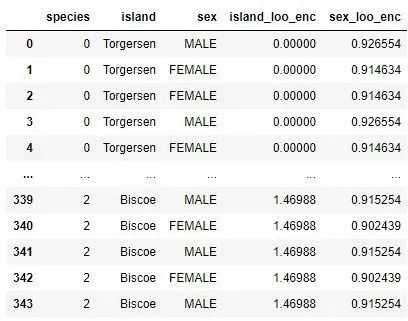
3. 異常値の処理

異常値は、データの全体的な分布から逸脱した値です。これらの値は、間違った測定値や間違った測定値であり、データセットから削除する必要がある場合もありますが、貴重なエッジケース情報である場合もあります。つまり、重要な情報が含まれている可能性があるため、これらの値をデータセットに保持したい場合もあれば、情報エラーのためにこれらのサンプルを削除したい場合もあります。

つまり、四分円間範囲を使用してこれらのポイントを検出できます。四分位範囲またはIQRは、データの50％がどこにあるかを示します。この値を探すときは、データを半分に分割するため、最初に中央値を探します。次に、データの下限の中央値（Q1と表示）とデータの上限の中央値（Q3と表示）を見つけます。 Q1とQ3の間のデータはIQRです。異常値は、Q1 – 1.5（IQR）未満またはQ3 + 1.5（IQR）を超えるサンプルとして定義されます。ボックスプロットを使用できます。ボックスプロットの目的は、分布を視覚化することです。基本的に、重要なポイントが含まれています。最大、最小、中央、および2つのIQRポイント（Q1、Q3）です。以下は、ボックスプロットの例です。

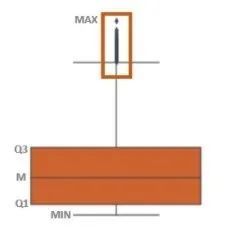
それをPalmerPenguinsデータセットに適用します。

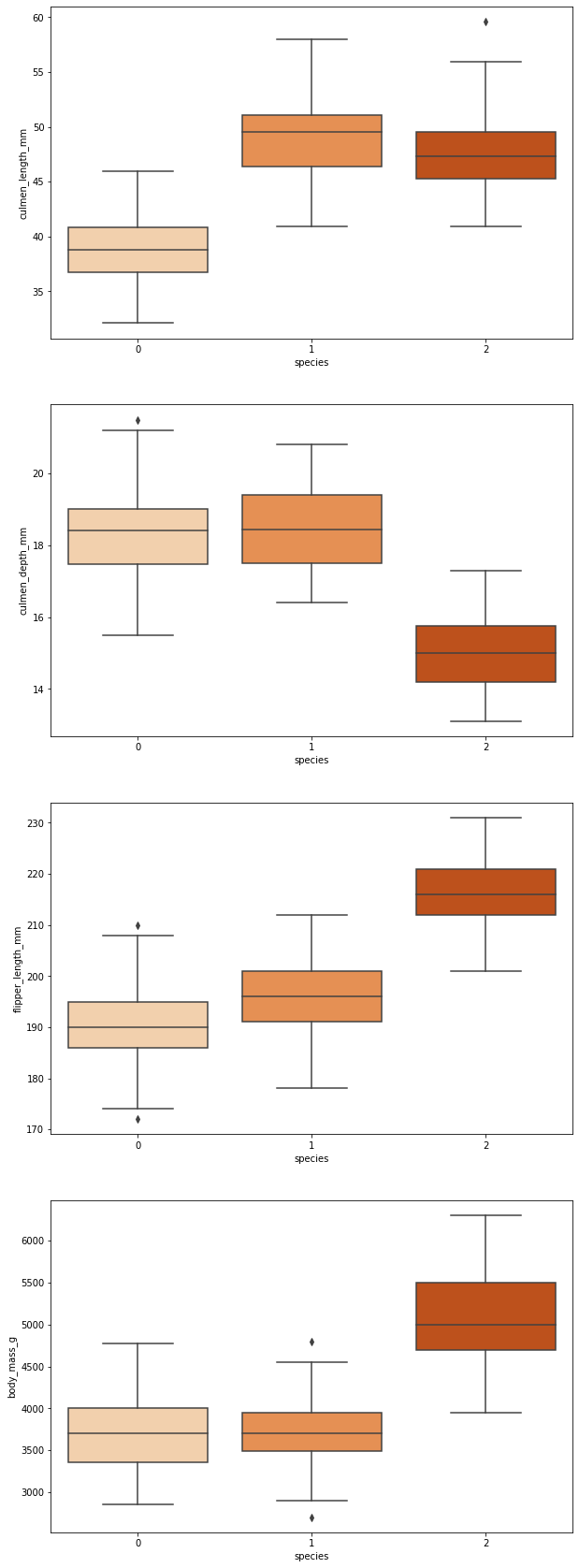
fig, axes = plt.subplots(nrows=4,ncols=1)
fig.set_size_inches(10,30)
sb.boxplot(data=data,y="culmen_length_mm",x="species",orient="v",ax=axes[0], palette="Oranges")
sb.boxplot(data=data,y="culmen_depth_mm",x="species",orient="v",ax=axes[1], palette="Oranges")
sb.boxplot(data=data,y="flipper_length_mm",x="species",orient="v",ax=axes[2], palette="Oranges")
sb.boxplot(data=data,y="body_mass_g",x="species",orient="v",ax=axes[3], palette="Oranges")

異常値を検出して排除する別の方法は、標準偏差を使用することです。

factor =2
upper_lim = data['culmen_length_mm'].mean()+ data['culmen_length_mm'].std()* factor
lower_lim = data['culmen_length_mm'].mean()- data['culmen_length_mm'].std()* factor
 
no_outliers = data[(data['culmen_length_mm']< upper_lim)&(data['culmen_length_mm']> lower_lim)]
no_outliers

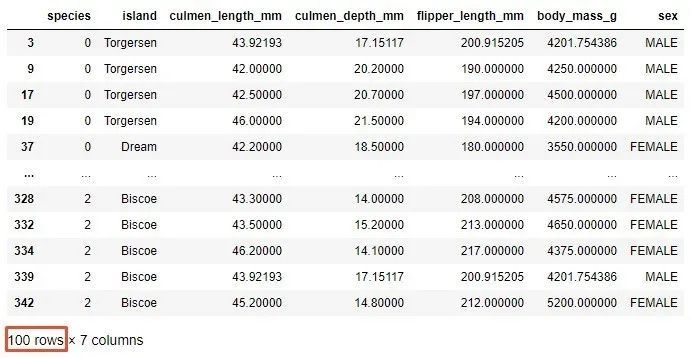
この操作の後に残っているサンプルは100個だけであることに注意してください。ここでは、標準偏差を掛けた係数を定義する必要があります。通常、これには2〜4の値が使用されます。

最後に、異常値を検出する方法を使用して、百分位数を使用できます。値の特定の割合は、上または下から外れ値と見なすことができます。同様に、外れ値の境界として使用される百分位数の値は、データの分布によって異なります。これは、PalmerPenguinsデータセットで実行できる操作です。

upper_lim = data['culmen_length_mm'].quantile(.95)
lower_lim = data['culmen_length_mm'].quantile(.05)
 
no_outliers = data[(data['culmen_length_mm']< upper_lim)&(data['culmen_length_mm']> lower_lim)]
no_outliers

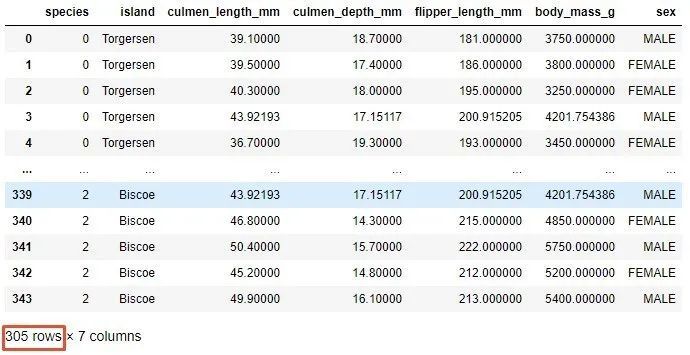
この操作の完了後、データセットには305個のサンプルがあります。この方法を使用する場合、データセットのサイズが小さくなり、データの分散に大きく依存するため、十分に注意する必要があります。

4. スプリットボックス

ビニングは、さまざまな値をビンにグループ化できる簡単な手法です。たとえば、次のような数値の特徴を分類する場合：

この場合、デジタル機能をカテゴリ機能に置き換えます。

ただし、分類値も分類できます。たとえば、国/地域を大陸ごとに分類できます。

ビニングの問題は、パフォーマンスが低下する可能性があることですが、オーバーフィットを防ぎ、機械学習モデルの堅牢性を向上させることができます。コードでは次のようになります。

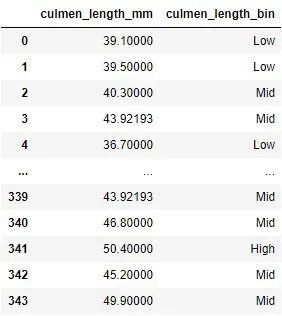
bin_data = data[['culmen_length_mm']]
bin_data['culmen_length_bin']= pd.cut(data['culmen_length_mm'], bins=[0,40,50,100], \
          labels=["Low","Mid","High"])
bin_data

5. ズーム

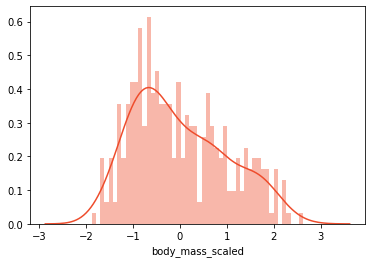
以前の記事では、スケーリングが機械学習モデルがより良い予測を行うのにどのように役立つかを学ぶ機会がしばしばあります。スケーリングの理由は単純です。機能が同じ範囲にない場合、機械学習アルゴリズムはそれらを異なる方法で処理します。つまり、値の範囲が0〜10の機能と、値の範囲が0〜100の別の機能がある場合、機械学習アルゴリズムは、2番目の機能が最初の機能よりも多いと推測する可能性があります。値が高いため重要です。これが常に当てはまるとは限らないことはすでにわかっています。一方、実際のデータが同じ範囲にあると期待するのは非現実的です。これが、スケールを使用して数値特徴を同じ範囲に配置する理由です。この標準化されたデータは、多くの機械学習アルゴリズムの一般的な要件です。それらのいくつかは、関数が標準の通常分散データのように見えることさえ要求します。データはさまざまな方法でスケーリングおよび正規化できますが、データを調べる前に、PalmerPenguinsデータセット「body_mass_g」の機能を見てみましょう。

scaled_data = data[['body_mass_g']]print('Mean:', scaled_data['body_mass_g'].mean())print('Standard Deviation:', scaled_data['body_mass_g'].std())

さらに、この機能の配布に注意してください。

まず、分布を維持するスケーリング手法を検討します。

5.1 標準ズーム

このタイプのスケーリングでは、平均およびスケーリングデータが単位分散として削除されます。これは、次の式で定義されます。

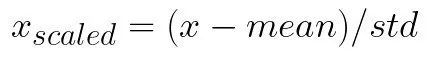
平均はトレーニングサンプルの平均であり、stdはトレーニングサンプルの標準偏差です。それを理解する最良の方法は、実際にそれを観察することです。これには、SciKitLearnクラスとStandardScalerクラスを使用します。

standard_scaler =StandardScaler()
scaled_data['body_mass_scaled']= standard_scaler.fit_transform(scaled_data[['body_mass_g']])print('Mean:', scaled_data['body_mass_scaled'].mean())print('Standard Deviation:', scaled_data['body_mass_scaled'].std())

元のデータ分布が保持されていることがわかります。ただし、データは現在-3から3の間です。

5.2 最小-最大ズーム比（正規化）

最も一般的なスケーリング手法は正規化です（最小-最大正規化および最小-最大スケーリングとも呼ばれます）。 0から1の範囲ですべてのデータをスケーリングします。この手法は、次の式で定義されます。

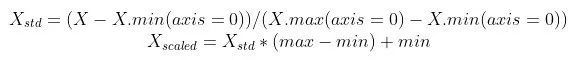
SciKit学習ライブラリでMinMaxScalerを使用する場合：

minmax_scaler =MinMaxScaler()
scaled_data['body_mass_min_max_scaled']= minmax_scaler.fit_transform(scaled_data[['body_mass_g']])print('Mean:', scaled_data['body_mass_min_max_scaled'].mean())print('Standard Deviation:', scaled_data['body_mass_min_max_scaled'].std())

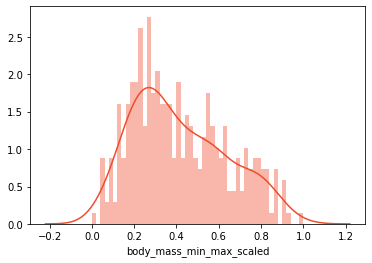
割り当ては予約されていますが、データは0から1の範囲になっています。

5.3 量子変換

前述のように、機械学習アルゴリズムでは、データの分散が均一または正常である必要がある場合があります。これを実現するには、SciKitLearnのQuantileTransformerクラスを使用できます。まず、これは、データが均一な分布に変換されたときの様子です。

qtrans =QuantileTransformer()
scaled_data['body_mass_q_trans_uniform']= qtrans.fit_transform(scaled_data[['body_mass_g']])print('Mean:', scaled_data['body_mass_q_trans_uniform'].mean())print('Standard Deviation:', scaled_data['body_mass_q_trans_uniform'].std())

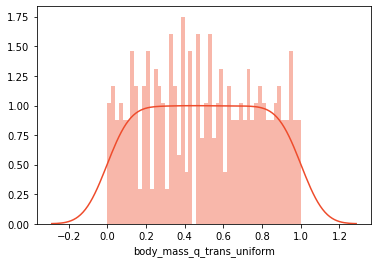
これは、データを通常の分布にするためのコードです。

qtrans =QuantileTransformer(output_distribution='normal', random_state=0)
scaled_data['body_mass_q_trans_normal']= qtrans.fit_transform(scaled_data[['body_mass_g']])print('Mean:', scaled_data['body_mass_q_trans_normal'].mean())print('Standard Deviation:', scaled_data['body_mass_q_trans_normal'].std())

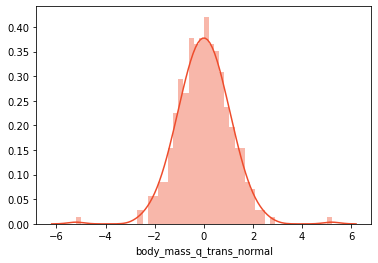
基本的に、output_distributionパラメーターは、ディストリビューションタイプを定義するためにコンストラクターで使用されます。最後に、すべての機能のズーム値を観察し、さまざまなズームタイプを使用できます。

6. ログ変換

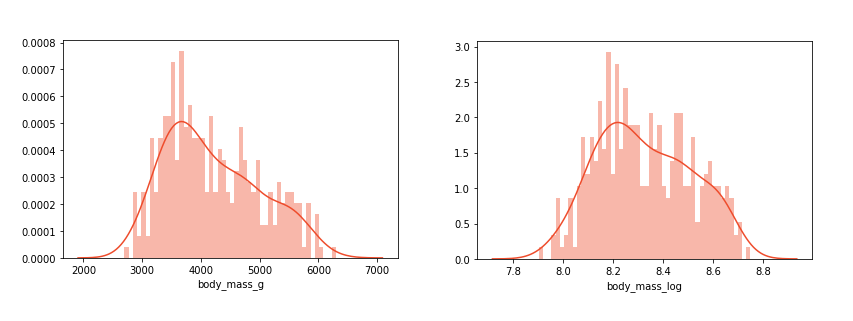
対数変換は、データの最も一般的な数学的変換の1つです。基本的に、ログ機能を現在の値に適用するだけです。データは正でなければならないことに注意することが重要です。そのため、事前にデータをスケーリングまたは正規化する必要がある場合。このシフトは多くの利点をもたらします。その1つは、データの分散がより正常になったことです。これにより、偏ったデータを処理し、異常値の影響を減らすことができます。コードでは次のようになります。

log_data = data[['body_mass_g']]
log_data['body_mass_log']=(data['body_mass_g']+1).transform(np.log)
log_data

変換されていないデータと変換されたデータの分布を確認すると、変換されたデータが通常の分布に近いことがわかります。

7. 機能選択

クライアントからのデータセットは通常非常に大きいです。数百または数千もの機能を持つことができます。特に特定のテクニックが上から実行される場合。多数の機能がオーバーフィットにつながる可能性があります。さらに、一般に、ハイパーパラメータとトレーニングアルゴリズムの最適化には時間がかかります。これが、最も関連性の高い機能を最初から選択する必要がある理由です。

機能の選択に関しては、いくつかの手法がありますが、このチュートリアルでは、最も単純な（そして最も一般的に使用される）1変量機能の選択のみを紹介します。この方法は、単変量統計テストに基づいています。統計テスト（χ2など）を使用して、出力フィーチャがデータセット内の各フィーチャにどの程度依存しているかを計算します。この例では、SelectKBestが使用されています。これには、統計テストを使用するときに複数のオプションがあります（ただし、デフォルト値は、この例で使用されるχ2です）。これを行うことができます：

feature_sel_data = data.drop(['species'], axis=1)
 
feature_sel_data["island"]= feature_sel_data["island"].cat.codes
feature_sel_data["sex"]= feature_sel_data["sex"].cat.codes
 
# Use 3 features
selector =SelectKBest(f_classif, k=3)
 
selected_data = selector.fit_transform(feature_sel_data, data['species'])
selected_data
array([[39.1,18.7,181.],[39.5,17.4,186.],[40.3,18.,195.],...,[50.4,15.7,222.],[45.2,14.8,212.],[49.9,16.1,213.]])

ハイパーパラメータkを使用して、データセットで最も影響力のある3つの機能が定義されます。この操作の出力は、選択した要素を含むNumPy配列です。パンダデータフレームに配置するには、次の手順を実行する必要があります。

selected_features = pd.DataFrame(selector.inverse_transform(selected_data),
         index=data.index,
         columns=feature_sel_data.columns)
 
selected_columns = selected_features.columns[selected_features.var()!=0]
selected_features[selected_columns].head()

8. 機能のグループ化

これまでのところ、いわゆる「クリーンさ」の観点から、観測されたデータセットはほぼ完璧です。つまり、各要素には独自の列があり、各観測値は行であり、各タイプの観測単位はテーブルです。ただし、観測値が複数の行に分散している場合があります。機能グループ化の目的は、これらの行を1つの行に接続してから、これらの要約された行を使用することです。これを行う際の主な問題は、どの集計機能が機能に適用されるかです。これは、分類機能の場合は特に複雑です。

前述のように、PalmerPenguinsデータセットは非常に一般的であるため、次の例は、この操作に使用できるコードを説明するためにのみ使用されています。

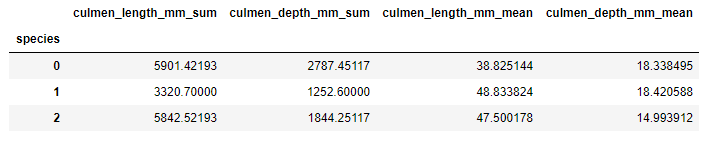
grouped_data = data.groupby('species')
 
sums_data = grouped_data['culmen_length_mm','culmen_depth_mm'].sum().add_suffix('_sum')
avgs_data = grouped_data['culmen_length_mm','culmen_depth_mm'].mean().add_suffix('_mean')
 
sumed_averaged = pd.concat([sums_data, avgs_data], axis=1)
sumed_averaged

ここでは、データがスパイス値ごとにグループ化され、値ごとに合計値と平均値を持つ2つの新しい機能が作成されます。

9. 機能分割

データが行間ではなく列間で接続されている場合があります。たとえば、関数の1つに名前のリストがあるとします。

data.names

0 Andjela Zivkovic

1 Vanja Zivkovic

2 Petar Zivkovic

3 Veljko Zivkovic

4 Nikola Zivkovic

したがって、この関数から名前を抽出するだけの場合は、次のようにすることができます。

data.names

0 Andjela

1 Vanja

2 Petar

3 Veljko

4 Nikola

この手法は機能セグメンテーションと呼ばれ、通常は文字列データに使用されます。

結論として

この記事では、最も一般的に使用される9つの機能エンジニアリング手法を探求する機会があります。

Recommended Posts

Pythonの9つの機能エンジニアリング手法
Python3.9の7つの機能
Pythonで実装された特徴抽出操作の例
Python構文の基本
Pythonの基本構文
Pythonの基礎知識（1）
pythonのPrettytableモジュール
09.Python3の共通モジュール
Pythonの基盤を統合する（4）
Python（7）の基盤を統合する
pythonリスト（LIST）の深い理解
Pythonのタプルの添え字
wavファイルのPython分析
Python（6）の基盤を統合する
栄光のパイソンキング壁紙
Python（5）の基盤を統合する
Pythonサンドボックスエスケープの分析
Python3.10のいくつかの新機能
Pythonマルチスレッドの深い理解
Pythonオブジェクト指向プログラミングの分析
OpenCVインストールのPythonバージョン
python描画モジュールのmatplotlib
パラメータを渡すPythonメソッド
Pythonの基盤を統合する（3）
Python共通モジュールのコレクション
pythonでのwheelの使用法
Pythonの対数法の要約
pythonバックトラッキングテンプレートの詳細な説明
Pythonイールドの使用例の分析
Python開発でのパンダの使用
Pythonプラグインメカニズムの詳細な実装
pythonシーケンスタイプの詳細な説明
pythonリストの逆トラバーサルの実装
IOU計算ケースのPython実装
Python変数スコープの詳細な理解
word2vec操作のPython予備実装
情報エントロピーの例のPython計算
pythonselenium操作cookieの実装
Python開発でのnumpyの使用
地主取引のPythonシミュレーション
Pythonの用途は何ですか
Pythonクローラーのスクレイピーシミュレーションログイン
Python条件付き制御ステートメントの分析
Python1のブラックハットプログラミングアプリケーション
pythonでのosパッケージの使用
Python関数のいくつかの一般的なモード
200のPython標準ライブラリの要約！
pythonクローラーのMongodbとpythonの相互作用
python3登録グローバルホットキーの実装
python学生管理システムの実装
pythonにはいくつかのバージョンがあります
python操作redisのいくつかの例
Pythonモジュールの知識の完全な分析
pythonアクセスAlipayの操作例
Python文字列プーリングの前提
Python3.8の新機能の秘密
python勾配降下アルゴリズムの実装
パイソンクローラー開発の学習パス
Pythonの父がMicrosoftに加わる
Pythonは写真の水平ステッチを実装しています
python accesshdfsの操作