情報エントロピーの例のPython計算

情報エントロピーの計算式：nはカテゴリの数、p（xi）はi番目のカテゴリの確率です。

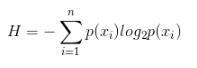
データセットにm行、つまりmサンプルがあり、各行の最後の列がサンプルのラベルであるとすると、データセットの情報エントロピーを計算するためのコードは次のようになります。

from math import log
 
def calcShannonEnt(dataSet):
 numEntries =len(dataSet) #サンプル数
 labelCounts ={} #データセット内の各カテゴリの頻度
 for featVec in dataSet: #各行のサンプル
 currentLabel = featVec[-1] #サンプルのラベル
 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel]=0
 labelCounts[currentLabel]+=1 
 shannonEnt =0.0for key in labelCounts:
 prob =float(labelCounts[key])/numEntries #pを計算する(xi)
 shannonEnt -= prob *log(prob,2) # log base 2return shannonEnt

補足知識：pythonは、情報エントロピー、条件付きエントロピー、情報ゲイン、Gini係数を実現します

ナンセンスなことはあまり言いませんが、みんなコードを見てください〜

import pandas as pd
import numpy as np
import math
## 情報エントロピーを計算する
def getEntropy(s):
 # 異なる値の出現数を見つける
 if not isinstance(s, pd.core.series.Series):
 s = pd.Series(s)
 prt_ary = pd.groupby(s , by = s).count().values /float(len(s))return-(np.log2(prt_ary)* prt_ary).sum()
## 条件付きエントロピーを計算する:条件s1でのs2の条件付きエントロピー
def getCondEntropy(s1 , s2):
 d =dict()for i inlist(range(len(s1))):
 d[s1[i]]= d.get(s1[i],[])+[s2[i]]returnsum([getEntropy(d[k])*len(d[k])/float(len(s1))for k in d])

## 情報ゲインを計算する
def getEntropyGain(s1, s2):returngetEntropy(s2)-getCondEntropy(s1, s2)

## ゲインレートを計算する
def getEntropyGainRadio(s1, s2):returngetEntropyGain(s1, s2)/getEntropy(s2)

## 離散値の相関を測定する
import math
def getDiscreteCorr(s1, s2):returngetEntropyGain(s1,s2)/ math.sqrt(getEntropy(s1)*getEntropy(s2))

# ######## 二乗の確率和を計算する
def getProbSS(s):if not isinstance(s, pd.core.series.Series):
 s = pd.Series(s)
 prt_ary = pd.groupby(s, by = s).count().values /float(len(s))returnsum(prt_ary **2)
######## ジニ係数を計算する
def getGini(s1, s2):
 d =dict()for i inlist(range(len(s1))):
 d[s1[i]]= d.get(s1[i],[])+[s2[i]]return1-sum([getProbSS(d[k])*len(d[k])/float(len(s1))for k in d])
## 離散変数の相関係数を計算し、ヒートマップを作成します,相関行列を返します
def DiscreteCorr(C_data):
 ## 離散変数の場合(C_data)相関係数を計算する
 C_data_column_names = C_data.columns.tolist()
 ## ストアC_データ相関係数のマトリックス
 import numpy as np
 dp_corr_mat = np.zeros([len(C_data_column_names),len(C_data_column_names)])for i inrange(len(C_data_column_names)):for j inrange(len(C_data_column_names)):
  # 2つの属性間の相関係数を計算します
  temp_corr =getDiscreteCorr(C_data.iloc[:,i], C_data.iloc[:,j])
  dp_corr_mat[i][j]= temp_corr
 # 相関係数グラフを描く
 fig = plt.figure()
 fig.add_subplot(2,2,1)
 sns.heatmap(dp_corr_mat ,vmin=-1, vmax=1, cmap= sns.color_palette('RdBu', n_colors=128), xticklabels= C_data_column_names , yticklabels= C_data_column_names)return pd.DataFrame(dp_corr_mat)if __name__ =="__main__":
 s1 = pd.Series(['X1','X1','X2','X2','X2','X2'])
 s2 = pd.Series(['Y1','Y1','Y1','Y2','Y2','Y2'])print('CondEntropy:',getCondEntropy(s1, s2))print('EntropyGain:',getEntropyGain(s1, s2))print('EntropyGainRadio',getEntropyGainRadio(s1 , s2))print('DiscreteCorr:',getDiscreteCorr(s1, s1))print('Gini',getGini(s1, s2))

上記のPythonでの情報エントロピーの計算例は、エディターが共有するすべてのコンテンツです。参考にしてください。