pythonは勾配メソッドを実装しますpython最速の降下メソッド

勾配法の原理、つまり最も急な降下法をすでに知っていると仮定します。

次に例を挙げます。

手動で直接解決する場合：

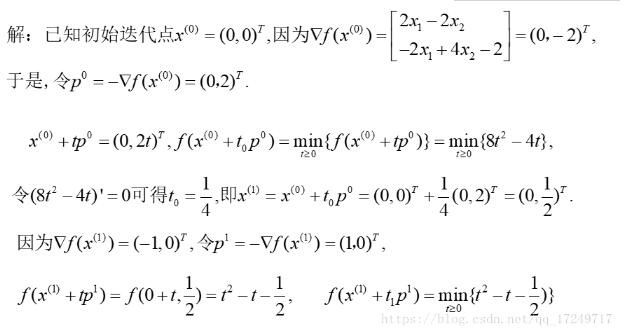
次に、Pythonソリューションプロセスを示します。

import numpy as np
from sympy import*import math
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist

# 定義記号
x1, x2, t =symbols('x1, x2, t')

def func():
 # 機能をカスタマイズする
 returnpow(x1,2)+2*pow(x2,2)-2* x1 * x2 -2* x2

def grad(data):
 # 勾配ベクトルを見つける,data=[data1, data2]
 f =func()
 grad_vec =[diff(f, x1),diff(f, x2)] #部分導関数を見つける,勾配ベクトル
 grad =[]for item in grad_vec:
 grad.append(item.subs(x1, data[0]).subs(x2, data[1]))return grad

def grad_len(grad):
 # 勾配ベクトルのモジュラス長
 vec_len = math.sqrt(pow(grad[0],2)+pow(grad[1],2))return vec_len

def zhudian(f):
 # 分を見つける(t)停滞点
 t_diff =diff(f)
 t_min =solve(t_diff)return t_min

def main(X0, theta):
 f =func()
 grad_vec =grad(X0)
 grad_length =grad_len(grad_vec) #勾配ベクトルのモジュラス長
 k =0
 data_x =[0]
 data_y =[0]while grad_length   theta: #反復の終了条件
 k +=1
 p =-np.array(grad_vec)
 # 反復
 X = np.array(X0)+ t*p
 t_func = f.subs(x1, X[0]).subs(x2, X[1])
 t_min =zhudian(t_func)
 X0 = np.array(X0)+ t_min*p
 grad_vec =grad(X0)
 grad_length =grad_len(grad_vec)print('grad_length', grad_length)print('座標', X0[0], X0[1])
 data_x.append(X0[0])
 data_y.append(X0[1])print(k)

 # 図
 fig = plt.figure()
 ax = axisartist.Subplot(fig,111)
 fig.add_axes(ax)
 ax.axis["bottom"].set_axisline_style("-| ", size=1.5)
 ax.axis["left"].set_axisline_style("- ", size=1.5)
 ax.axis["top"].set_visible(False)
 ax.axis["right"].set_visible(False)
 plt.title(r'$Gradient \ method - steepest \ descent \ method$')
 plt.plot(data_x, data_y, label=r'$f(x_1,x_2)=x_1^2+2 \cdot x_2^2-2 \cdot x_1 \cdot x_2-2 \cdot x_2$')
 plt.legend()
 plt.scatter(1,1, marker=(5,1), c=5, s=1000)
 plt.grid()
 plt.xlabel(r'$x_1$', fontsize=20)
 plt.ylabel(r'$x_2$', fontsize=20)
 plt.show()if __name__ =='__main__':
 # 与えられた初期反復ポイントとしきい値
 main([0,0],0.00001)

最終結果を以下に示します。

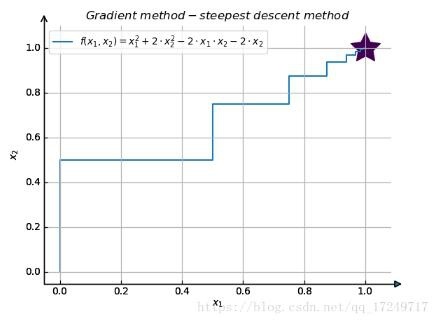
以上が本稿の内容ですので、皆様のご勉強に役立てていただければ幸いです。