Pythonは勾配降下法を実装しています
この記事の例では、参照用に勾配降下法を実装するためのpythonの特定のコードを共有しています。具体的な内容は次のとおりです。
使用ツール: Python(x、y)2.6.6
動作環境: Windows10
問題:y = 2 * x1 + x2 + 3を解きます。つまり、勾配降下法を使用して、y = a * x1 + b * x2 + c(監視学習)のパラメーターa、b、cの最適値を解きます。
トレーニングデータ:
x_train=[1, 2], [2, 1],[2, 3], [3, 5], [1,3], [4, 2], [7, 3], [4, 5], [11, 3], [8, 7]
y_train=[7, 8, 10, 14, 8, 13, 20, 16, 28,26]
テストデータ:
x_test = [1, 4],[2, 2],[2, 5],[5, 3],[1,5],[4, 1]
# - *- coding: utf-8-*-"""
Created on Wed Nov 1609:37:032016
@ author: Jason
"""
import numpy as np
import matplotlib.pyplot as plt
# y=2*(x1)+(x2)+3
rate =0.001
x_train = np.array([[1,2],[2,1],[2,3],[3,5],[1,3],[4,2],[7,3],[4,5],[11,3],[8,7]])
y_train = np.array([7,8,10,14,8,13,20,16,28,26])
x_test = np.array([[1,4],[2,2],[2,5],[5,3],[1,5],[4,1]])
a = np.random.normal()
b = np.random.normal()
c = np.random.normal()
def h(x):return a*x[0]+b*x[1]+c
for i inrange(100):
sum_a=0
sum_b=0
sum_c=0for x, y inzip(x_train, y_train):for xi in x:
sum_a = sum_a+ rate*(y-h(x))*xi
sum_b = sum_b+ rate*(y-h(x))*xi
# sum_c = sum_c + rate*(y-h(x))*1
a = a + sum_a
b = b + sum_b
c = c + sum_c
plt.plot([h(xi)for xi in x_test])print(a)print(b)print(c)
result=[h(xi)for xi in x_train]print(result)
result=[h(xi)for xi in x_test]print(result)
plt.show()
動作結果:
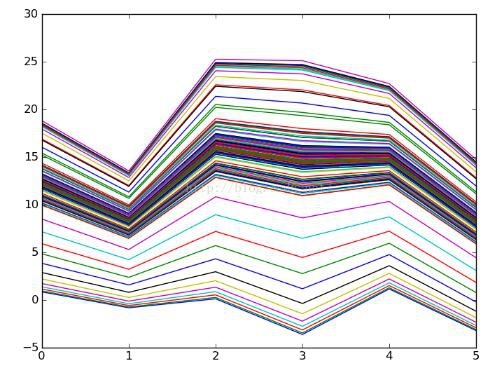
**結論:**ラインセグメントは徐々に近づいています。トレーニングデータと反復が多いほど、真の値に近づきます。
以上が本稿の内容ですので、皆様のご勉強に役立てていただければ幸いです。
Recommended Posts