Pythonデータサイエンス：Chi-Square Test

以前に導入された変数の分析：

①相関分析：連続変数と連続変数の関係。

②** 2サンプルtテスト**：二分されたカテゴリー変数と連続変数の関係。

③分散の分析：マルチカテゴリカテゴリ変数と連続変数の関係。

この紹介：

**Chi-square test **：二分されたカテゴリー変数またはマルチクラスのカテゴリー変数と二分されたカテゴリー変数の間の関係。

一方の変数の分布がもう一方の変数のレベルによって変化する場合、2つのカテゴリ変数は関連しています。

カイ二乗検定では、2つのカテゴリ変数間の相関の強さを示すことはできませんが、2つのカテゴリ変数が関連しているかどうかのみを示すことができます。

/ 01 /データマイニングの技術と方法

データマイニング方法は、記述的方法と予測的方法の2つのタイプに分けられます。

どちらの方法も、分析用の履歴データに基づいています。

記述モデルは、過去の状況を直接反映し、その後の分析にインスピレーションを与えるために使用されます。

予測モデルは、履歴データからパターンを見つけ、それらを使用して将来を予測します。

記述的データマイニングの一般的なアルゴリズム：クラスター分析、アソシエーションルール分析。

予測データマイニングに一般的に使用されるアルゴリズム：線形回帰、ロジスティック回帰、ニューラルネットワーク、決定ツリー、サポートベクターマシン。

/ 02 /カイスクエアテスト

01 不測の事態の表

不測の事態のテーブルは一種の要約テーブルです。

分析する2つのカテゴリ変数のいずれかの各カテゴリを列変数として設定します。

他の変数の各カテゴリは行変数として設定され、中央は異なるカテゴリの頻度に対応します。

この本のデータを例として取り上げて、カテゴリ変数がデフォルトであるかどうかと、カテゴリ変数が破産しているかどうかの関係を調べてみましょう。

使用するデータは、原文を読むことで取得できます。

import pandas as pd

df = pd.read_csv('accepts.csv')
# crosstab:クロステーブル,margins:合計を表示
cross_table = pd.crosstab(df['bankruptcy_ind'], df['bad_ind'], margins=True)print(cross_table)

結果を出力します。

ここで関係を判断するのは簡単ではないので、以下の周波数に変換してみましょう。

# div:リストを周波数データに変換する
cross_table_last = cross_table.div(cross_table['All'], axis=0)print(cross_table_last)

結果を出力します。

違いはそれほど大きくないことがわかりますが、直接結論を出すことはできません。

破産が契約違反の有無と関係がないかどうかは、より大きな可能性があるとしか言えません。

次に、カイ二乗検定を使用して結論を決定し、統計的に有意にします。

02 カイスクエアテスト

カイ二乗テストは、予想される周波数と実際の周波数の間の一致の程度を比較することです。

実際の頻度はセル内の実際の観測数であり、実際の頻度の分母はサンプルの総数です。

期待周波数は、変数が互いに独立している場合の周波数であり、期待周波数によって計算され、期待周波数は実際の周波数から導出されます。

カイ二乗検定のヌル仮説は、期待される頻度が実際の頻度に等しいということです。つまり、2つのカテゴリ変数は無関係であり、代替の仮説は関連しています。

カイ二乗統計は式によって計算され、その値はカイ二乗分布に従います。

カイ二乗分布図は次のとおりです。横軸はカイ二乗統計値、縦軸はP値、nは自由度です。

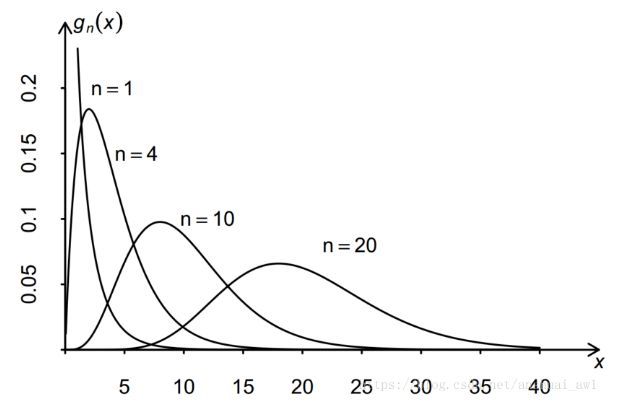
この場合、個人的には自由度は1だと思います。なぜ自由度は2と書いてあるのでしょうか。 ？ ？

Pythonを使用して、データに対してカイスクエアテストを実行してみましょう。

from scipy import stats

# chi2_contingency:カイスクエアテスト,chisq:カイ二乗統計値,expected_freq:予想される頻度
print('chisq = %6.4f\n p-value = %6.4f\n dof = %i\n expected_freq = %s'%stats.chi2_contingency(cross_table))

結果を出力します。

カイ二乗値は2.9167、P値は0.5719、有意水準は0.05であり、ヌル仮説を棄却する理由がないことを示しています。

つまり、2つのカテゴリ変数は無関係であり、契約違反があるかどうかは、それが破産しているかどうかとは関係ありません。

/ 03 /まとめ

これが自由度に関する知識の要約です。

メカニックとして、私には6つの自由度しかないはずです。

X、Y、Z軸の3つの回転と3つの動き。

しかし、これは統計には当てはまりません。

①自由度とは、サンプルの統計量から全体のパラメータを推定した場合の、サンプル内の独立したデータまたは自由に変化するデータの数を指します。

②自由度とは、独立して変更できるデータの数です。n-1の数が決まっている限り、nの数が決まっていて、自由に変更することはできません。

正直に言うと...