Pythonデータサイエンス:線形回帰診断
前回の線形回帰の記事に続いて、ポータルは次のようになります。
[ Python Data Science:Linear Regression](http://mp.weixin.qq.com/s?__biz=MzU4OTYzNjE2OQ==&mid=2247484227&idx=1&sn=4e383b99c85c46841cc65c4f5b298d30&chksm=fdcb3465cabc85e
多重線形回帰の前提条件:
- 従属変数は、外乱項と線形関係を持つことはできません
- 独立変数と従属変数の間には線形関係がなければなりません
- 独立変数間に強すぎる線形関係があってはなりません
- 外乱項または残差は独立しており、平均が0で一定の分散を持つ正規分布に従う必要があります。
/ 01 /残留エラー分析
残留エラー分析は、線形回帰診断の重要な部分です。
残差が従う必要がある3つの前提条件があります。
- 残差分散の均一性
- 残差は独立しており、同じように分散されます
- 残差を独立変数と相関させることはできません(テストできません)
残差グラフを表示して残差を確認します。
残差グラフは、次の4つのカテゴリに分類できます。
- 残差は通常分布しています。残差はランダムに分布しており、上限と下限は基本的に対称であり、明らかな自己相関はなく、分散は基本的に均一です。
- 残差曲線分布:残差と予測値は曲線関係にあり、独立変数と従属変数が線形ではないことを示しています
- 不均一な残差分散:残差の上限と下限は基本的に対称ですが、予測値が増加すると、上限と下限の範囲も増加します
- 残差誤差の周期的変化:予測値の増加に伴い残差誤差が周期的に変化し、独立変数と従属変数が周期的に変化する可能性があることを示しています。
例として、前の線形回帰の記事のモデルを取り上げましょう。
# 単純な線形回帰モデル,平均支出と収入
ana1 = lm_s
# トレーニングデータセットの予測値
exp['Pred']= ana1.predict(exp)
# トレーニングデータセットの残差
exp['resid']= ana1.resid
# 収入と残差の分散プロットを描く
exp.plot('Income','resid', kind='scatter')
plt.show()
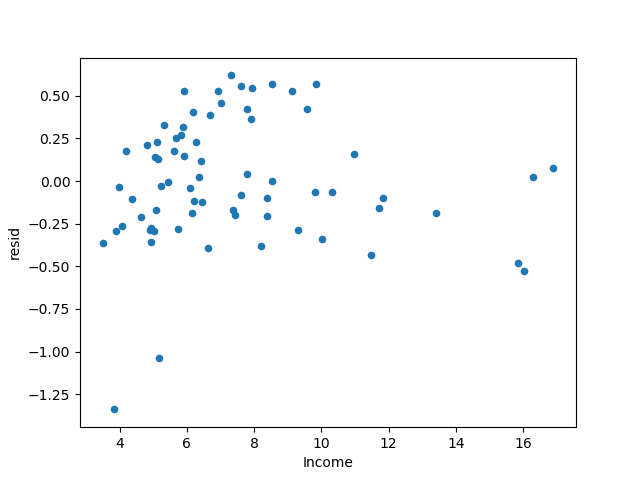
モデルの残差が得られます。予測値が増加しても、残差は基本的に対称のままです。
ただし、正と負の残差の大きさは徐々に大きくなる傾向があります。つまり、モデルには不均一な分散の問題があります。

異質性の処理方法は対数でデータを取得できるため、ここでは平均支出データを対数で処理します。
# 単純な線形回帰を使用してモデルを構築する,平均支出データをログに記録する
ana2 =ols('avg_exp_ln ~ Income', data=exp).fit()
exp['Pred']= ana2.predict(exp)
# トレーニングデータセットの残差
exp['resid']= ana2.resid
# 収入と残差の分散プロットを描く
exp.plot('Income','resid', kind='scatter')
plt.show()
モデルの残差を取得し、正と負の残差の大きさが改善する傾向があることを確認します。
本は異質性現象が改善されたと言っていますが、私はそれがかなり良いと感じています...
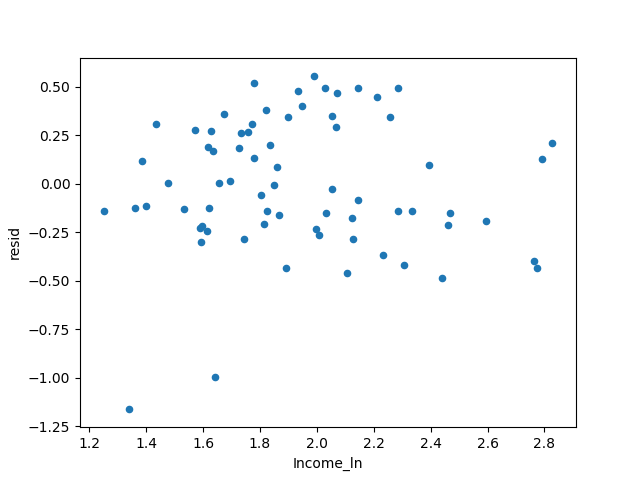
上記は平均支出データの対数のみを取り、以下は収入データの対数を取りますので、2つの増加率はほぼ同じです。
# 所得データの対数,np.log(e)=1
exp['Income_ln']= np.log(exp['Income'])
# 単純な線形回帰を使用してモデルを構築する,平均支出データをログに記録する
ana3 =ols('avg_exp_ln ~ Income_ln', data=exp).fit()
exp['Pred']= ana3.predict(exp)
# トレーニングデータセットの残差
exp['resid']= ana3.resid
# 収入と残差の分散プロットを描く
exp.plot('Income_ln','resid', kind='scatter')
plt.show()
この本には、異質性現象が解消されたと書かれています。前の写真と大きな違いは見られません...
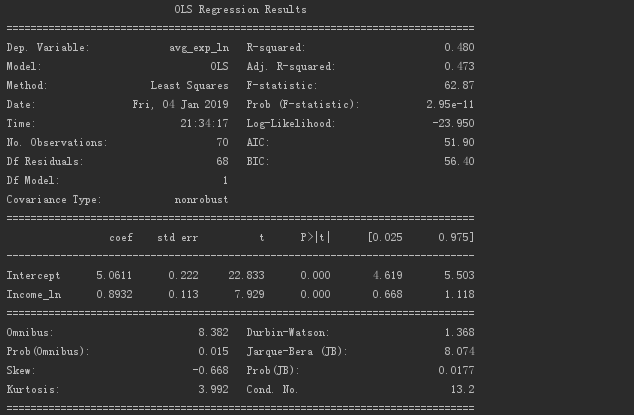
3つのモデルのR²の状況を比較します。
# 3つのモデルのR²値を取得します
r_sq ={'exp~Income': ana1.rsquared,'ln(exp)~Income': ana2.rsquared,'ln(exp)~ln(Income)': ana3.rsquared}print(r_sq)
# 出力結果
{' ln(exp)~Income':0.4030855555329649,'ln(exp)~ln(Income)':0.480392799389311,'exp~Income':0.45429062315565294}
対数モデルのR²が最大であり、モデルは3つの中で最も優れていると見なされていることがわかります。
DWテスト(ダービン-ワトソンテスト)は、残差の自己相関関係を判断するために使用できます。
DW値が2に近づくと、残差には自己相関関係がないと見なすことができます。
以下は、対数モデルによって出力される判断指標です。
対数を取るすべてのモデルのDW値は1.368であることがわかります。
相関関係が何であるかわかりません、それは正の相関関係かもしれません...
/ 02 /強い影響力
ポイントがグループから離れすぎている場合、フィットされた回帰線はこのポイントによって強く乱され、それによって回帰線の位置が変更されます。
これが強い影響力のポイントです。
ここでは、予測値を学習した残差マップを使用して、強い影響ポイントを特定できます。
学生化残差(SR)は、標準化された残差を指します。
# 学生化された残差計算
exp['resid_t']=(exp['resid']- exp['resid'].mean())/ exp['resid'].std()
# サンプルサイズが数百の場合は2を取ります,サンプルサイズが数千の場合は3枚撮ります(exp[abs(exp['resid_t'])>2])
出力は次のとおりです。

全部で2つあります。前のスキャッタープロットから、誰もが2つのポイントがどれであるかを知ることができるはずです。
回帰モデルは、強い影響点のデータを削除することによって確立されます。
# 単純な線形回帰を使用してモデルを構築する,影響力の強みを取り除く
exp2 = exp[abs(exp['resid_t'])<=2].copy()
ana4 =ols('avg_exp_ln ~ Income_ln', data=exp2).fit()
exp2['Pred']= ana3.predict(exp)
# トレーニングデータセットの残差
exp2['resid']= ana3.resid
# 収入と残差の分散プロットを描く
exp2.plot('Income_ln','resid', kind='scatter')
plt.show()
答えを得た。
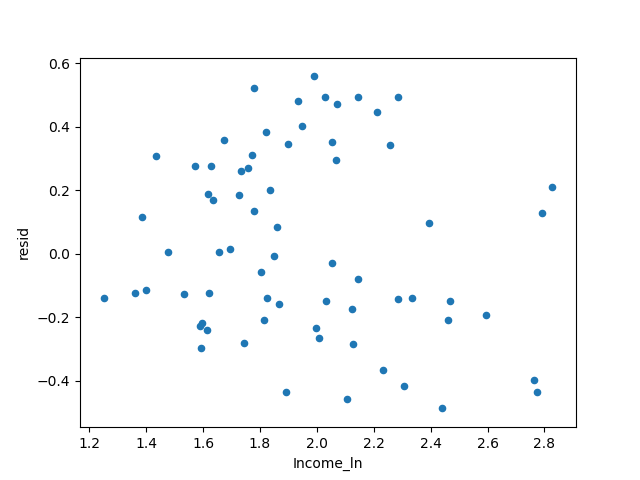
この残差の結果はまだ良好です。
/ 03 /多重共線性分析
マルチ共線性としても知られる、独立変数間に強い共線性はあり得ません。
今回は、分散インフレーション係数を使用して、多重共線性を診断および削減します。
前のデータで、地方の平均住宅価格と地方の平均収入データを追加します。
exp2['dist_home_val_ln']= np.log(exp['dist_home_val'])
exp2['dist_avg_income_ln']= np.log(exp['dist_avg_income'])
def vif(df, col_i):
# 変数を取得する
cols =list(df.columns)
# 従属変数を削除する
cols.remove(col_i)
# 議論を得る
cols_noti = cols
# 多変量線形回帰モデルの確立および取得モデルR²
formula = col_i +'~'+'+'.join(cols_noti)
r2 =ols(formula, df).fit().rsquared
# 分散膨張係数を計算する
return1./(1.- r2)
# 独立変数データを取得する
exog = exp2[['Age','Income_ln','dist_home_val_ln','dist_avg_income_ln']]
# 引数を繰り返します,VIF値を取得する
for i in exog.columns:print(i,'\t',vif(df=exog, col_i=i))
得られた結果。

所得と地方平均所得の間の分散インフレーション係数は10より大きいことがわかり、多重共線性があることを示しています。
この時点で変数の1つを削除する必要があるのは当然のことです。
ここでは、情報をより適切に反映するために、収入データ列の代わりに平均より高い収入の比率が使用されています。
# 平均所得よりも高い割合
exp2['high_avg_ratio']= exp['high_avg']/ exp2['dist_avg_income']
# 独立変数データを取得する
exog2 = exp2[['Age','high_avg_ratio','dist_home_val_ln','dist_avg_income_ln']]
# 引数を繰り返します,VIF値を取得する
for i in exog2.columns:print(i,'\t',vif(df=exog2, col_i=i))
結果を出力します。

各変数の分散展開係数が小さいことがわかり、共線性がないことを示しています。
もちろん、上記の方法では、モデルへの共直線性の干渉を減らすことはできますが、多重共線性を完全に排除することはできません。
/ 04 /まとめ
妥当な線形回帰モデルを構築する手順は次のとおりです。
初期分析:研究目的を決定し、データを収集します。
変数の選択:従属変数に影響を与える独立変数を見つけます。
検証モデルの仮定:
- モデルを設定し、回帰方法を選択し、変数を選択し、どのような形式で変数をモデルに配置するか
- 説明変数と外乱項を相関させることはできません
- 説明変数間に強い線形関係があってはなりません
- 外乱項は独立しており、同じように分布しています
- 外乱アイテムは通常の分布に従います
マルチコリニアリティと強い影響点の診断と分析:修正された回帰モデル。
予測と解釈:モデルを使用して予測と説明を行います。
正直なところ、この部分はわかりにくいです。
ほとんどの場合、私は最初にマークを選択し、次にゆっくりと消化します...
Recommended Posts