Pythonデータサイエンス:正規化方法
前回の線形回帰の記事に続いて、ポータルは次のようになります。
[ Pythonデータサイエンス:線形回帰診断](http://mp.weixin.qq.com/s?__biz=MzU4OTYzNjE2OQ== "mid = 2247484309&idx = 1&sn = 156ca4967d967a164abeab7009faab20&chksm = fdcb34b3cabcbda503c751cdb
上記の記事は、分散インフレーション係数を使用して、線形回帰に対する多重共線性の影響を診断および削減することです。
人間の介入が必要であり(得られた分散インフレーション値に従って判断)、時間がかかりすぎます。
そこで、正規化法の登場があり、収縮法(正規化法)で回帰を行っています。
正規化方法には、主にリッジ回帰とLASSO回帰が含まれます。
/ 01 /リッジリターン
リッジ回帰は、**人為的に追加されたペナルティ項(制約)**を介して回帰係数を推定します。これは、偏った推定です。
偏りのある推定では、推定誤差の大幅な減少と引き換えに、推定にわずかな偏りを持たせることができ、回帰係数は、残差の二乗の最小合計の原理に基づいて推定されます。
通常、リッジ回帰方程式のR²は線形回帰分析よりもわずかに低くなりますが、回帰係数の重要性は通常の線形回帰の重要性よりも大幅に高くなることがよくあります。
対応する理論的知識はここでは詳しく説明されていません。正直なところ、リトルFもめまいがします...
したがって、最初にパッケージを調整して、効果を確認することを選択します。
機械学習フレームワークscikit-learnは、リッジ回帰パラメーター(正規化係数)を選択するために使用されます。
データは本のデータです。ウェブディスクにアップロードされており、公式アカウントから「正規化」と返信して取得します。
scikit-learnのモデルは、デフォルトではデータを標準化していないため、手動で実行する必要があります。
標準化されたデータは次元を排除することができ、各変数の係数を特定の意味で直接比較することができます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.linear_model import RidgeCV
from sklearn.preprocessing import StandardScaler
# パンダの出力の省略記号と改行を削除します
pd.set_option('display.max_columns',500)
pd.set_option('display.width',1000)
# データの読み取り,skipinitialspace:区切り文字の後の空白を無視する
df = pd.read_csv('creditcard_exp.csv', skipinitialspace=True)
# クレジットカードの支出のラインデータを取得する
exp = df[df['avg_exp'].notnull()].copy().iloc[:,2:].drop('age2', axis=1)
# 費用をかけずにクレジットカードの行データを取得する,NaN
exp_new = df[df['avg_exp'].isnull()].copy().iloc[:,2:].drop('age2', axis=1)
# 4つの連続変数を選択します,それぞれ、年齢収入、地域コミュニティの価格、地元の一人当たりの収入
continuous_xcols =['Age','Income','dist_home_val','dist_avg_income']
# 標準化
scaler =StandardScaler()
# 説明変数,二次元配列
X = scaler.fit_transform(exp[continuous_xcols])
# 説明された変数,一次元配列
y = exp['avg_exp_ln']
# 正規化係数を生成する
alphas = np.logspace(-2,3,100, base=10)
# 異なる正規化係数を使用してモデルを相互検証します
rcv =RidgeCV(alphas=alphas, store_cv_values=True)
# データセットトレーニングを使用する(fit)
rcv.fit(X, y)
# 最適なパラメータを出力する,正規化係数と対応するモデルR²
print('The best alpha is {}'.format(rcv.alpha_))print('The r-square is {}'.format(rcv.score(X, y)))
# トレーニング後、データ変換に変換を使用します
X_new = scaler.transform(exp_new[continuous_xcols])
# モデルを使用してデータを予測する
print(np.exp(rcv.predict(X_new)[:5]))
出力は次のとおりです。

最適な正規化係数は0.29で、モデルR²は0.475です。
そして、最適な正規化係数の下でリッジ回帰モデルを使用して、データを予測します。
さまざまな正規化係数の下でのモデルの平均二乗誤差を視覚化します。
# 正規化係数検索スペースでの相互検証の各ラウンドの結果,モデルの平均二乗誤差
cv_values = rcv.cv_values_
n_fold, n_alphas = cv_values.shape
# モデルの平均二乗誤差変動値
cv_mean = cv_values.mean(axis=0)
cv_std = cv_values.std(axis=0)
ub = cv_mean + cv_std / np.sqrt(n_fold)
lb = cv_mean - cv_std / np.sqrt(n_fold)
# 線図を描く,x軸は指数形式です
plt.semilogx(alphas, cv_mean, label='mean_score')
# y1(lb)そしてy2(ub)間に記入
plt.fill_between(alphas, lb, ub, alpha=0.2)
plt.xlabel('$\\alpha$')
plt.ylabel('mean squared errors')
plt.legend(loc='best')
plt.show()
出力は次のとおりです。
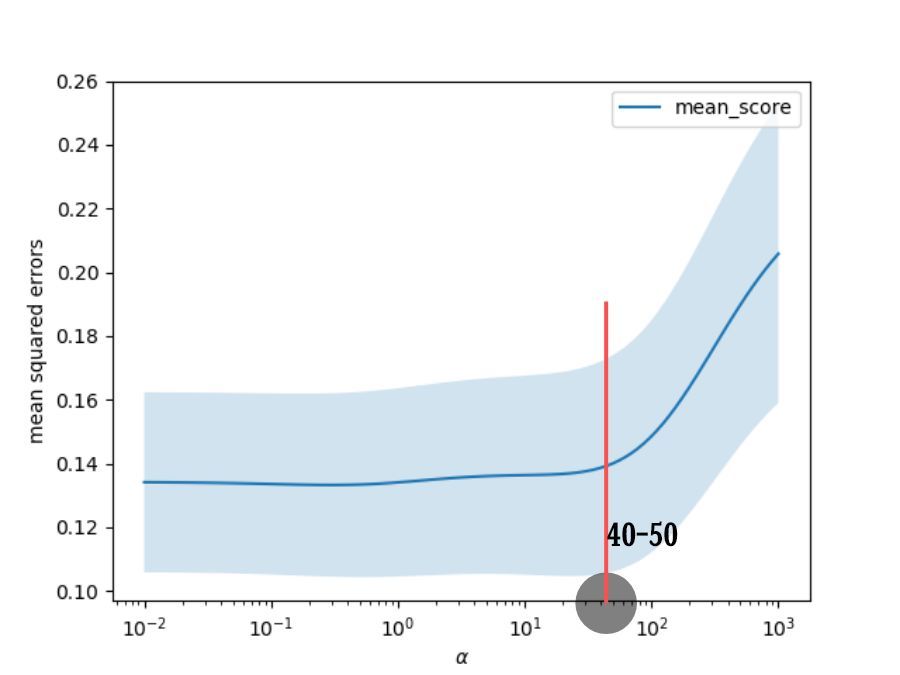
正規化係数が40または50未満の場合、モデルの平均二乗誤差はそれほど変わらないことがわかります。
係数がしきい値を超えると、平均二乗誤差が急激に増加します。
正規化係数が40または50未満である限り、モデルのフィッティング効果は良好であるはずです。
**正規化係数が小さいほど、モデルの適合性は高くなりますが、過剰適合が発生する可能性が高くなります。 ****
**正規化係数が大きいほど、オーバーフィットする可能性は低くなりますが、モデルの偏差は大きくなります。 ****
RidgeCVは、相互検証を通じて「最適な」正規化係数をすばやく返すことができます。
これが数値計算のみに基づいている場合、最終結果はビジネスロジックに準拠しない可能性があります。
たとえば、このモデルの可変係数。
# 出力モデルの可変係数
print(rcv.coef_)
# 出力結果
[0.03321449-0.309561850.055512080.59067449]
収入の係数が負であることに気付くのは間違いなく不合理です。
以下は、尾根トレース図によるさらなる分析です。
尾根トレース図は、さまざまな正規化係数の下での可変係数の軌跡です。
ridge =Ridge()
coefs =[]
# 異なる正規化係数の下での可変係数
for alpha in alphas:
ridge.set_params(alpha=alpha)
ridge.fit(X, y)
coefs.append(ridge.coef_)
# 正規化係数を使用して可変係数の軌道をプロットします
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
結果を出力します。
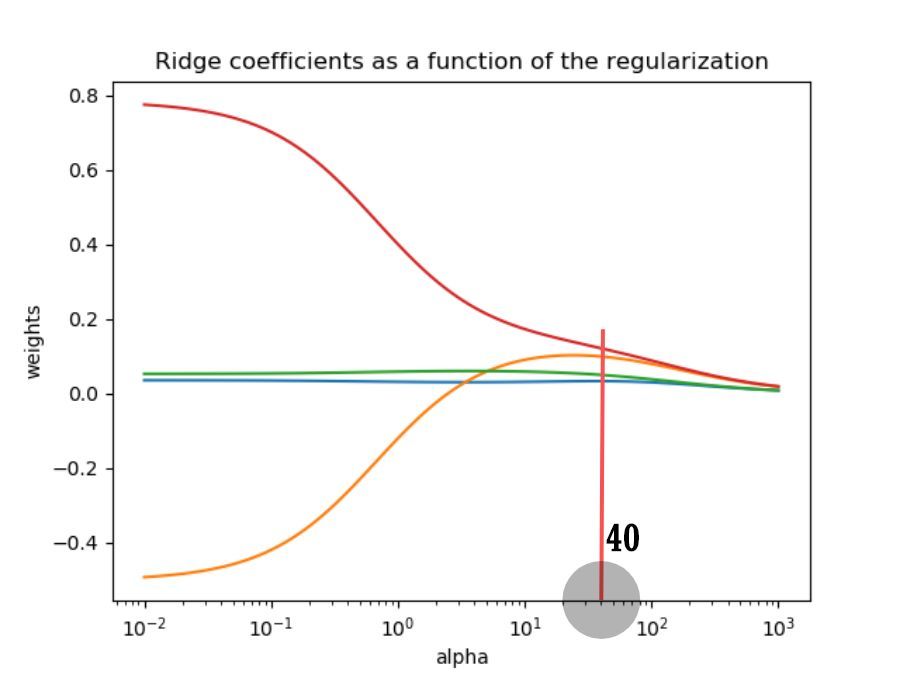
①異なる正規化係数では、2つの変数の係数が0に非常に近いため、削除することを選択できます。
②正規化係数が大きいほど、変数係数のペナルティが大きくなり、すべての変数の係数がゼロになる傾向があります。
③変数の係数の変化が非常に大きく(正と負)、係数の分散が大きく、共線性があることを示しています。
モデルの平均二乗誤差とリッジトレースマップを統合すると、正規化係数は40として選択されます。
**40より大きい場合、モデルの平均二乗誤差が増加し、モデルのフィッティング効果が悪化します。 ****
**40未満の場合、可変係数は不安定になり、共直線性は抑制されません。 ****
次に、正規化係数が40の場合、モデル変数係数を見てみましょう。
ridge.set_params(alpha=40)
ridge.fit(X, y)
# 出力可変係数
print(ridge.coef_)
# 出力モデルR²
print(ridge.score(X, y))
# 予測データ
print(np.exp(ridge.predict(X_new)[:5]))
# 出力結果
[0.032931090.099077470.049763050.12101456]0.4255673043353688[934.79025945727.11042209703.88143602759.04342764709.54172995]
可変係数はすべて正であることがわかり、これはビジネスの直感と一致しています。
所得と一人当たりの地方所得の2つの変数は保持でき、他の2つは削除されます。
/ 02 / LASSOリターン
LASSO回帰は、回帰係数の絶対値の合計が定数よりも小さいという制約条件下で、残差の二乗和を最小化します。
これにより、厳密に0に等しい回帰係数を生成することができ、説明力の強いモデルを得ることができます。
リッジ回帰と比較して、LASSO回帰は変数スクリーニングも実行できます。
LassoCV相互検証を使用して、最適な正規化係数を決定します。
# 正規化係数を生成する
lasso_alphas = np.logspace(-3,0,100, base=10)
# 異なる正規化係数を使用してモデルを相互検証します
lcv =LassoCV(alphas=lasso_alphas, cv=10)
# データセットトレーニングを使用する(fit)
lcv.fit(X, y)
# 最適なパラメータを出力する,正規化係数と対応するモデルR²
print('The best alpha is {}'.format(lcv.alpha_))print('The r-square is {}'.format(lcv.score(X, y)))
# 出力結果
The best alpha is 0.04037017258596556
The r-square is 0.4426451069862233
最適な正規化係数は0.04であり、モデルR²は0.443であることがわかります。
次に、さまざまな正規化係数の下で可変係数の軌跡を取得します。
lasso =Lasso()
lasso_coefs =[]
# 異なる正規化係数の下での可変係数
for alpha in lasso_alphas:
lasso.set_params(alpha=alpha)
lasso.fit(X, y)
lasso_coefs.append(lasso.coef_)
# 正規化係数を使用して可変係数の軌道をプロットします
ax = plt.gca()
ax.plot(lasso_alphas, lasso_coefs)
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Lasso coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
結果を出力します。
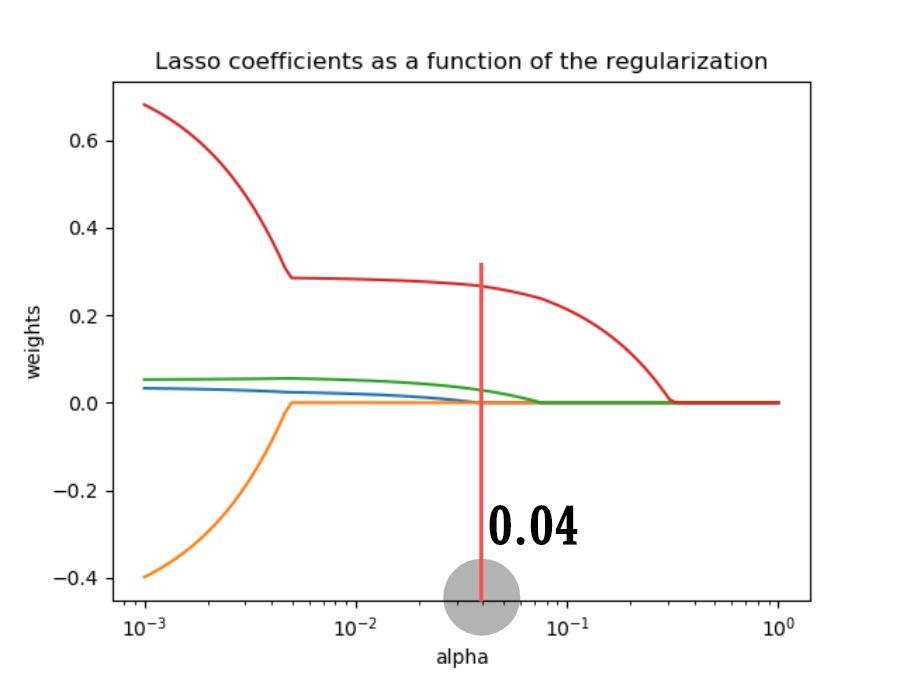
正規化係数が増加すると、すべての変数の係数が特定のしきい値で突然0に低下することがわかります。
その理由はLASSO回帰方程式に関連しており、詳しく説明しません。
LASSO回帰の可変係数を出力します。
print(lcv.coef_)
# 出力結果
[0.0.0.027894890.26549855]
最初の2つの変数、つまり年齢と収入が除外されていることがわかります。
結果がLingRegressionと異なるのはなぜですか? ? ?
Recommended Posts