Use python to achieve stepwise regression

The basic idea of stepwise regression is to introduce variables into the model one by one. After each explanatory variable is introduced, an F test is performed, and the selected explanatory variables are tested one by one. When the originally introduced explanatory variables are due to the subsequent explanatory variables When the introduction becomes no longer significant, it is deleted. To ensure that only significant variables are included in the regression equation before each new variable is introduced. This is an iterative process until neither significant explanatory variables are selected into the regression equation, and no insignificant explanatory variables are eliminated from the regression equation. To ensure that the final set of explanatory variables is optimal.

The stepwise regression in this example is changed. The t-test is not performed on the variables that have been introduced, and only whether the variables are introduced and excluded. The "double test" stepwise regression, referred to as stepwise regression. Example link: (the original link has expired), 4 independent variables, 1 dependent variable. Mathematics reasoning will not be carried out below, and the calculation process will be explained. For those who do not understand the mathematical theory, please refer to "Modern Medium and Long-term Hydrological Forecasting Methods and Applications" Tang Chengyou, Guan Xuewen, Zhang Shiming; Thesis "Stepwise regression model in dam prediction Application in "Wang Xiaolei, etc.;

Stepwise regression calculation steps:

Calculate the zeroth step augmentation matrix. The zeroth step augmented matrix is composed of the correlation coefficient between the predictor and the predicted object.
Introduction factor. On the basis of the augmented matrix, calculate the variance contribution of each factor, select the factor corresponding to the largest variance contribution among the factors that have not entered the equation, calculate the variance ratio of the factor, and check the F distribution table to determine whether the factor is introduced into the equation.
Elimination factor. Calculate the variance contribution of the factor introduced in the equation at this time, select the factor with the smallest variance contribution, calculate the variance ratio of the factor, and check the F distribution table to determine whether the factor is removed from the equation.
Matrix transformation. The zero-step matrix is transformed according to the factor number of the introduced equation, and the transformed matrix is again subjected to the steps of introducing factors and eliminating factors until no factors can be introduced and no factors can be eliminated, and the stepwise regression analysis calculation is terminated.

**a. The following code implements the subroutine for reading the data, calculating the correlation coefficient and generating the zeroth step augmented matrix. **

Note: The pandas library reads the csv data structure as a DataFrame structure, which is converted to an (n-dimension array, ndarray) array in numpy for calculation

import numpy as np
import pandas as pd
# Data read
# Use pandas to read csv, the data read is a DataFrame object
data = pd.read_csv('sn.csv')
# Convert DataFrame object to array,The last column of the array is the forecast object
data= data.values.copy()
# print(data)
 
# Calculate regression coefficients, parameters
def get_regre_coef(X,Y):
 S_xy=0
 S_xx=0
 S_yy=0
 # Calculate the mean value of forecast factors and forecast objects
 X_mean = np.mean(X)
 Y_mean = np.mean(Y)for i inrange(len(X)):
 S_xy +=(X[i]- X_mean)*(Y[i]- Y_mean)
 S_xx +=pow(X[i]- X_mean,2)
 S_yy +=pow(Y[i]- Y_mean,2)return S_xy/pow(S_xx*S_yy,0.5)
# Construct the original augmented matrix
def get_original_matrix():
 # Create an array to store correlation coefficients,data.a few lines of shape(dimension)Several columns, the result is represented by a tuple
 # print(data.shape[1])
 col=data.shape[1]
 # print(col)
 r=np.ones((col,col))#np.The ones parameter is a tuple(tuple)
 # print(np.ones((col,col)))
 # for row in data.T:#Using array iteration, you can only iterate the rows, iterate the transposed array, and then transpose the result is equivalent to iterating each column
 # print(row.T)for i inrange(col):for j inrange(col):
  r[i,j]=get_regre_coef(data[:,i],data[:,j])return r

**b. The second part is mainly to calculate the tolerance contribution and variance ratio. **

def get_vari_contri(r):
 col = data.shape[1]
 # Create a matrix to store variance contribution values
 v=np.ones((1,col-1))
 # print(v)for i inrange(col-1):
 # v[0,i]=pow(r[i,col-1],2)/r[i,i]
 v[0, i]=pow(r[i, col -1],2)/ r[i, i]return v
# Choose whether the factor enters the equation,
# Parameter description: r is the augmented matrix, v is the variance contribution value, k is the subscript of the factor with the largest variance contribution value,p is the number of factors currently entering the equation
def select_factor(r,v,k,p):
 row=data.shape[0]#Sample size
 col=data.shape[1]-1#Number of predictors
 # Calculate variance ratio
 f=(row-p-2)*v[0,k-1]/(r[col,col]-v[0,k-1])
 # print(calc_vari_contri(r))return f

c. The third part calls the defined function to calculate the variance contribution value

# Calculate the zeroth step augmentation matrix
r=get_original_matrix()
# print(r)
# Calculate variance contribution value
v=get_vari_contri(r)print(v)
# Calculate variance ratio

Calculation results:

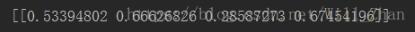
There is no subroutine that judges the largest contribution to the variance, because in other calculations, I also need the specific physical meaning of the variables, so I can’t simply determine the choice of variables by calculation. Here we see that the fourth variable contributes the most to the square check

# # Calculate variance ratio
# print(data.shape[0])
f=select_factor(r,v,4,0)print(f)
####### Output##########
22.79852020138227

Calculate the variance ratio of the fourth predictor (pasted in the code), and check the F distribution table 3.280 for comparison, 22.8 3.28, and introduce the fourth predictor. (The calculation of excluding chairs is not performed for the first three times)

**d. The fourth part performs matrix transformation. **

# Stepwise regression analysis and calculation
# Calculate the element value of each part of the augmented matrix by matrix conversion formula
def convert_matrix(r,k):
 col=data.shape[1]
 k=k-1#Start counting from row zero
 # The element list in row k does not belong to the element in column k
 r1 = np.ones((col, col)) # np.The ones parameter is a tuple(tuple)for i inrange(col):for j inrange(col):if(i==k and j!=k):
  r1[i,j]=r[k,j]/r[k,k]elif(i!=k and j!=k):
  r1[i,j]=r[i,j]-r[i,k]*r[k,j]/r[k,k]elif(i!= k and j== k):
  r1[i,j]=-r[i,k]/r[k,k]else:
  r1[i,j]=1/r[k,k]return r1

e. After performing the matrix transformation, cycle the above steps to introduce and remove factors

Calculate the variance contribution of each factor again

The first three variance factors that are not introduced into the equation are sorted, and the variance contribution of the first factor is obtained. The F-test value of the first predictor is calculated, and the first predictor is introduced into the equation if it is greater than the critical value.

# Matrix conversion, calculate the first step matrix
r=convert_matrix(r,4)
# print(r)
# Calculate the first step variance contribution value
v=get_vari_contri(r)
# print(v)
f=select_factor(r,v,1,1)print(f)
######### Output#####
108.22390933074443

Perform matrix transformation and calculate variance contribution

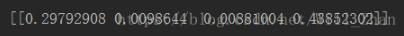
It can be seen that the factors 2 and 3 of the equation have not been introduced, and the factor 2 that contributes the greater variance is factor 2. The f-test value of factor 2 is calculated to be 5.026 3.28, so predict factor 2 is introduced.

f=select_factor(r,v,2,2)print(f)
########## Output#########
5.025864648951804

Continue matrix transformation and calculate variance contribution

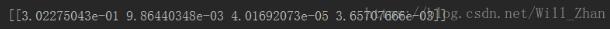
In this step, we need to consider the elimination factor. It can be known that there is variance contribution. Among the factors that have been introduced into the equation, the smallest variance contribution is factor 4. The imported f-test value of factor 3 is calculated as 0.0183.

The f test value of factor 4 is 1.863, which is less than 3.28 (check the F distribution table). Factor 3 cannot be introduced, and factor 4 needs to be eliminated. At this time, the number of factors introduced in the equation is 2

# Choose whether to exclude factors,
# Parameter description: r is the augmented matrix, v is the variance contribution value, k is the subscript of the factor with the largest variance contribution value,t is the number of factors currently entering the equation
def delete_factor(r,v,k,t):
 row = data.shape[0] #Sample size
 col = data.shape[1]-1 #Number of predictors
 # Calculate variance ratio
 f =(row - t -1)* v[0, k -1]/ r[col, col]
 # print(calc_vari_contri(r))return f
# Factor 3 import test value 0.018233473487350636
f=select_factor(r,v,3,3)print(f)
# Factor 4 elimination test value 1.863262422188088
f=delete_factor(r,v,4,3)print(f)

Transform the matrix here and calculate the variance contribution

, The introduced factors (factors 1 and 2) have the smallest contribution to the variance of factor 1, and the largest contribution to the introduction of factor variance is factor 4. Calculate the imported f-test value and eliminate the f-test value of the two

# Factor 4 imported test value 1.8632624221880876, less than 3.28 Cannot be introduced
f=select_factor(r,v,4,2)print(f)
# Factor 1 rejection test value 146.52265486251397,Greater than 3.28 can not be removed
f=delete_factor(r,v,1,2)print(f)

Variables cannot be eliminated or introduced, and the calculation of stepwise regression is stopped at this time. The factors introduced into the equation are predictor 1 and predictor 2, with the help of the multiple regression written in the previous blog. Multivariate regression is performed on the predictor and forecast object entered into the equation. Output the prediction results of multiple regression, once as a constant term, the prediction coefficient of the first factor, and the prediction coefficient of the second factor.

# Factor 1 and Factor 2 enter the equation
# Perform multiple regression on the predictors entered into the equation
# regs=LinearRegression()
X=data[:,0:2]
Y=data[:,4]
X=np.mat(np.c_[np.ones(X.shape[0]),X])#Add constant coefficients to the coefficient matrix
Y=np.mat(Y)#Convert array to matrix
# print(X)
B=np.linalg.inv(X.T*X)*(X.T)*(Y.T)print(B.T)#Output coefficient,The first term is a constant term, the others are regression coefficients
### Output##
#[[52.577348881.468305740.66225049]]

The above article using python to achieve gradual regression is all the content shared by the editor, I hope to give you a reference.