pythonバックトラッキングテンプレートの詳細な説明

バックトラックとは

バックトラッキング方式（探索およびバックトラッキング方式）は、ヒューリスティック方式とも呼ばれる最適な検索方式の一種であり、最適な条件に従って前方に検索して目標を達成します。しかし、あるステップに到達すると、元の選択がうまくいかなかったり、目標が達成されなかったりするので、1つのステップに戻ってもう一度選択します。この戻ると戻るの手法は、バックトラッキング方法であり、バックトラッキング条件を満たす特定の状態のポイントです。これは「バックトラックポイント」と呼ばれます。

繰り返される要素のない完全な配置

すべての要素が異なるリストがある場合、リスト要素の完全な配置を返す必要があります。

n = len（list）とすると、この問題はn-aryツリーと見なすことができます。このツリーでdfsを実行します。この問題のバックトラッキングポイントは、深さ（つまり、一時リストの長さ）です。nの場合、バックトラッキングの条件は、現在の要素がtemplistに表示されます。

バックトラックと再帰：

バックトラックは一種の考えであり、再帰は形式です

classSolution(object):

 # rtlistはすべての戻り値すべての順列を格納するために使用され、templistは各順列を生成するために使用されます
 def backtrack(self,rtlist,templist,nums):if(len(templist)==len(nums)):
  rtlist.append(templist[:])else:for i in nums:if(i in templist): #現在の配置にすでにiがある場合は、続行します。これは、ブランチ制限に相当します。つまり、現在のノードサブツリーは検索されません。
   continue
  templist.append(i)
  self.backtrack(rtlist,templist,nums)
  templist.pop() #終了要素をnumsの次の値に置き換え、次のサブツリーをトラバースします

 def permute(self,nums):
 rtlist =[]
 templist =[]
 self.backtrack(rtlist,templist,nums)return rtlist

nums = [1,2,3]の場合のツリー構造：

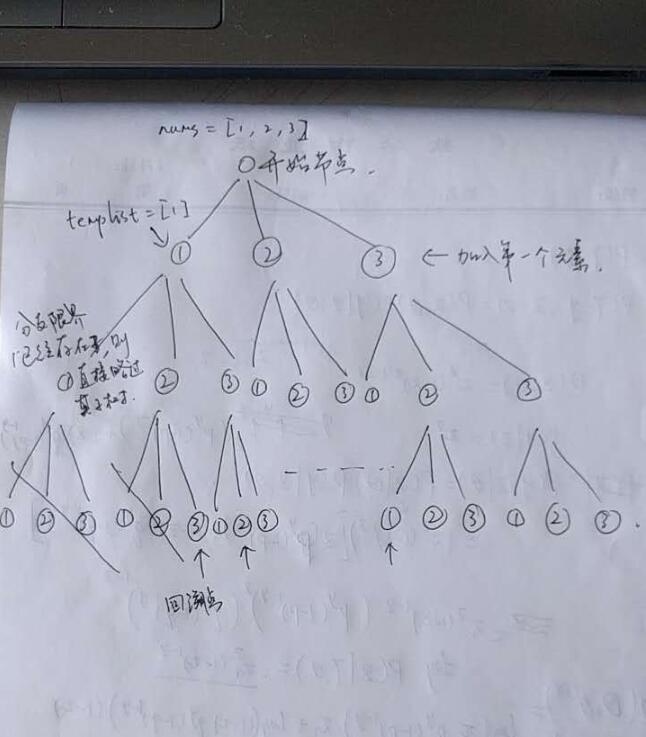
重要なのは、分岐制限とバックトラックポイントを決定することです。

ここに問題があります。再帰するたびにnumsから新しく追加された要素を削除することは可能ですか？実際、リストの操作には一定の時間がかかるため、時間の複雑さはそれほど軽減されません。ソリューションには分岐と境界があるため、時間の複雑さはそれほど悪くありません。

繰り返される要素はすべて配置されます

この問題と上記の問題の違いは、主に分岐と境界の違いです。繰り返される要素をバックトラッキング条件として使用することはできません。そうしないと、すべてが満たされません。

ここでは、カウンターを使用して各要素の出現回数をnumsで記録し、現在の要素が回数を超えた場合に返す必要がありますが、同じ配置が複数回表示される可能性があるという別の問題があります。ここでの解決策は、同じレイヤーで重複する要素を許可しないことです。、2つの解決策があります。1つは個別の配列を直接渡すことであり、もう1つはコレクションを使用して現在のレイヤーの使用済み要素を記録することです。

最初の方法：

from collections import Counter

classSolution(object):

 def backtrack(self, rtlist, tmplist, counter, nums, length):iflen(tmplist)== length:#バックトラックポイント
  rtlist.append(tmplist[:])else:for i in nums:#水平トラバーサル
  if counter[i]==0:#分岐してバインド
   continue

  counter[i]-=1
  tmplist.append(i)
  self.backtrack(rtlist, tmplist, counter, nums, length)#垂直トラバーサル
  counter[i]+=1
  tmplist.pop()

 def permuteUnique(self, nums):

 rtlist, tmplist, counter =[],[],Counter(nums)
 length =len(nums)
 self.backtrack(rtlist, tmplist, counter,list(set(nums)), length)return rtlist

二番目

from collections import Counter

classSolution(object):

 def backtrack(self, rtlist, tmplist, level, counter, nums):iflen(tmplist)==len(nums):
  rtlist.append(tmplist[:])else:for i in nums:if i in level or counter[i]==0:continue

  counter[i]-=1

  tmplist.append(i)
  level.add(i)
  self.backtrack(rtlist, tmplist,set(), counter, nums)

  counter[i]+=1
  tmplist.pop()

 def permuteUnique(self, nums):if not nums:return[]
 rtlist, tmplist, level, counter =[],[],set(),Counter(nums)
 self.backtrack(rtlist, tmplist, level, counter, nums)return rtlist

"="は変数のポイントしか変更できないため、 "="を使用して親関数の変数を変更することはできません。親関数の変数を変更するには、メモリ内で直接変更する必要があります。たとえば、変数をコンテナに入れると、変数のメモリアドレスを直接見つけることができます。通常、container.method（）を使用します。

たとえば、上記のプログラムで、バックトラッキングポイントでカウンターを復元する場合、counter = Counter（nums）を使用することはできませんが、counter [key]を1つずつ変更する必要があります。

総括する

バックトラッキングメソッドは、実際には元の問題をツリーと見なします。このノードのサブツリーをトラバースする代わりに、ツリーをトラバースして不可能な場所に戻り、要件が満たされたときに戻ります。

したがって、バックトラッキング方法では、適切な分岐とバインド（重要）および戻り条件を見つけることが重要です。

詳細については、を参照してください

マルチフォークツリーのトラバーサル方法：
def travel(root):
ルートをトラバースする
現在のレイヤーのすべてのノードのsubtree_rootの場合：
　　travel(subtree_root)

の場合、第1層のすべてのノードが実行され、すべてのノードのすべてのサブツリーが実行されるため、トラバーサルを完了することができます。

上記のpythonバックトラッキングメソッドテンプレートの詳細な説明は、エディターによって共有されるすべてのコンテンツです。参照を提供したいと思います。