Python implementation of intersection and IOU tutorial

Intersection-over-Union (IoU), a concept used in target detection, is the overlap rate between the generated candidate bound and the ground truth bound, that is, their intersection and union. The ratio of the set. The ideal situation is complete overlap, that is, the ratio is 1.

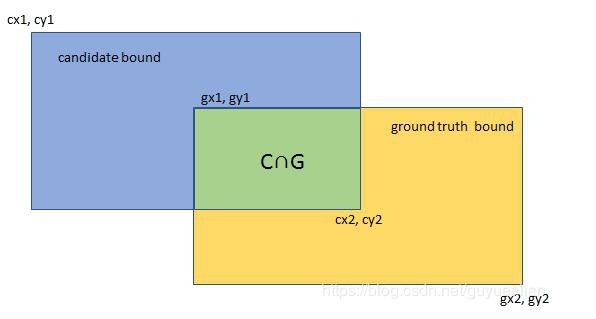
**Calculation formula: **

**Python implementation code: **

def cal_iou(box1, box2):"""
 : param box1:=[xmin1, ymin1, xmax1, ymax1]:param box2:=[xmin2, ymin2, xmax2, ymax2]:return:"""
 xmin1, ymin1, xmax1, ymax1 = box1
 xmin2, ymin2, xmax2, ymax2 = box2
 # Calculate the area of each rectangle
 s1 =(xmax1 - xmin1)*(ymax1 - ymin1) #Area of C
 s2 =(xmax2 - xmin2)*(ymax2 - ymin2) #G area
 
 # Calculate intersecting rectangle
 xmin =max(xmin1, xmin2)
 ymin =max(ymin1, ymin2)
 xmax =min(xmax1, xmax2)
 ymax =min(ymax1, ymax2)
 
 w =max(0, xmax - xmin)
 h =max(0, ymax - ymin)
 area = w * h #C∩G area
 iou = area /(s1 + s2 - area)return iou

# - *- coding: utf-8-*-"""
 @ Project: IOU
 @ File : IOU.py
 @ Author : panjq
 @ E-mail : [email protected]
 @ Date :2018-10-1410:44:06"""
def calIOU_V1(rec1, rec2):"""
 computing IoU
 : param rec1:(y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2:(y0, x0, y1, x1):return: scala value of IoU
 """
 # Calculate the area of each rectangle
 S_rec1 =(rec1[2]- rec1[0])*(rec1[3]- rec1[1])
 S_rec2 =(rec2[2]- rec2[0])*(rec2[3]- rec2[1])
 
 # computing the sum_area
 sum_area = S_rec1 + S_rec2
 
 # find the each edge of intersect rectangle
 left_line =max(rec1[1], rec2[1])
 right_line =min(rec1[3], rec2[3])
 top_line =max(rec1[0], rec2[0])
 bottom_line =min(rec1[2], rec2[2])
 
 # judge if there is an intersect
 if left_line  = right_line or top_line  = bottom_line:return0else:
 intersect =(right_line - left_line)*(bottom_line - top_line)return intersect/(sum_area - intersect)
 
def calIOU_V2(rec1, rec2):"""
 computing IoU
 : param rec1:(y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2:(y0, x0, y1, x1):return: scala value of IoU
 """
 # cx1 = rec1[0]
 # cy1 = rec1[1]
 # cx2 = rec1[2]
 # cy2 = rec1[3]
 # gx1 = rec2[0]
 # gy1 = rec2[1]
 # gx2 = rec2[2]
 # gy2 = rec2[3]
 cx1,cy1,cx2,cy2=rec1
 gx1,gy1,gx2,gy2=rec2
 # Calculate the area of each rectangle
 S_rec1 =(cx2 - cx1)*(cy2 - cy1) #Area of C
 S_rec2 =(gx2 - gx1)*(gy2 - gy1) #G area
 
 # Calculate intersecting rectangle
 x1 =max(cx1, gx1)
 y1 =max(cy1, gy1)
 x2 =min(cx2, gx2)
 y2 =min(cy2, gy2)
 
 w =max(0, x2 - x1)
 h =max(0, y2 - y1)
 area = w * h #C∩G area
 
 iou = area /(S_rec1 + S_rec2 - area)return iou
 
if __name__=='__main__':
 rect1 =(661,27,679,47)
 # ( top, left, bottom, right)
 rect2 =(662,27,682,47)
 iou1 =calIOU_V1(rect1, rect2)
 iou2 =calIOU_V2(rect1, rect2)print(iou1)print(iou2)

Reference: https://www.zalou.cn/article/184542.htm

Supplementary knowledge: Python calculates the confusion matrix of multi-category, Precision, Recall, f1-score, mIOU and other indicators

Go directly to the code, it's clear at a glance

import os
import numpy as np
from glob import glob
from collections import Counter
 
def cal_confu_matrix(label, predict, class_num):
 confu_list =[]for i inrange(class_num):
 c =Counter(predict[np.where(label == i)])
 single_row =[]for j inrange(class_num):
 single_row.append(c[j])
 confu_list.append(single_row)return np.array(confu_list).astype(np.int32)
 
 
def metrics(confu_mat_total, save_path=None):'''
 : param confu_mat:Total confusion matrix
 backgound: whether to kill the background
 : return:txt write out the confusion matrix, precision，recall，IOU，f-score
 '''
 class_num = confu_mat_total.shape[0]
 confu_mat = confu_mat_total.astype(np.float32)+0.0001
 col_sum = np.sum(confu_mat, axis=1) #Sum by line
 raw_sum = np.sum(confu_mat, axis=0) #Number of each column
 
 ''' Calculate various area ratios to find OA value'''
 oa =0for i inrange(class_num):
 oa = oa + confu_mat[i, i]
 oa = oa / confu_mat.sum()'''Kappa'''
 pe_fz =0for i inrange(class_num):
 pe_fz += col_sum[i]* raw_sum[i]
 pe = pe_fz /(np.sum(confu_mat)* np.sum(confu_mat))
 kappa =(oa - pe)/(1- pe)
 
 # Write confusion matrix into excel
 TP =[] #The number of correct classifications for each category in recognition
 
 for i inrange(class_num):
 TP.append(confu_mat[i, i])
 
 # Calculate f1-score
 TP = np.array(TP)
 FN = col_sum - TP
 FP = raw_sum - TP
 
 # Calculate and write out precision, recall, f1-score，f1-m and mIOU
 
 f1_m =[]
 iou_m =[]for i inrange(class_num):
 # Write f1-score
 f1 = TP[i]*2/(TP[i]*2+ FP[i]+ FN[i])
 f1_m.append(f1)
 iou = TP[i]/(TP[i]+ FP[i]+ FN[i])
 iou_m.append(iou)
 
 f1_m = np.array(f1_m)
 iou_m = np.array(iou_m)if save_path is not None:withopen(save_path +'accuracy.txt','w')as f:
 f.write('OA:\t%.4f\n'%(oa*100))
 f.write('kappa:\t%.4f\n'%(kappa*100))
 f.write('mf1-score:\t%.4f\n'%(np.mean(f1_m)*100))
 f.write('mIou:\t%.4f\n'%(np.mean(iou_m)*100))
 
 # Write precision
 f.write('precision:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(TP[i]/raw_sum[i])*100))
 f.write('\n')
 
 # Write recall
 f.write('recall:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(TP[i]/ col_sum[i])*100))
 f.write('\n')
 
 # Write f1-score
 f.write('f1-score:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(f1_m[i])*100))
 f.write('\n')
 
 # Write out IOU
 f.write('Iou:\n')for i inrange(class_num):
 f.write('%.4f\t'%(float(iou_m[i])*100))
 f.write('\n')

The above python implementation cross-combination IOU tutorial is all the content shared by the editor. I hope to give you a reference.