Detailed explanation of python backtracking template

What is backtracking

Backtracking method (exploration and backtracking method) is a kind of optimal search method, also known as heuristic method, which searches forward according to the optimal conditions to achieve the goal. But when you reach a certain step, you find that the original choice is not good or the goal is not achieved, so you go back one step and choose again. This technique of going back and going again is the backtracking method, and the point of a certain state that satisfies the backtracking condition This is called the "backtrack point."

Full arrangement of no repeated elements

Given a list with all elements different, it is required to return the full arrangement of the list elements.

Suppose n = len(list), then this problem can be considered as an n-ary tree. Perform dfs on this tree. The backtracking point in this problem is the depth (that is, the length of the templist). When n, the condition for backtracking is that the current element has been Appeared in the templist.

**Backtracking and recursion: **

Backtracking is a kind of thought, recursion is a form

classSolution(object):

 # rtlist is used to store all return all permutations, templist is used to generate each permutation
 def backtrack(self,rtlist,templist,nums):if(len(templist)==len(nums)):
  rtlist.append(templist[:])else:for i in nums:if(i in templist): #If there is already i in the current arrangement, continue, which is equivalent to the branch limit, that is, the subtree of the current node is not searched
   continue
  templist.append(i)
  self.backtrack(rtlist,templist,nums)
  templist.pop() #Replace the ending element with the next value in nums, and traverse the next subtree

 def permute(self,nums):
 rtlist =[]
 templist =[]
 self.backtrack(rtlist,templist,nums)return rtlist

Tree structure when nums=[1,2,3]:

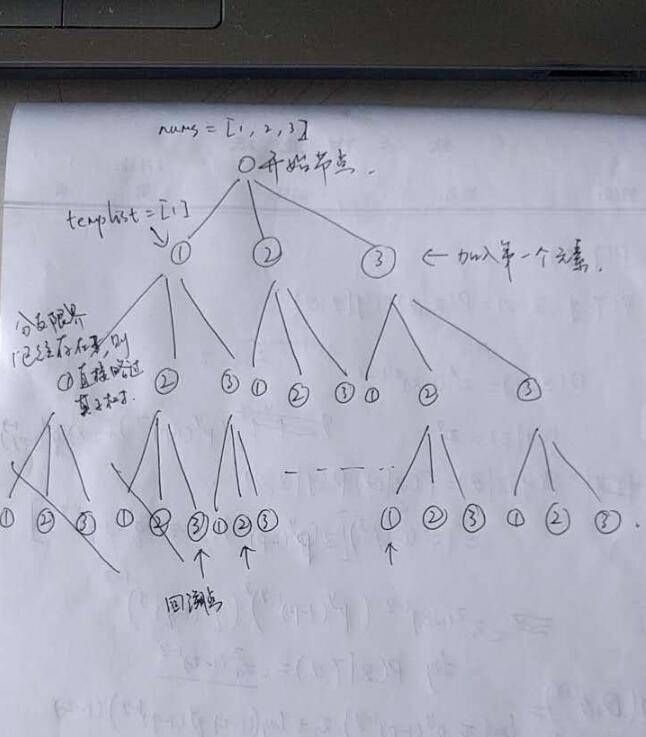
The key is to determine the branch limit and backtracking point.

There is a problem here. Is it possible to delete the newly added element from nums every time you recurse? In fact, the time complexity will not be reduced too much, because it takes a certain amount of time to operate on the list. Because there are branch and bounds in the solution, the time complexity is not too bad.

Repeated elements are all arranged

The difference between this problem and the above is mainly the difference in branch and bounds. Repeated elements cannot be used as the backtracking condition, otherwise all will not be met.

Here we should use a counter to record the number of occurrences of each element in nums, and return if the current element exceeds the number of times, but there is another problem here is that the same arrangement may appear multiple times. The solution here is to not allow duplicate elements in the same layer , There are two solutions, one is to pass in the distinct array directly, and the other is to use a collection to record the used elements of the current layer.

the first method:

from collections import Counter

classSolution(object):

 def backtrack(self, rtlist, tmplist, counter, nums, length):iflen(tmplist)== length:#Backtracking point
  rtlist.append(tmplist[:])else:for i in nums:#Horizontal traversal
  if counter[i]==0:#Branch and bound
   continue

  counter[i]-=1
  tmplist.append(i)
  self.backtrack(rtlist, tmplist, counter, nums, length)#Vertical traversal
  counter[i]+=1
  tmplist.pop()

 def permuteUnique(self, nums):

 rtlist, tmplist, counter =[],[],Counter(nums)
 length =len(nums)
 self.backtrack(rtlist, tmplist, counter,list(set(nums)), length)return rtlist

The second

from collections import Counter

classSolution(object):

 def backtrack(self, rtlist, tmplist, level, counter, nums):iflen(tmplist)==len(nums):
  rtlist.append(tmplist[:])else:for i in nums:if i in level or counter[i]==0:continue

  counter[i]-=1

  tmplist.append(i)
  level.add(i)
  self.backtrack(rtlist, tmplist,set(), counter, nums)

  counter[i]+=1
  tmplist.pop()

 def permuteUnique(self, nums):if not nums:return[]
 rtlist, tmplist, level, counter =[],[],set(),Counter(nums)
 self.backtrack(rtlist, tmplist, level, counter, nums)return rtlist

During recursion, you cannot use "=" to modify the variable of the parent function, because "=" can only change the point of the variable. To modify the variable of the parent function, you must modify it directly in the memory. For example, you can directly find the memory address of the variable when you put it in a container. Usually use container.method().

For example, in the above program, if we want to restore the counter at the backtracking point, we cannot use counter = Counter(nums), but we should modify counter[key] one by one.

to sum up

The backtracking method is actually to consider the original problem as a tree. We traverse the tree and return where it is impossible, instead of traversing the subtree of this node, and return when the requirements are met.

So in the backtracking method, the key is to find a reasonable branch and bound (important) and return conditions.

For more please refer to

Traversal method of multi-fork tree:
def travel(root):
Traverse root
for subtree_root in all nodes of the current layer:
　　travel(subtree_root)

In for, all nodes of the first layer are executed travel, and because all subtrees of all nodes are executed travel, the traversal can be completed.

The above detailed explanation of the python backtracking method template is all the content shared by the editor. I hope to give you a reference.