Python calculation of information entropy example

The formula for calculating information entropy: n is the number of categories, p(xi) is the probability of the i-th category

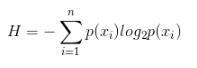
Assuming that the data set has m rows, that is, m samples, and the last column of each row is the label of the sample, the code for calculating the information entropy of the data set is as follows:

from math import log
 
def calcShannonEnt(dataSet):
 numEntries =len(dataSet) #Number of samples
 labelCounts ={} #The frequency of each category in the data set
 for featVec in dataSet: #Sample for each row
 currentLabel = featVec[-1] #Label of the sample
 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel]=0
 labelCounts[currentLabel]+=1 
 shannonEnt =0.0for key in labelCounts:
 prob =float(labelCounts[key])/numEntries #Calculate p(xi)
 shannonEnt -= prob *log(prob,2) # log base 2return shannonEnt

Supplementary knowledge: python realizes information entropy, conditional entropy, information gain, Gini coefficient

I won’t say much nonsense, everyone should just look at the code~

import pandas as pd
import numpy as np
import math
## Calculate information entropy
def getEntropy(s):
 # Find the number of occurrences of different values
 if not isinstance(s, pd.core.series.Series):
 s = pd.Series(s)
 prt_ary = pd.groupby(s , by = s).count().values /float(len(s))return-(np.log2(prt_ary)* prt_ary).sum()
## Calculate conditional entropy:Conditional entropy of s2 under condition s1
def getCondEntropy(s1 , s2):
 d =dict()for i inlist(range(len(s1))):
 d[s1[i]]= d.get(s1[i],[])+[s2[i]]returnsum([getEntropy(d[k])*len(d[k])/float(len(s1))for k in d])

## Calculate information gain
def getEntropyGain(s1, s2):returngetEntropy(s2)-getCondEntropy(s1, s2)

## Calculate gain rate
def getEntropyGainRadio(s1, s2):returngetEntropyGain(s1, s2)/getEntropy(s2)

## Measuring the correlation of discrete values
import math
def getDiscreteCorr(s1, s2):returngetEntropyGain(s1,s2)/ math.sqrt(getEntropy(s1)*getEntropy(s2))

# ######## Calculate the probability sum of squares
def getProbSS(s):if not isinstance(s, pd.core.series.Series):
 s = pd.Series(s)
 prt_ary = pd.groupby(s, by = s).count().values /float(len(s))returnsum(prt_ary **2)
######## Calculate the Gini coefficient
def getGini(s1, s2):
 d =dict()for i inlist(range(len(s1))):
 d[s1[i]]= d.get(s1[i],[])+[s2[i]]return1-sum([getProbSS(d[k])*len(d[k])/float(len(s1))for k in d])
## Calculate the correlation coefficient for discrete variables and draw a heat map,Returns the correlation matrix
def DiscreteCorr(C_data):
 ## For discrete variables(C_data)Calculate the correlation coefficient
 C_data_column_names = C_data.columns.tolist()
 ## Store C_matrix of data correlation coefficients
 import numpy as np
 dp_corr_mat = np.zeros([len(C_data_column_names),len(C_data_column_names)])for i inrange(len(C_data_column_names)):for j inrange(len(C_data_column_names)):
  # Calculate the correlation coefficient between two attributes
  temp_corr =getDiscreteCorr(C_data.iloc[:,i], C_data.iloc[:,j])
  dp_corr_mat[i][j]= temp_corr
 # Draw the correlation coefficient graph
 fig = plt.figure()
 fig.add_subplot(2,2,1)
 sns.heatmap(dp_corr_mat ,vmin=-1, vmax=1, cmap= sns.color_palette('RdBu', n_colors=128), xticklabels= C_data_column_names , yticklabels= C_data_column_names)return pd.DataFrame(dp_corr_mat)if __name__ =="__main__":
 s1 = pd.Series(['X1','X1','X2','X2','X2','X2'])
 s2 = pd.Series(['Y1','Y1','Y1','Y2','Y2','Y2'])print('CondEntropy:',getCondEntropy(s1, s2))print('EntropyGain:',getEntropyGain(s1, s2))print('EntropyGainRadio',getEntropyGainRadio(s1 , s2))print('DiscreteCorr:',getDiscreteCorr(s1, s1))print('Gini',getGini(s1, s2))

The above Python information entropy calculation example is all the content shared by the editor, I hope to give you a reference.